SEBA Class 7 Maths Chapter 7 Congruence of Triangles Solutions | Exercises 7.1 & 7.2 | Assam English Medium | SCERT Assam | QR Code: D5K9S2

SEBA Class 7 Maths Chapter 7 Congruence of Triangles Solutions | SCERT Assam | Exercises 7.1 & 7.2

Find SEBA Class 7 Maths Chapter 7 Congruence of Triangles Solutions for Exercises 7.1 and 7.2 in English Medium, following the SCERT Assam syllabus. Learn about congruence rules (SSS, SAS, ASA, RHS), properties of congruent triangles, and problem-solving techniques with step-by-step solutions. Perfect for SEBA students preparing for exams and understanding the concepts clearly. QR Code: D5K9S2.

📚 Get Complete SEBA Class 7 Maths Solutions – Access step-by-step solutions for all chapters as per the SCERT Assam syllabus.

➡ Click here for full subject solutions

Congruence of Triangles

Exercise – 7.1

1. Measures of sides of pairs of triangles are given in figure below. Show that the pairs are congruent. Mention the congruence criteria.

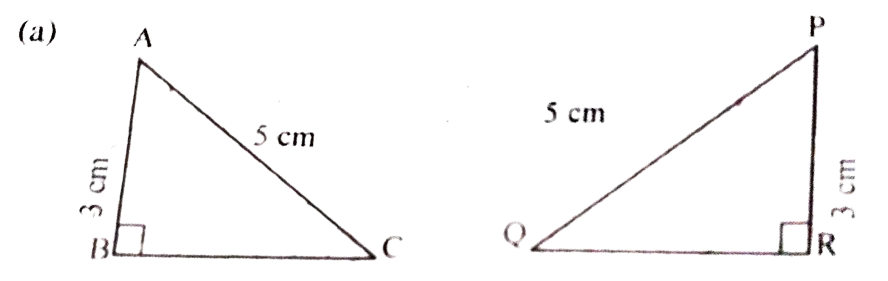
Ans: RHS.

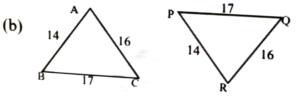
Ans: SSS.

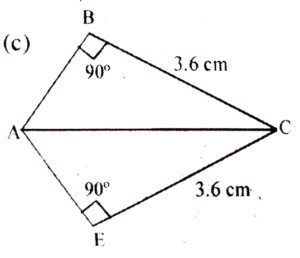
Ans: RHS.

Ans: RGS.

(e)

Ans: SSS.

Ans: SAS.

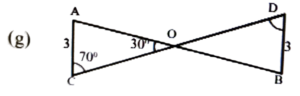
Ans: AAS.

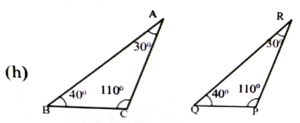
Ans: AAS or ASA

2. In fig (i)

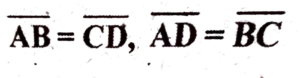
Prove that ∆ADC ≌ ∆CВА

Ans: Given:

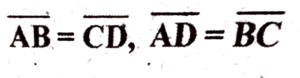
To prove: ∆ADC ≌ ∆CВА

Proof: From ∆ADC and ∆CВА

Proof that ∆PRQ ≌ ∆PSQ

Ans: From given ∆PRQ and ∆PSQ

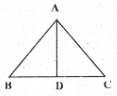
4. In the figure below ∆ABC is a Isosceles triangle, where

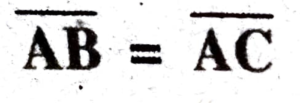and is its median. Prove that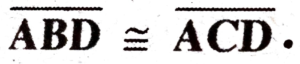

Ans: In given figure ∆ABC

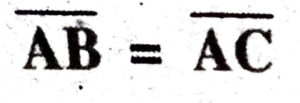and

5. ABC is a Isosceles triangle with and AD is its altitude.

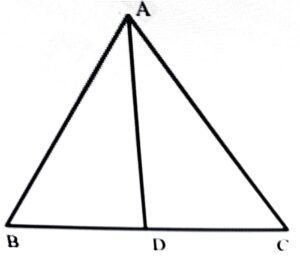
(i) Write down three equal parts of ∆ADB and ∆ADC.

Ans: Three equal parts of ∆ADB and ∆ADC are ∠A = ∠C, AD = AD (Common side), BD = CD.

(ii) Is AABD = AADC? Give reason.

Ans: Yes, ∆ADB = ∆ADC because is a median.

(iii) Is ∠B = ∠C?

Ans: ∠B = ∠C, because ∆ADB = ∆ADC

(iv) 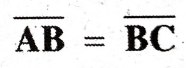give reasons?

Ans:

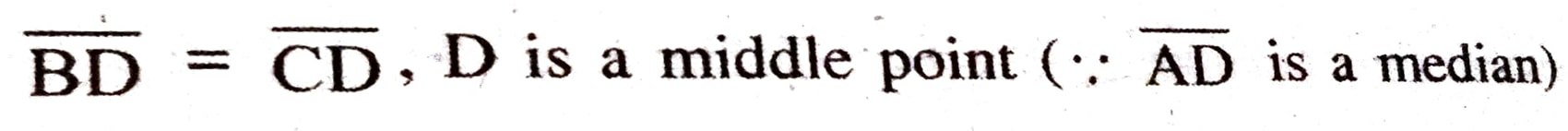
6. In ∆ ABC, ∠A = 30° ∠C = 110° and in ∆ PQR, ∠P = 30°, ∠R = 110°, Is ∆ ABC ≅ ∆PQR?

Ans: Yes, ∆ ABC = ∆PQR, because ∠A = ∠P ∠C = 4 ∠R and (According to A-S-A Property).

7. In the figure bisects ∠A also, in ∆АВС, show that the angles opposite to equal sides are equal.

Ans:

∆ ABD = ∆ADC [According to S-S-S and S – A -: Property] ∠B = ∠C

8. In ∆ABC, ∠B = ∠C, and are bisectors o ∠B and ∠C respectively. Prove that

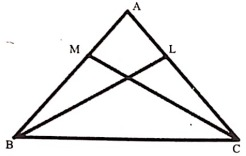
Ans: Given: In ∆ABC, ∠B = ∠C, and are bisectors of ∠B and C respectively.

Prove that:

Proof: From ∆BCM and ∆BCL, ∠B = ∠C, 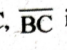is a common side, .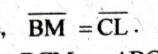

∴ ВСМ = ∆BCL (According to S-A-S Property)

∴ (Proved)

9. If the mid point M of the base is equidistant from the other two sides of a triangle ∆ABC then show that the triangle is isosceles.

Ans:

Given: If the mid point M of the base is equidistant from the other two sides of a ∆ABC

To show:

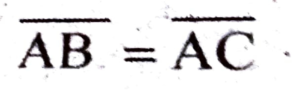
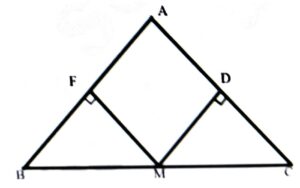
Proof: From ∆BFM and ∆DCM, (∴ M is the mid point of BC)

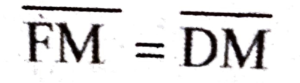(Given)

<BFM = CDM = 90°

∴ ∆BFM = ∆DCM

∴ ∠B = ∠C

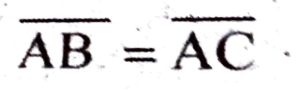∴ (Showed)

10. In fig., Write down three equal parts of ∆ABC and ∆DAB. Show that-

(i) ∆АВС ≅ ∆BAD

Ans: In fig, ans AB = AB (Common side), and DA = CB, ∠A = ∠B

∴ ∆ABC = ∆BAD [According to S-A-S Property) [Showed]

11. In the given figure BD and CE are two altitudes of ΔABC such that BD = CE.

(i) Write three equal parts of ΔBCD and ΔВСЕ

(ii) Is ΔCBD ≌ ΔBCE?

(iii) Is ∠DCB ≌ ∠EBC? If not, why?

Ans: In the given figure BD and CE are two altitudes of ∆ABC such that BD = CE.

(i) Three equal parts of ∆CBD and ∆BCE are ∠B = ∠C, ∠BEC = ∠BDC and BC = BC (Common side)

(ii) ∆CBD ≌ ∆BCE [According to A-A-S property]

(iii) ∠DCB = ∠EBC [∴ BD= CE]

12. In the given figure and . Show that, ∆ABC ≌ ∆CDA.

Ans:

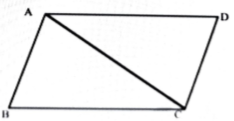
In the given figure and

Το show: ΔABC ≌ ∆CDA

Proof: From ∆ABC and ∆CDA, and (Common side).

∆ ABC ≌ ∆CDA (According to S-S-S Property.)

Exercise – 7.2

Find out the correct statements of the following questions:

1. If in ∆ABC and ∆PQR, AB = 4 cm BC = 5 cm AC = 6 cm, PQ = 4 cm OR = 5 cm PR = 6 cm then:

(a) ∆ΑΒC ≌ ∆QRP

(b) ∆АВС ≌ ∆PQR

(c) ∆АВС ≌ ∆PRQ

(d) ∆ΑΒC ≌ ∆QPR

Ans: (b) ∆АВС ≌ ∆PQR

2. In ∆ABC, ∠A = 90° and then.

(a) ∠B = ∠C = 60°

(b) ∠B = ∠C = 30°

(c) ∠B = ∠C = 45°

(d) ∠B = ∠B = 50°

Ans: (c) ∠B = ∠C = 45°

3. The measure of each angle of an equilateral triangle-

(a) 60°

(b) 30°

(c) 45°

(d) 40°

Ans: (a) 60°

4. In the figure AB = CD, AD = CB and ∠DAB = ∠BCD then

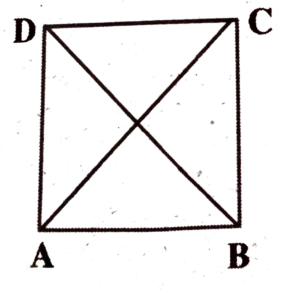
(a) ∆ΑΒC ≌ ∆ADC

(b) ∆АВС ≌ ∆ACD

(c) ∆BAD ≌ ∆DCB

(d) ∆ΑΒC ≌ CAD

Ans: (c) ∆BAD ≌ ∆DCB

5. In ∆ABC and ∆PQR AB = 3.5 cm BC = 7.1cm AC = 5 cm. PQ = 7.1cm QR = 5 cm and PR = 3.5cm Which of the following statements is correct?

(a) ∆АВС ≌ ∆QRP

(b) ∆ΑΒC ≌ ∆PQR

(c) ∆ABC ≌ ∆RPO

(d) ∆ΑΒΟ ≌ ∆OPR

Ans: (c) ∆ABC ≌ ∆RPO

6. In ∆ABC and ∆DEF AB = 7cm BC = 5cm, ∠B = 50° DE = 5cm EF = 7cm ∠E = 50° Under which condition, are the traingles congruent?

(a) SAS.

(b) RHS.

(c) ASA.

(d) SSS.

Ans: (a) SAS.

7. In ∆ABC and ∆PQR ∠B = ∠P = 90° and AB = RP Triangles are congruent if,

(a) AC = RQ

(b) ∠A = ∠P

(c) BC = QR

(d) ∠R = ∠C

Ans: (a) AC = RQ

৪. If ∆AB C cong ∠DEF and ∠A = 50°, ∠E = 85 ° then ∠C = ?

(a) 50°

(b) 45°

(c) 85°

(d) 40°

Ans: (b) 45°

FAQs Sections