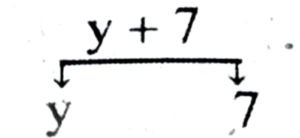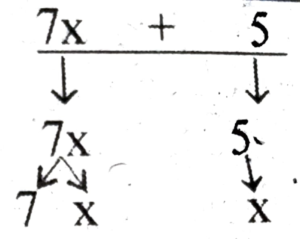SEBA Class 7 Maths Chapter 12 Algebraic Expressions Solutions | SCERT Assam | Exercises 12.1 to 12.4 | QR Code: V1W3R3

SEBA Class 7 Maths Chapter 12 Algebraic Expressions Solutions | SCERT Assam

Get SEBA Class 7 Maths Chapter 12 Algebraic Expressions Solutions for Exercises 12.1, 12.2, 12.3, and 12.4 in English Medium, as per the SCERT Assam syllabus. This chapter covers essential topics like terms, coefficients, polynomials, addition and subtraction of algebraic expressions, and simplifications. Our step-by-step detailed solutions help students understand how to form, solve, and manipulate algebraic expressions with ease.Scan QR Code: V1W3R3 for instant access to solutions.

📚 Get Complete SEBA Class 7 Maths Solutions – Access step-by-step solutions for all chapters as per the SCERT Assam syllabus.

➡ Click here for full subject solutions

Algebraic Expressions

Exercise 12.1

1. Write the algebraic expressions of the following using variable,

constant and arithmetic operation.

(i) Multiply x by x and add 2.

Ans: x × x + 2

= x² + 2

(ii) Sum of a and b.

Ans: a + b

(iii) Subtraction of 7 from x.

Ans: x – 7

(iv) Subtraction of z from Y.

Ans: y – z

(v) Multiplication of y to ‘square of x’ and added to z.

Ans: x²y + z

(vi) Half of the product of x and y.

Ans: 1/2 × xy

(vii) Sum of y and z subtracted from the product of y

Ans: yz – (y + z)

(viii) Addition of z with the quotient of x divided by y

Ans: x/y + z

(ix) Addition of z with three time of x

Ans: 3x + z

(x) Sum of x and 6 is divided by 3.

Ans: (x + 6)/3

(xi) Square of the product of x and 5.

Ans: (x × 5)²

(xii) Multiplication of 5 with the square of x.

Ans: 5x²

2. There are ‘n’ nos of chocolates in each of the following 5 containers –

(i) If two more chocolates are added to each container, total how

many chocolates will be there?

Ans: Total number of chocolates = 5n + 10.

(ii) If n = 10, what will be the total number of chocolate?

Ans: If n = 10 the total number of chocolates = 5 ×10 = 50

3. In the following picture a few balls are arranged in rows and

columns. Express the total no of balls in algebraic expression.

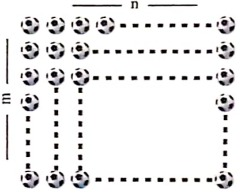
Ans: The total no. of balls in algebraic expression; m x ×n = mn.

4. Identify the term and factors in the following expressions. Show

the terms and factors with the help of a tree diagram.

(a) y + 7

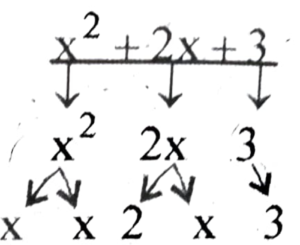
(b) x² + 2x + 3

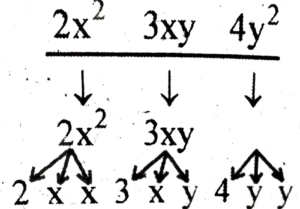
(c) 2x² + 3xy + 4y²

(d) 7x + 5

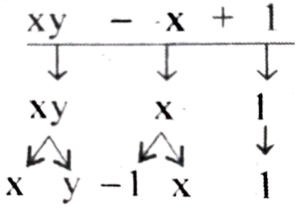
(e) xy – x + 1

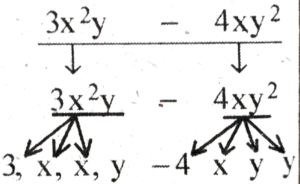
(f) 3x²y – 4xy²

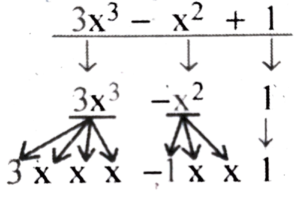
(g) 3x³ – x² + 1

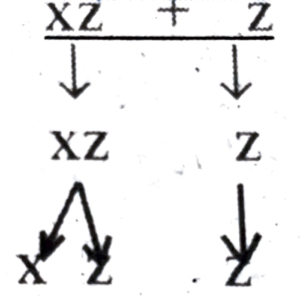
(h) xz + z

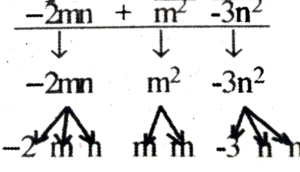
(i) -2mn + m² – 3n²

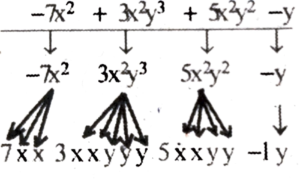
(j) -7x² + 3x²y³ + 5x²y² – y

Ans:

	Expression	Term	Factor	Tree diagram
(a)	Y + 7	Y/7	Y/7
(b)	x² + 2x + 3	x² 2x 3	X, x 2, x 3
(c)	2x² + 3xy + 4y²	2x² 3xy 4y²	2, x, x 3,x,y 4,y,y
(d)	7x + 5	7x 5	7, x 5
(e)	xy – x + 1	X y – x 1	X, y -1, x 1
(f)	3x²y – 4xy²	3x²y – 4xy²	3, x, x, y – 4, x, y, y
(g)	3x³ – x² + 1	3x³ – x² 1	3, x, x, x – 1, x, x 1
(h)	xz + z	xz z	X, z z
(i)	-2mn + m² – 3n²	-2mn m² – 3n²	-2, m, n M, m – 3, n, n
(j)	-7x² + 3x²y³ + 5x²y² – y	-7x² 3x²y³ 5x²y² – y	-7, x, x 3, x, x, y, y, y 5, x, x, y, y -1, y

5. Fill up the following tables:

(a)

	Expression	Term (which is not constant)	Numerical coefficient
(i)	2x + 3y
(ii)	mn + 3
(iii)	2ab – a + b
(iv)	2x²y – 4xy² + 7
(v)	3x³ – 7x² + y

Ans:

	Expression	Term (which is not constant)	Numerical coefficient
(i)	2x + 3y	2x, 3y	2, 3
(ii)	mn + 3	mn	1
(iii)	2ab – a + b	2a, -a, b	2, -1, 1
(iv)	2x²y – 4xy² + 7	2x²y, 4xy²	2, -4
(v)	3x³ – 7x² + y	3x², 7x², y	3, -7,1

(b)

	Expression	Term with factor x	Coefficient of x
(i)	xy³ + 1
(ii)	2xy + y + 1
(iii)	3xy² – xy + x
(iv)	7xz – z
(v)	y – x + 2

Ans:

	Expression	Term with factor x	Coefficient of x
(i)	xy³ + 1	xy³	y³
(ii)	2xy + y + 1	2xy	2y
(iii)	3xy² – xy + x	3xy², -xy, x	3y², -y, 1
(iv)	7xz – z	7xz	7z
(v)	y – x + 2	-x	-1

(c)

	Expression	Term with factor b²	Coefficient of b²
(i)	ab² + 9
(ii)	ab² + a²b + 3a
(iii)	-b³ +3a²b -5b²

Ans:

	Expression	Term with factor b²	Coefficient of b²
(i)	ab² + 9	ab²	a
(ii)	ab² + a²b + 3a	ab²	a
(iii)	-b³ +3a²b -5b²	-5b²	5

6. Classify the following expressions as monomials, binomials and trinomials-

(i) 2x + 3

Ans: Binomial.

(ii) y³

Ans: Monomial.

(iii) 3a²b

Ans: Monomial.

(iv) 3a²b + 5ab² + 3a

Ans: Trinomial.

(v) 2m + 3n

Ans: Binomial.

(vi) x² + x

Ans: Binomial.

(vii) m² + n²

Ans: Binomial.

(viii) 2x² + 3x + 1

Ans: Trinomial.

(ix) xy + y

Ans: Binomial.

(x) 34

Ans: Monomial.

7. (a) Write whether the following pairs of term is like or unlike terms.

(i) -4x, 1/2x

Ans: Like term.

(ii) -5x; 7y

Ans: Unlike term.

(iii) 9, 20

Ans: Like term.

(iv) 2x²y, 3xy²

Ans: Unlike term.

(v) 2xy, 3xz

Ans: Unlike term.

(vi) -7xz, 2xz

Ans: Like term.

(vii) x², x³

Ans: Unlike term.

(viii) x², 2x²

Ans: Like term.

(ix) mn, 3nm

Ans: Like term.

(x) 1/2z, 3/4z

Ans: Like term.

(b) Identify the like terms in the following.

ab², a², xy², y³, 4xy², 7ab², -2x, 5y, xy, 3x, -ab², a²b², 3ab², x³y³, 40x -m²n, 3mn², -m²n, 2a²b², 3y.

Ans: Similar terms to the given terms are:

ab², -ab², 7ab², 3ab²

xy², 4xy²

-2x, 3x, 40x

-m²n, -m²n

a²b², 2a²b²

5y, 3y

Exercise 12.2

1. Rearrange the like terms and simplify.

(i) 2x + 3y – 45 + 6y – 7x + 5

Ans: 2x + 3y – 45 + 6y – 7x + 5

= (2x – 7x) + (3y + 6y) – (45 + 5)

= (2 – 7)x + (3 + 6)y(- 40)

= -5x + 9y – 40

(ii) x² – 2x + y² + 2x² + 4x + y³

Ans: x² – 2x + y² + 2x² + 4x + y³

= (x² + 2x²) + (-2x + 4x) + y² + y³

= (1 + 2)x² + (-2 + 4)x + y² + y³

= 3x² + 2x + y² + y³

(iii) a – (2a – 3b) – b – (3b – 4a)

Ans: a – (2a – 3b) – b – (3b – 4a)

= a – 2a + 3b – b – 3b + 4a

= (a – 2a + 4a) + (3b – b – 3b)

= (1 – 2 + 4)a + (3 – 1 – 3)b

= 3a + (-1)b

= 3a – b

(iv) x²y + 3xy² + y³ – 3x²y + 2xy² – 3y³ + 5

Ans: x²y + 3xy² + y³ – 3x²y + 2xy² – 3y³ + 5

= (x²y + 3xy²) + (3xy² + 2xy²) + (y³ – 3x²) + 5

= (1 – 3)x²y + (3 + 2)xy² + (1 – 3)y³ + 5

= -2x²y + 5xy² – 2y³ + 5

(v) (2z² + 3y + 7) – (3y – 8z² + 1)

Ans: (2z² + 3y + 7) – (3y – 8z² + 1)

= 2z² + 3y + 7 – 3y – 8z² + 1

= (2 + 8)z² + (3 – 3)y + 8

= 10z² + 0 × y + 8

= 10z² + 8

2. Add

(i) 3x²y, -2x²y, 7x²y, 2x²y

Ans: 3x²y, -2x²y, 7x²y, 2x²y

= 3x²y + (-2x²y) + 7x²y + 2x²y

= 3x² – 2x²y + 7x²y + 2x²y

= (3 – 2 + 7 + 2)x²y

= 10x²y

(ii) x + xy, 3xy + x, x – 1

Ans: x + xy, 3xy + x, x – 1

= (x + xy) + (3xy + x)(x – 1)

= x + xy + 3xy + x + x – 1

= (x + x + x) + (xy + 3xy) – 1

= 3x + 4xy – 1

(iii) 2x² + 3xy + y², – 3x² + 5xy + 2y², x² – 8xy – 3y²

Ans: 2x² + 3xy + y², – 3x² + 5xy + 2y², x² – 8xy – 3y²

= (2x² + 3xy + y²) + (-3x² + 5xy + 2y²)(x² – 8xy – 3y²)

= 2x² + 3xy + y² – 3x² + 5xy + 2y² + x² – 8xy – 3y²

= (2x² – 3x² + x²) + (3xy + 5xy – 8xy) + (y² + 2y² – 3y²)

= (2 – 3 + 1)x² + (3 + 5 – 8)xy + (1 + 2 – 3)y²

= 0 × x² + 0 × xy + 0 × y²

= 0

(iv) 3x + 4y, – 7x + 5y + 2, 2x + 5xy + 7

Ans: 3x + 4y, – 7x + 5y + 2, 2x + 5xy + 7

= (3x + 4y) + (-7x + 5y + 2) + (2x + 5xy + 7)

= 3x + 4y – 7x + 5y + 2 + 12x + 5xy + 7

= (3x – 7x + 12x) + (4y + 5y) + 5xy + (2 + 7)

= (3 – 7 + 12)x + (4 + 5)y + 5xy + 9

= 8x + 9y + 5xy + 9

(v) 6xy, 7yx, 3xz, 5yz

Ans: 6xy, 7yx, 3xz, 5yz

= 6xy + 7yx + 3xz + 5yz

= 6xy + (7yz + 5yz) + 3xz

= 6xy + (7 + 5)yz + 3xz

= 6xy + 12yz + 3xz

(vi) 2x² – y² + 5, y² + 3 – x², x² + y² + 1

Ans: 2x² – y² + 5, y² + 3 – x², x² + y² + 1

= (2x² – y² + 5) + (y² + 3 – x²) + (x² + y² + 1)

= (2x² – y² + 5 + y² + 3 – x² + x² + y² + 1)

= (2x² – x² + x²) + (-y² + y² + y²) + (5 + 3 + 1)

= (2 – 1 + 1)x² + (-1 + 1 + 1)y² + 9

= 2x² + y² + 9

(vii) x²y² + xy + 1, -2x²y² + 3xy – 2, 3x²y² – 5xy + x

Ans: x²y² + xy + 1, -2x²y² + 3xy – 2, 3x²y² – 5xy + x

= (x²y² + xy + 1) + (-2x²y² + 3xy – 2) + (3x²y² – 5xy + x)

= x²y² + xy + 1 – 2x²y² + 3xy – 2 + 3x²y² – 5xy + x

= (x²y² – 2x²y² + 3x²y²) + (xy + 1 + 3xy – 5xy) + x + (1 – 2)

= 2x²y² + (-1)xy + x – 1

= 2x²y² + z², z² +1

(viii) 3y² + yz, – y² + 2yz + z², z² + 1

Ans: 3y² + yz, – y² + 2yz + z², z² + 1

= (3y² + yz) + (-y² + 2yz + z²) + (z² + 1)

= 3y² + yz – y² + 2yz + z² + z² + 1

= (3y² – y²) + (yz + 2yz) + (z² + z²) + 1

= (3 – 1)y² + (1 + 2)yz + (1 + 1)z² + 1

= 2y² + 3yz + 2z² + 1

3. Subtract:

(i) -7x²y from 5x²y

Ans: 5x²y – (-7x²y)

= 5x²y + 7x²y

= (5 + 7)x²y

= 12x²y

(ii) 2xy from 7xy

Ans: 7xy – 2xy

= 7xy – 2xy

= (7 – 2)xy

= 5xy

(iii) -x² – 2xy + y² from 2x² + 3xy + 4y²

Ans: 2x² + 3xy + 4y² -( -x² – 2xy + y²)

= (2x² + 3xy + 4y²) – (-x² – 2xy + y²)

= 2x² + 3xy + 4y² + x² – 2xy + y²

= (2x² + x²) + (3xy + 2xy) + (4y² – y²)

= (2 + 1)x² + (3 + 2)xy + (4 – 1)y²

= 3x² + 5xy + 3y²

(iv) -2x²y² + 2xy + 5 from 5x²y² + xy + 7

Ans: 5x²y² + xy + 7 – (-2x²y² + 2xy + 5)

= (5x²y² + xy + 7) – (-2x²y² – 2xy + 5)

= 5x²y² + xy + 7 + 2x²y² – 2xy + 5

= (5x²y² + 2x²y²) + (xy – 2xy) + (7 – 5)

= (5 + 2)x²y² + (1 – 2)xy + 2

= 7x²y² + (-1)xy + 2

= 7x²y² – xy + 2

(v) 2m² – 3m + 1 from 2m + 3n

Ans: 2m + 3n – 2m² – 3m + 1

= (2m + 3n) – (2m² – 3m + 1)

= 2m + 3n – 2m² + 3m – 1

= (2m + 3m) + 3n – 2m² – 1

= (2 + 3)m + 3n – 2m² – 1

= 5m + 3n – 2m² – 1

(vi) 2pq + p² + q² from 6pq – p² – q²

Ans: 6pq – p² – q² – (2pq + p² + q²)

= (6pq – p² – q²) – (2pq + p² + q²)

= 6pq – p² – q² – 2pq + p² + q²

= (6pq – 2pq) + (-p² – q²) + (-p² – q²)

= (6 – 2)pq + (-1 – 1)p² + (-1 – 1)q²

= 4pq + (-2)p² + (-2)q²

= 4pq – 2p² – 2q²

(vii) p² + 1 from 2p – 7

Ans: 2p – 7 – (p² + 1)

= (2p – 7) – (p² + 1)

= (2p – 7) – (p² + 1)

= 2p – 7 – p² – 1

= 2p – p² – (7 + 1)

= 2p – p² – 8

(viii) 4x² + 5x + 3 from 3x² – 2x + 1

Ans: 3x² – 2x + 1 – (-4x² + 5x + 3)

= (3x² – 2x + 1) – (-4x² + 5x + 3)

= 3x² – 2x + 1 + 4x² + 5x + 3

= (3 + 4)x² + (-2 – 5)x + (-2)

= (3x² + 4x²) + (-2x – 5x) + (1 – 3)

= 7x² + (-7)x + (-2)

= 7x² – 7x – 2

4. Sum of two algebraic expressions is 5x² + 2x + 1, if one expression is x² + 5x + 7 find the other.

Ans: Algebraic Sum = 5x² + 2x + 1

= x² + 5x + 7

∴ Other expression = (5x² + 2x + 1) – (x² + 5x + 7)

= 5x² + 2x + 1 – x² + 5x + 7

= (5x² – x²) + (2x – 5x) + (1 – 7)

= (5 – 1)x² + (2 – 5)x + (-6)

= 4x² – 3x – 6

5. To get 7x + 3y + 1 how much needs to be subtracted from 2x

+ 4y + 7.

Ans: ∴ Reqd. expression = (2x + 4y + 7) – (7x + 3y + 1)

= 2x + 4y + 7 – 7x – 3y – 1

= (2x – 7x) + (4y – 3y) + (7 – 1)

= (2 – 7)x + (4 – 3)y + 6

= 5x + y + 6

6. Anima, Mamoni, Rita and Purabi’s marks of their mathematics examination are as follows –

Mamoni has obtained double the marks of more than Anima.

Rita has got four marks less than Anima

Purabi has got two marks more than Mamoni

Now find out the sum of their marks in algebraic expression.

Ans: Let Anima gets marks in Mathematics = x

∴ Mamoni gets 2x

Rita gets (x – 4)

And Purabi gets 2x + 2

∴ The sum of their marks in algebraic expression”

x + 2x + (x – 4) + (2x + 2)

= 6x – 2

7. Subtract 2x² + y² + 7x + 3 from the sum of 3x² + 2x + 1 and y² – 4x – 2

Ans: [(3x² + 2x + 1) + (y² – 4x – 2)] – (2x² + y² + 7x + 3)

= [3x² + 2x + 1 + y² – 4x – 2] – (2x² + y² + 7x + 3)

= [3x² + (2x – 4x) + y² + (1 – 2)] – (2x² + y² + 7x + 3)

= (3x² – 2x + y² – 1) – (2x² + y² + 7x + 3)

= 3x² – 2x + y² – 1 – 2x² – y² – 7x – 3

= (3x² – 2x²) + (2x – 7x) + (-1 – 3)

= (3 – 2)x² + (-2 – 7)x + (-4)

= x² + (-9)x – 4

= x² – 9x – 4

8. Subtract the sum of 2x² – x and x² + 6x + 2 from the sum of 2x² + 7x and 3x – 7

Ans: [(2x² + 7x) + (3x – 7)] – [(2x² – x) + (x² + 6x + 2)]

= [2x² + 7x + 3x – 7] – [2x² – x + x² + 6x + 2]

= (2x² + 10x – 7) – (3x² + 5x + 2)

= 2x² + 10x – 7 – 3x² – 5x – 2

= (2x² – 3x²) + (10x – 5x) – 7 – 2

= (2 – 2)x² + (10 – 5)x + (-9)

= -x² + 5x – 9

9. The measure of the boundary of a paddy field is x, and x/2,y y/2 respectively. What is the perimeter of the land?

Ans: The measurements of the four boundaries of the plot are x, x/2,y and y/2 respectively

∴ Perimeter of the land = x + x/2 + y + y/2

= (1 + 1/2)x + (1+ 1/2)y

= 3/2x + 3/2y

= 3/2(x + y)

10. Nabin has some marbles. Bijay has 4 marbles less than the square of the numbers of marbles with Nabin, Anup has 4 more marbles than the marbles with Bijay, Prakash has said that he has 6 more marbles than the sum of the marbles with Nabin, Bijay and Anup. Express the total number of the marbles with Nabin, Bijay, Anup and Prakash in algebraic expression.

Ans: Let the number of marbles with Nabin = x, marbles with Bijay = (x² – 4), marbles with Anup = {(x² – 4) + 4} and marbles with Prakash

= x + x² – 4 + (x² – 4) + 4 + 6

∴ The total number of marbles

= x + x² – 4 + (x² – 4 + 4) + x + x² – 4 + (x² – 4) + 4 + 6

= x + x² – 4 + x² – 4 + 4 + x + x² – 4 + x² – 4 + 4 + 6

= 4x² + 2x – 8 + 6

= 4x² + 2x – 2

Exercise 12.3

1. Find the value of the following algebraic expressions, if a = 1

(i) 2a + 1

Ans: 2a + 1

= 2 × 1 + 1

= 2 + 1

= 3

(ii) a² – 2a + 1

Ans: a² – 2a + 1

= 1² – 2 × 1 + 1

= 1 – 2 + 1

= 2 – 5

= 0

(iii) a + 3/4

Ans: a + 3/4

= 1 + 3/4

= 4/4

= 1

(iv) 1/2a – 4

Ans: 1/2a – 4

= 1/2 × 1 – 4

= 1/2 – 4

= 1 – 8/2

= -7/2

(v) a³ + a² + a – 1

Ans: a³ + a² + a – 1

= 1³ + 1² + 1 – 1

= 1 + 1 + 1 – 1

= 3 – 1

= 2

2. If x = – 3 then find the value of the following algebra expressions.

(i) -x² + 4x + 3

Ans: -x² + 4x + 3

= -(-3)² + 4(-3) + 3

= -9 – 12 + 3

= -21 + 3

= -18

(ii) 2x² + x + 3

Ans: 2x² + x + 3

= 2(-3)² + (-3) + 3

= 2 × 9 – 3 + 3

= 18

(iii) x³ – x² + 1

Ans: x³ – x² + 1

= (-3)³ – (-3)² + 1

= -27 – 9 + 1

= -36 + 1

= -35

(iv) 3x + 1

Ans: 3x + 1

= 3(-3) + 1

= -9 + 1

= -8

(v) x/3 + 2/3

Ans: x/3 + 2/3

= -3/3 + 2/3

= (-3 + 2)/3

= -1/3

3. Find the value of the algebraic expressions when x = 1 and y = – 1

(i) x² + xy + y²

Ans: x² + xy + y²

= 1² + 1 × (-1) + (-1)²

= 1 – 1 + 1

= 1

(ii) x² + y²

Ans: x² + y²

= 1² + (-1)²

= 1 + 1

= 2

(iii) x² – y²

Ans: x² – y²

= (1)² – (-1)²

= 1 – 1

= 0

(iv) x² + y + 1

Ans: x² + y + 1

= 1² + (-1) + 1

= 1 – 1 + 1

= 1

(v) 3x + y

Ans: 3x + y

= 3 × 1 + 1(-1)

= 3 – 1

= 2

(vi) x²y + xy² + x

Ans: x²y + xy² + x

= 1²(-1) + 1 × (-1)² + 1

= 1(-1) + 1 × 1 + 1

= -1 + 1 + 1

= 1

4. Simplify the following expression and find values for x = – 2

(i) x² + x + 7 + x + x² – 1

Ans: x² + x + 7 + x + x² – 1

= 2x² + 2x + 6

= 2(-2)² + 2 (-2) + 6

= 8 – 4 + 6

= 8 + 6 -4

= 14 – 4

= 10

(ii) 3(x + 4) + 2x + 1

Ans: 3(x + 4) + 2x + 1

= 3(-2 + 4) + 2(-2) + 1

= 3 × 2 – 4 + 1

= 6 – 4 + 1

= 7 – 4

= 3

(iii) 3x – (2x – 1)

Ans: 3x – (2x – 1)

= 3(-2) – [2(-2) – 1]

= -6 – 4 – 1

= -6 – (-5)

= -6 + 5

= -1

(iv) (x² + x) – (2x² – x + 1)

Ans: (x² + x) – (2x² – x + 1)

= [(-2)² + (-2)] – [2(-2)² – 2) + 1

= [4 – 2] – [2 × 4 + 2 + 1]

= 2 – (8 + 2 + 1)

= 2 – 11

= -9

(v) x³ + 2x² – x + 2x² + 2x + 1

Ans: x³ + 2x² – x + 2x² + 2x + 1

= (-2)³ + 2(-2)² – 2 + 2(-2)² + 2(-2) + 1

= 8 + 2 × 4 + 2 + 2 × 4 – 4 + 1

= -8 + 8 + 2 + 8 – 4 + 1

= 7

(vi) x³ – 4(x – 5)

Ans: x³ – 4(x – 5)

= (-2)³ 4(-2 – 5)

= -8 – 4(-7)

= -8 + 28

= 20

5. Simplify the expression given below and find the value for x = 2, y = – 3 and z = – 1.

(i) 2x + y – z + 3x – 2y + z

Ans: Given that, x = 2, y = -3, z = -1

2x + y – z + 3x – 2y + z

= 2 × 2 + (-3) – 1 + 3 × 2 – 2(-3) + (-1)

(ii) xy + yz + 2x

Ans: xy + yz + 2x

= 2(-3) + (-3)(-1) + 2 × 2

= -6 + 3 + 4

= 1

(iii) 2x²y + xy²z + 3xyz + 6x²y – 2xy²z – 6xyz

Ans: 2x²y + xy²z + 3xyz + 6x²y – 2xy²z – 6xyz

= 2 × 2² × (-3) + 2 × (-3)² × (-1) + 3 × 2 × (-3) × (-1) + 6 × 2² × (-3) – 2 × 2 × (-3)² × (-1) – 6 × 2 × (-3) × (-1)

= 2 × 4 × (-3) + 2 × 9 × (-1) + 6 × (-3) × (-1) + 6 × 4 × (-3) – 4 × 9 × (-1) – 6 × 2 × (-3) × (-1)

= -24 – 18 + 18 – 72 + 36 – 36 = -96

(iv) 5 – 3x + 2y – 7x + 6y + 2 + z

Ans: 5 – 3x + 2y – 7x + 6y + 2 + z

= 5 – 3 × 2 + 2 × (-3) – 7 × 2 + 6 × (-3) + 2(-1)

= 5 – 6 – 6 – 14 – 18 + 2

= 7 – 45 = -38

(v) (2x + y + z) – (z – 3y) + (2 + x) – (5 – z)

Ans: (2x + y + z) – (z – 3y) + (2 + x) – (5 – z)

= {2 × 2 + (-3) + (-1)} + {(-1) -3(-3)} + (2 + 2) + {5 – (-1)}

= {4 – 3 – 1} + {-1 – 9} + 4 + (5 + 1)

= 0 + (-10) + 4 + 6

= -10 + 10 = 0

6. For x = 0 if the value of the expression x² + 2x – p + 1 is 6 then find the value of p.

Ans: x² + 2x – p + 1 = 6

⇒ 0² + 2 × 0 – p + 1 = 6

⇒ -p + 1 = 6

⇒ -p = 6 – 1

⇒ -p = 5

⇒ p = -5

Exercise 12.4

1. Fill the table with the values of the following algebraic expressions [use 1, 2, 3,…….. in place of the unknown variables]

	Expression	Terms
		1st	2nd	3rd	4th	5th	50th	……	100th
(i)	5n + 1	6	11
(ii)	3n – 1	2		8
(iii)	x² + 1	2			17
(iv)	2x + 3	5		9		13			203
(v)	4n – 1	3					199

Ans:

	Expression	Terms
		1st	2nd	3rd	4th	5th	50th	……	100th
(i)	5n + 1	6	11	16	21	26	251		501
(ii)	3n – 1	2	5	8	11	14	149		299
(iii)	x² + 1	2	5	10	17	26	2501		1001
(iv)	2x + 3	5	7	9	11	13	103		204
(v)	4n – 1	3	7	11	15	19	199		399

2. Observe the following diagram:

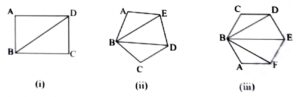
In the quadrilateral AmBCD only one diagonal can be drawn from the vertex B. (Fig.i)

In the pentagon ABCDE only 2 diagonals can be drawn from one vertex B. (Fig. ii)

In the hexagon ABCDEF only 3 diagonals can be drawn from the vertex B. (Fig. iii)

∴ number of diagonal can be drawn from a vertex of a quadrilateral = 1

number of diagonal can be drawn from a vertex of a pentagon = 2

number of diagonal can be drawn from a vertex of a hexagon = 3

How many diagonals can be drawn from a vertex of a heptagon?

How many diagonals can be drawn from a vertex of a polygon of side n’ ?

Ans: No. of diagonals can be drawn from a vertex of a heptagon = 4.

[No. of diagonals can be drawn from the vertex of n-sided polygon = (n-3)

3. In the table given below one value of ‘n’ is given for n = 1, 2, 3, 4, 5 and some has to find. Fill up the gaps.

(a)

n	1	2	3	4	5
term	1	4	9	16	?

What is the nth term = ?

Ans:

n	1	2	3	4	5
term	1	4	9	16	25

nth term = n²

(b)

n	1	2	3	4	5	–	n
term	4	7	10	13	?		?

Ans:

n	1	2	3	4	5	–	n
term	4	7	10	13	16		3n + 1

nth term = 3n + 1

(c)

n	1	2	3	4	5	6
term	8	10	12	14	16	?

What is the nth term = ?

Ans:

n	1	2	3	4	5	6
term	8	10	12	14	16	18

nth term = 2n + 6

FAQs