SEBA Class 7 Maths Chapter 13 Exponents and Powers Solutions | SCERT Assam
Find SEBA Class 7 Maths Chapter 13 Exponents and Powers Solutions for Exercises 13.1, 13.2, and 13.3 in English Medium, as per the SCERT Assam syllabus. This chapter explains laws of exponents, standard form of numbers, and their applications. Our step-by-step solutions help students understand how to simplify and calculate expressions using exponents and powers.Scan QR Code: N3K6E7
📚 Get Complete SEBA Class 7 Maths Solutions – Access step-by-step solutions for all chapters as per the SCERT Assam syllabus.
➡ Click here for full subject solutions
Exponents and Powers
Exercise – 13.1 |
|---|
Q. 1. Find out the correct answer.
(i) The value of (-1)⁵ is
(a) -1
(b) 1
(c) 5
(d) -5
Ans: (a) -1
(ii) The value of (-5)⁴ is
(a) -625
(b) 625
(c) 256
(d) -256
Ans: (b) 625
2. Express in exponential form
(i) 5 × 5 × 5 × 5 × 5
Ans: 5 × 5 × 5 × 5 × 5 = 5⁵
(ii) 3 × 3 × 2 × 2 × 2
Ans: 3 × 3 × 2 × 2 × 2 = 3² × 2³
(iii) (-2) × (-2) × (-2) × 3 × 3 × 3 × 3
Ans: (-2) × (-2) × (-2) × 3 × 3 × 3 × 3 = (-2)³ × 3⁴
(iv) b × b × b × b × b × c × c × c
Ans: b × b × b × b × b × c × c × c = b⁵ × c³
(v) a × a × a × b × b × c × c × c × c × c
Ans: a × a × a × b × b × c × c × c × c × c = a³ × b² × c⁵
3. Find the value of-
(i) 2⁷
Ans: 2⁷ = 2 × 2 × 2 × 2 × 2 × 2 × 2
= 128
(ii) (-2)⁷
Ans: (-2)⁷ = (-2) × (-2) × (-2) × (-2) × (-2) × (-2) × (-2)
= -128
(iii) 3⁶
Ans: 3⁶ = 3 × 3 × 3 × 3 × 3 × 3
= 729
(iv) (-3)⁶
Ans: (-3)⁶ = (-3) × (-3) × (-3) × (-3) × (-3) × (-3)
= -729
(v) 2⁵ × 4⁴
Ans: 2⁵ × 4⁴ = 2 × 2 × 2 × 2 × 2 × 4 × 4 × 4 × 4
= 32 × 256
= 8192
(vi) 5² × 3³
Ans: 5² × 3³ = 5 × 5 × 3 × 3 × 3 = 25 × 27
= 675
(vii) (-3)² × (-5)³
Ans: (-3)² × (-5)³ = (-3)² × (-5)³
= 9 × (-125)
= -1125
4. Express in exponential form:
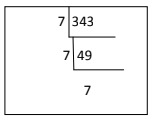
(i) 343
Ans: 343
= 7 × 7 × 7
= 73
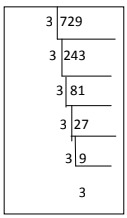
(ii) 729
Ans: 729
= 3 × 3 × 3 × 3 × 3 × 3
= 36
(iii) 2187
Ans: 2187
= 3 × 3 × 3 × 3 × 3 × 3 × 3
= 3⁷
(iv) -2187
Ans: -2187
= (-3) × (-3) × (-3) × (-3) × (-3) × (-3) × (-3)
= (-3)⁷
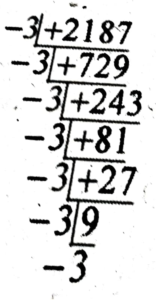
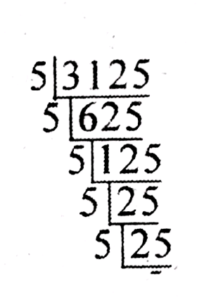
(v) 3125
Ans: 3125
= 5 × 5 × 5 × 5 × 5
= 5⁵
(vi) -3125
Ans: -3125
= (-5) × (-5) × (-5) × (-5) × (-5)
= (-5)⁵
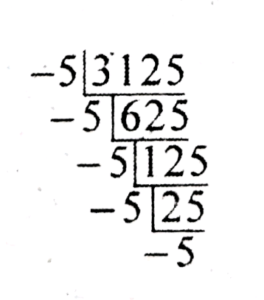
5. Express each of the following numbers as product of the powers of their prime factors:
(i) 100
Ans: 100 = 2² × 5²
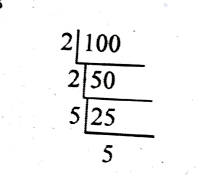
(ii) 300
Ans: 300 = 2² × 3 × 5²
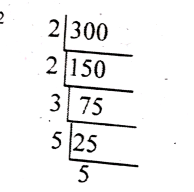
(iii) 1000
Ans: 1000 = 2³ × 5³

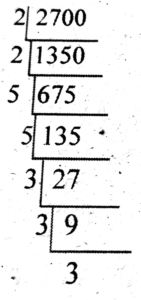
(iv) 2700
Ans: 2700 = 2² × 5² × 3³
(v) 405
Ans: 405 = 5 × 3⁴
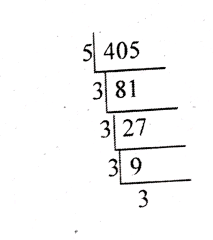
(vi) 1600
Ans: 1600 = 2⁶ × 5²

6. Fill in the blanks with appropriate sign (>, < or =).
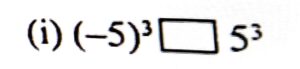
Ans: (- 5)³ < 5³
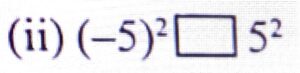
Ans: (-5)² = 5²
![]()
Ans: (-7)⁴ = 7⁴

Ans: (-1)¹⁵ < (-1)¹⁰
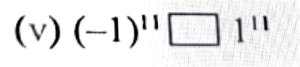
Ans: (-1)¹¹ < (-1)¹¹
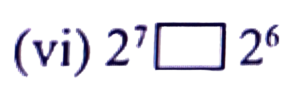
Ans: 2⁷ > 2⁶
7. If 2592 = 2ᵐ × 3ⁿ, then find the value of m and n.
Ans: 2592 = 2ᵐ × 3ⁿ
⇒ 2⁵ × 3⁴ = 2ᵐ = 3ⁿ
∴ m = 5 and n = 4
8. If 16875 = 3ᵐ × 5ⁿ, then find the value of m and n.
Ans: 16875 = 3ᵐ × 5ⁿ
⇒ 3³ × 5⁴ = 3ᵐ × 5ⁿ
∴ m = 3 and n = 4
Exercise 13.2 |
|---|
1. Simplify using laws of exponents (Write the answer in the exponential form)
(i) 3⁵ × 3⁷ × 3¹⁰
Ans: 3⁵ × 3⁷ × 3¹⁰ = 3⁵⁺⁷⁺¹⁰
= 3³²
(ii) (2⁷ × 2⁶) ÷ 2⁵
Ans: (2⁷ × 2⁶) ÷ 2⁵
= 2⁷⁺⁶ ÷ 2⁵ = 2¹³ ÷ 2⁵
= 2¹³⁻⁵
= 2⁸
(iii) (2⁰ × 2⁵ × 2⁸) ÷ (2⁰ × 2⁶ × 2⁷)
Ans: (2⁰ × 2⁵ × 2⁸) ÷ (2⁰ × 2⁶ × 2⁷)
= (1 × 2⁵⁺⁸) ÷ (1 × 2⁶⁺⁷)
= 2¹³ ÷ 2¹³
= 2¹³⁻¹³
= 2⁰ = 1
(iv) (3⁴)² × (3²)³
Ans: (3⁴)² × (3²)³
= 3⁸ × 3⁶
= 3⁸⁺⁶
= 3¹⁴
(v) (16² × 8³) ÷ (2⁵)²
Ans: (16² × 8³) ÷ (2⁵)²
= {(24)7 × (23)3} ÷ (210)
= (228 × 29) ÷ 210
= 228+9 ÷ 210
= 237 ÷ 210
= 237-10
= 227
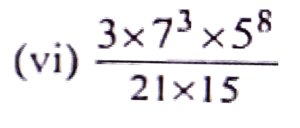
Ans:
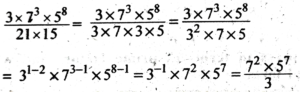

Ans:
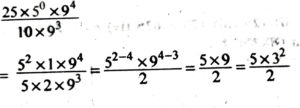
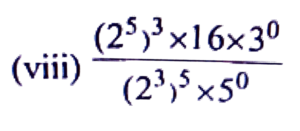
Ans:
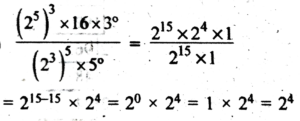
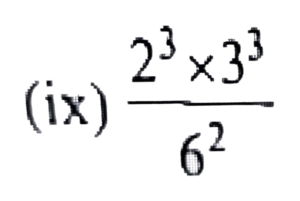
Ans:
![]()
![]()
Ans:
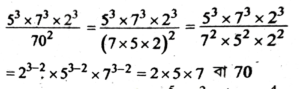
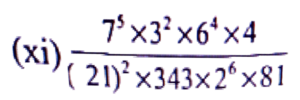
Ans:
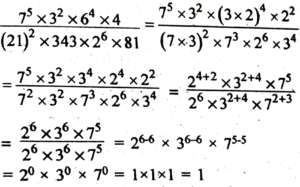
2. Express in terms of prime factors and write in exponential form-
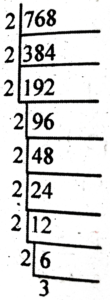
(i) 768
Ans: 768
= 2⁸ × 3
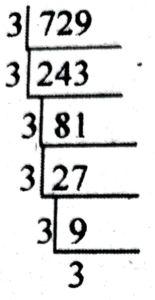
(ii) 729
Ans: 729 = 3 × 3 × 3 × 3 × 3 × 3
= 3⁶
(iii) 128 × 625
Ans: 128 × 625
= 2⁷ × 5⁴

(iv) 64 × 729
Ans: 64 × 729
= 2⁶ × 3⁶

(v) 1000
Ans: 1000
= 23 × 53
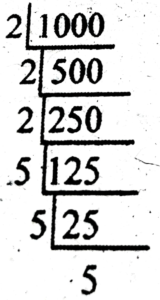
3. Simplify:
![]()
Ans:
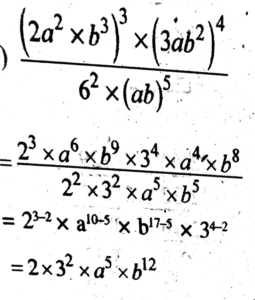
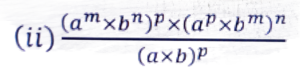
Ans:
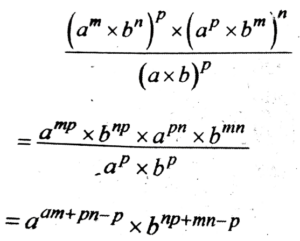
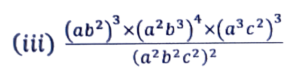
Ans:
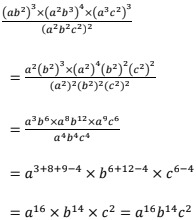
4. If 3m = 81, then find the value of m.
Ans: 3ᵐ = 81
⇒ 3ᵐ = 3⁴
∵ m = 4
5. Check whether it is true or false.
(i) 3a⁰ = (3a)⁰
Ans: Incorrect.
(ii) 2³ > 3²
Ans: Incorrect.
(iii) (5⁰)⁴ = (5⁴)⁰
Ans: Correct.
(iv) 2³ × 3³ = 6⁵
Ans: Incorrect.
(v) 2⁵/3⁵ = (2/3)⁵⁻⁵
Ans: Incorrect.
(vi) 2⁵ = 5²
Ans: Incorrect.
Exercise 13.3 |
|---|
1. Express one following numbers in standard form:
(i) 5,273,294
Ans: 5273294 = 5.273294 × 10⁶
(ⅱ) 7,10,021
Ans: 710021 = 7.10021 × 10⁵
(iii) 6,400,000
Ans: 6400000 = 6.4 × 106
(iv) 18,129
Ans: 18129 = 1.8129 × 10⁴
(v) 23961,32
Ans: 2396132 = 2.396132 × 10⁶
(vi) 75,000,000,000
Ans: 75000000000 = 7.5 × 10¹⁰
(vii) 70,010,000,000
Ans: 70010000000 = 7.001 × 10⁷
(viii) 45026.9
Ans: 45026.9 = 4.50269 × 10⁴
(ix) 3206.19
Ans: 3206.19 = 3.20619 × 10³
(x) 475000000000
Ans: 475000000000 = 4.75 × 1011
2. Express the numbers in following statement in standard form-
(i) Radius of Moon 1737.1 km.
Ans: 1 .7371 × 103 km.
(ii) Radius of Earth 6771000 m.
Ans: 6.7771 × 106 m.
(iii) Distance between Mercury and Venus 50,290,000 km.
Ans: 5.029 × 107 km.
(iv) Distance between Mercury and Jupiter 720,420,000 km.
Ans: 7.2042 × 10⁸
(v) 1 light year = 9,460,700,000,000 km.
Ans: 9.4607 x 10¹²
(vi) 1 Nautical Unit (AU) = 149,600,000 km.
Ans: 1.496 × 10⁸ km.
(vii) Mass of Moon 73490,000,000,000,000,000,000 km.
Ans: 7.349 × 10²² kg.
(viii) Radius of the Sun 695510 km.
Ans: 6.9551 × 10⁵ km.
(ix) There is 1,386,000,000 cubic Kilometer sea water on Earth.
Ans: 1.386 × 10⁹ cu. km
(x) Speed of light in Vacuum 299,792,458 meter/second (approx 3000,000,000 meter/second).
Ans: 2.99792458 × 108 m/sec.
3. Compare (which one is greater)
(i) 57610000000000000; 576000000000000000
Ans: 57610000000000000
= 5.761 × 106 > 5.76 × 1017
(ii) 343.6 × 10¹⁹; .03436 × 10¹⁷
Ans: 343.6 × 1010 > 0.03436 × 10¹⁷
