SEBA Class 7 Maths Chapter 5 Lines and Angles Solutions | SCERT Assam | Assam English Medium | Exercises 5.1, 5.2 & 5.3

Get SEBA Class 7 Maths Chapter 5 Lines and Angles Solutions for Exercises 5.1, 5.2, and 5.3 in English Medium, following the SCERT Assam syllabus. Understand key concepts like types of angles, intersecting lines, parallel lines, and angle properties with step-by-step solutions. Ideal for SEBA students seeking clear and accurate explanations. QR Code: B4V9B5.

📚 Get Complete SEBA Class 7 Maths Solutions – Access step-by-step solutions for all chapters as per the SCERT Assam syllabus.

➡ Click here for full subject solutions

Lines and Angles

Exercise – 5.1

1. Find out the complementary angles of the following:

(a) 45°

Ans: The complementary angle of (90° – 45°) = 45°

(b) 65°

Ans: The complementary angle of (90° – 65°) = 25°

(c) 41°

Ans: The complementary angle of (90° – 41°) = 49°

(d) 54°

Ans: The complementary angle of (90°- 45°) = 36°

2. If the difference of measures of a pair of complementary angles is 22 ° Find the angles.

Ans: Let the measure of a pair of complementary angles are x° and 90° – x

∴ A/Q, x – (90° – x) = 22°

⇒ x – 90° + x = 22°

⇒ 2x = 22° + 90°

⇒ 2x = 112°

⇒ x = 112°/2 = 56°

∴ measure of two complementary angles are 56° and (90° – 56°) = 34°

3. Write down the measures of the angles supplementary to each of the following angle.

(a) 100°

Ans: 180° – 100° = 80°

(b) 90°

Ans: 180° – 125° = 55°

(c) 55°

Ans: 180° – 55° = 125°

(d) 125°

Ans: 180° – 125° = 55°

4. A pair of supplementary angles is such that the larger angle is 44° more than the smaller angle. Find the measures of the angles.

Ans: Let the larger angle of a pair of supplementary angles x° and the smaller angle = 180 ° – x°

∴ A/Q, x° = 180° – x° + 44°

⇒ 2x° = 224°

⇒ x° = (224°)/2

⇒ x° = 112°

∴ Larger angle = 112° and smaller angle = 180° – 112° = 68°

5. The lines PQ and RS intersect at O. If angle POR = 50° then find the measures of the other angles.

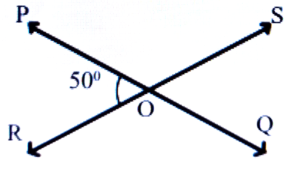
Ans: ∠POR = 50°

∴ ∠SOQ = 50°

∠POR = ∠POS = 180°

⇒ 50° + ∠POS = 180°

⇒ ∠POS = 180°- 50° = 130°

∴ ∠ROQ = 130°

6. Find x from the following figure.

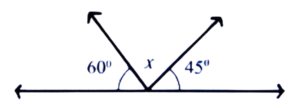
Ans: 60° + x + 45° = 180° (straight angle)

⇒ 105° + x = 180°

⇒ x = 180° – 105° = 75°

7. Find an angle which is equal to its supplementary angle.

Ans: Let the two angles be x and x

∴ x + x = 180°

⇒ 2x = 180°

⇒ x = (180°)/2

⇒ x = 90°

8. The measure of an angle is 24°more then its complementary angle. Find the measure of the angle.

Ans: Let the two complementary angles be x and x

∴ x + x + 24° = 90°

⇒ 2x = 90° – 24°

⇒ 2x = 66°

⇒ x = (66°)/2

= 33°

∴ Two angles are 33° and 33° + 24° = 57°

9. The measure of an angle is 32° less then its complementary angle. Find the measure of the angle

Ans: Let the two complementary angles are x and x – 32° x + x – 32° = 90°

⇒ 2x = 90° + 32°

⇒ 2x = 122°

⇒ x = (122°)/2 = 61°

∴ Measure of the angles are 61° and (61 ° – 32°) = 29°

10. The measure of an angle is five times the measure of its complementary angle. Find the measure of the angle.

Ans: Let the two complementary angles are x and 5x.

∴ x + 5x = 90°

⇒ 6x = 90°

⇒ x = (90°)/6

⇒ x = 15°

∴ The measure of the angle = 5 × 15° = 75°

11. An angle is five times the measure of its more than its supplementary angle. Find the measure of the angle.

Ans: Let the two angles are x and 5x. x + 5x = 180°

⇒ 6x = 180°

⇒ x = (180°)/6

= 30°

∴ The measure of the angle

= 5 × 30° = 150°

12. The ratio of two supplementary angles is 3: 2. Find the angles.

Ans: Let the two supplementary angles are 3x & 2x.

∴ 3x + 2x = 180

⇒ 5x = 180

⇒ x = 36

∴ measure of angles are = 3 × 36° = 180° and 2 × 36° = 72°

13. The ratio of two complementary angles is 4: 5.Find the angles.

Ans: Let the two angles are 4x and 5x

∴ 4x + 5x = 90°

⇒ 9x = 90 °

⇒ x = (90°)/9 = 10°

∴ Two angles are 4 × 10° = 40° and 5 × 10° = 50°

14. Find x and y from the following diagrams.

(a)

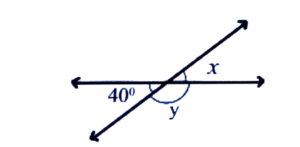
Ans: x = 40° [Vertically opp. angels]

x + y = 180°

⇒ 40 + y = 180

⇒ y = 180 – 40 = 140

(b)

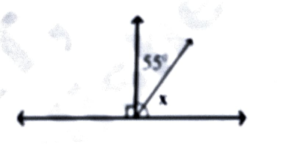
Ans: x = 90° – 55° = 35°

⇒ x = 90° – 55° = 35°

15. Identify the pairs of complementary angles from the following.

(a) 65°, 25°

(b) 63°, 27°

(c) 112°, 68°

(d) 130°, 50°

Ans: (a) 65°, 25° and

(b) 63°, 27°

16. Identify the pairs of supplementary angles from the following.

(a) 110°, 70°

(b) 163°, 270

(c) 112°, 68°

(d) 45°, 45°

Ans (a) 110°, 70° and

(c) 112°, 68°

Exercise – 5.2

1. In the following figure if AB || CD, find x, y and z.

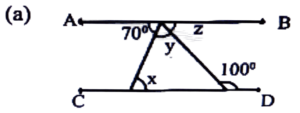
Ans: ∠x = 70° (Alternate angle)

∠y = 180° – (70° + 80°) = 180° – 150° = 30°

∴ ∠z = 180° – (70° + 30°) = 180° – 100° = 80°

x = 70°

y = 30°

z = 80°

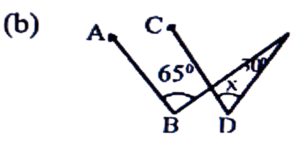
Ans: x = 30° + 180° – 65° = 180°

⇒ x = 65° – 30°

= 35°

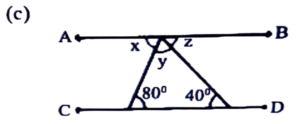
Ans: x = 80° (Alternate angle)

z = 40°

∴ y = 180° – (80° – 40°)

= 180° – 120°

= 60°

(d)

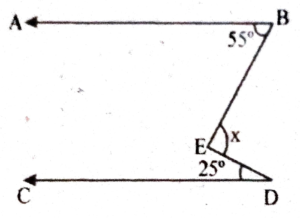
Ans: ∠BFD = 55°

∠BFD = 180° – (55° + 250°)

= 180°- 80° = 100°

∴ x = 180° – 100°

= 80°

2. In the following figures, I and m are two lines and n is a transversal. Find the pair of lines which are parallel to each other?

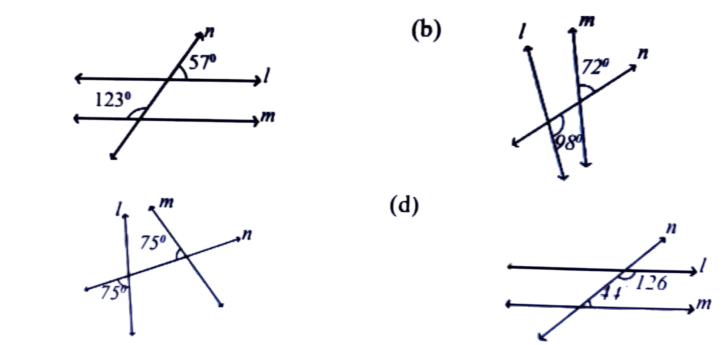
Ans: (a) and (d)

3. From the figure find given below the measure of x.

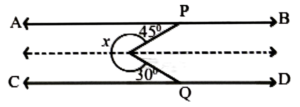
Ans: x = 360° – (45° + 30°)

= 360° – 57° = 285°

4. In the figure given below 1 || m, t is transversal. Find the value of x.

Ans: x = 120°

Ans: x = 180° – 60° = 120° x = 60°

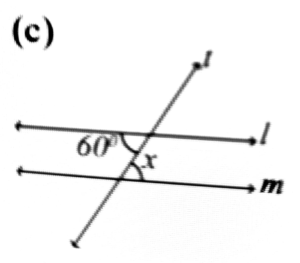
Ans: 60° + x = 180°

x = 180° – 60° x = 120°

Exercise – 5.3

1. If a pair of adjacent angles are supplementary to each other, then they will form-

(a) corresponding angles.

(b) vertically opposite angles.

(c) linear pair of angles.

(d) a ray.

Ans. (c) linear pair of angles.

Q.2. If two angles are supplementary their sum will be-

(a) 90°

(b) 180°

(c) 360°

(d) 45°

Ans. (b) 180°

Q.3. If two angles are complementary to each other, their sum will be-

(a) 45°

(b) 180°

(c) 90°

(d) 360°

Ans. (c) 90°

4. In the adjoining figure if l ||m then ∠1 = ∠2 since they are-

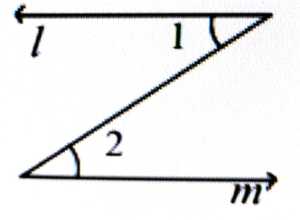
(a) corresponding angles.

(b) vertically opposite angles.

(c) alternate interior angles.

(d) supplementary angles.

Ans: (c) alternate interior angles.

5. In the figure the pair of alternate interior angles will be.

(a) ∠1, ∠3

(b) ∠2, ∠3

(c) ∠2, ∠5

(d) ∠2, ∠4

Ans: (b) ∠2, ∠3

6. If a ||b and c is a transversal, then angle y is-

(a) 90°

(b) 125°

(c) 55°

(d) 180°

Ans: (c) 55°

7. If a || b and c is a transversal, then Zy is-

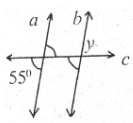
(a) 90°

(b) 25°

(c) 55°

(d) 35°

Ans: (c) 55°

8. The measure of the complementary angle of 45° is-

(a) 135°

(b) 25°

(c) 35°

(d) 45°

Ans: (d) 45°

9. Which of the following angles will be equal to its own complementary angle?

(a) 30°

(b) 25°

(c) 35°

(d) 45°

Ans: (d) 45°

10. Which of the following angles will be equal to its own supplementary angle?

(a) 60°

(b) 90°

(c) 180°

(d) Non of the above.

Ans: (b) 90°

11. If 1 || m and c is the transversal then x is-

(a) 30°

(b) 60°

(c) 90°

(d) 180°

Ans: (b) 60°

12. In the given figure 1 || m and c is transversal. The value of x is-

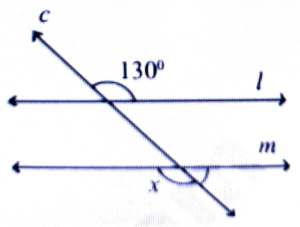
(a) 50°

(b) 130°

(c) 120°

(d) 100°

Ans: (b) 130°

13. In the given figure 1 || m and c is transversal. The value of x is-

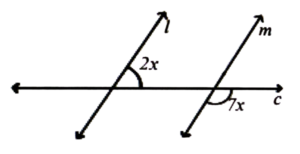
(a) 10°

(b) 200°

(c) 300°

(d) 250°

Ans: (b) 200°

14. If two lines are equidistant from each other then they are-

(a) perpendicular lines.

(b) non parallel lines.

(c) Intersecting lines.

(d) parallel lines.

Ans. (d) parallel lines.