SEBA Class 7 Maths Chapter 6 Triangle and Its Properties Solutions | SCERT Assam | Exercises 6.1 to 6.5
Find SEBA Class 7 Maths Chapter 6 Triangle and Its Properties Solutions for Exercises 6.1, 6.2, 6.3, 6.4, and 6.5 in English Medium, following the SCERT Assam syllabus. Learn about different types of triangles, triangle inequalities, Pythagoras theorem, and more with step-by-step solutions. Ideal for SEBA students looking for accurate and easy-to-understand explanations. QR Code: I8B7Y2.
📚 Get Complete SEBA Class 7 Maths Solutions – Access step-by-step solutions for all chapters as per the SCERT Assam syllabus.
➡ Click here for full subject solutions
triangle and its properties
Exercise – 6.1 |
|---|
1. How many medians are there in a triangle?
Ans: Three medians are there in a triangle.
2. How many altitudes are there in a triangle?
Ans: Three altitudes are there in a triangle.
3. Draw a triangle and display its medians.
Ans: AD. BE and CF are three medians in a triangle.
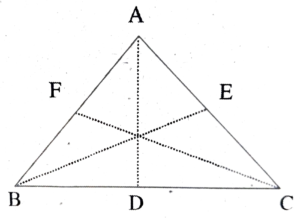
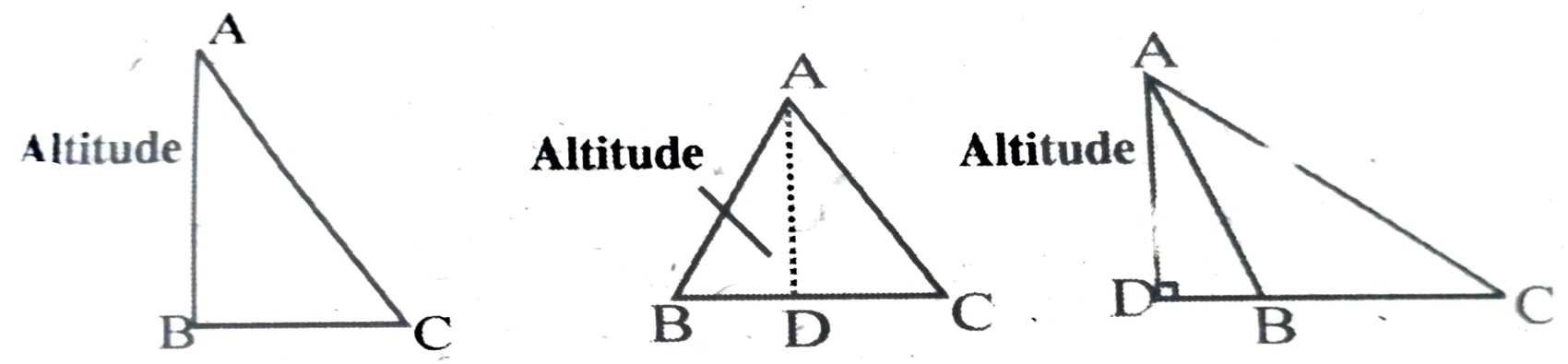
4. Draw a triangle and display its altitudes.
Ans:
5. Name the angle opposite to side LM in ΔLMN.
Ans: The angle opposite to side LM in Δ LMN is ∠LNM.
6. Name the side opposite to vertex Q of Δ PQR.
Ans: The side opposite to vertex Q of ΔPQR is PR.
7. Name the vertex opposite to side RT of ΔRST.
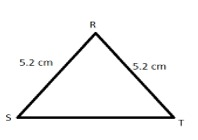
Ans: The vertex opposite to side RT of ΔRST is S.
8. (i) Tick (√) the correct answer.
In ∆PQR, PM is-
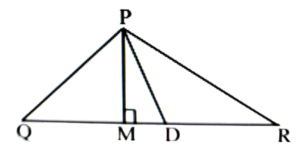
(a) A median
(b) An altitude
(c) A bisector of QR
(d) A side
Ans: (b) An altitude.
(ii) If D is the midpoint of side QR of ∆PQR, then PD is-

(a) perpendicular bisector on QR.
(b) altitude.
(c) median.
(d) opposite side of QR.
Ans: (c) Median.
Exercise – 6.2 |
|---|
1. Fill in the blanks:
(a) The angles in the interior of a triangle are called _____________.
Ans: Interior angles.
(b) The angles exterior to a triangle are called.
Ans: Exterior angles.
2. Find the value of x from the diagrams given below:

Ans: ∠x = 50° + 70° = 120°
(b)
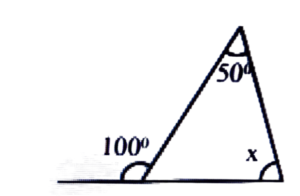
Ans: x + 50° = 100°
⇒ x = 100° – 50° = 50°
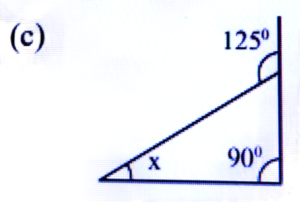
Ans: x + 90° = 125°
⇒ x = 125° – 90° = 35°

Ans: x + 30° = 120°
⇒ x = 120° – 30° = 90°
(e)
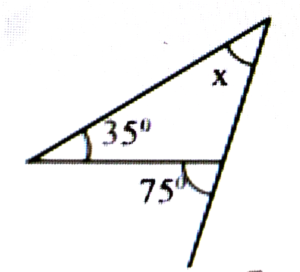
Ans: x + 35° = 75°
⇒ x = 75° – 35° = 40°
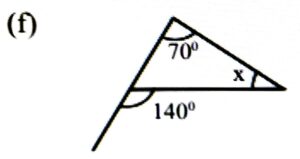
Ans: x + 70° = 140°
⇒ x = 140° – 70° = 70°
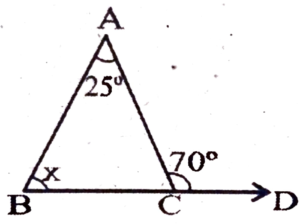
3. In a triangle, an exterior angles is 70° and one of its interior opposite angles is 25 deg. Find the value of the other interior opposite angle.
Ans:
70° = x + 25°
⇒ x = 70° – 25°
= 45°
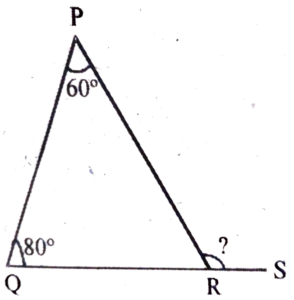
4. Two remote interior angles of a triangle are 60 deg and 80°. Find the value of the exterior angle.
Ans:
∠PRS = ∠P + ∠Q
= 60° + 80°
= 140°
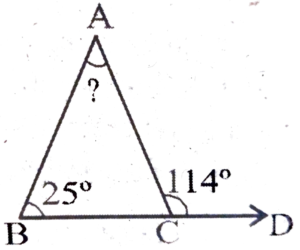
5. In a triangle, an exterior angles is 114° and one of its interior opposite angle is 25° Find the value of other distant interior angle.
Ans:
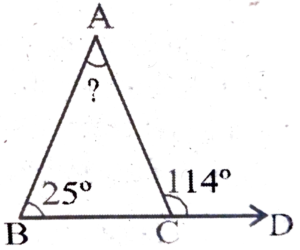
∠ACD = ∠A + ∠B
⇒ 114° = ∠A + 25°
⇒ ∠A = 114° – 25°
⇒ ∠A = 89°
6. Two remote interior angles of an exterior angle of a triangle are 49º and 41°. Find the value of the exterior angle. (Remote interior angles are also called opposite angles).
Ans:
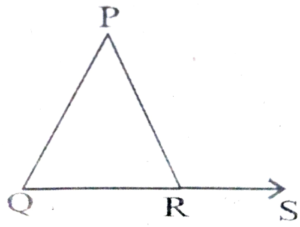
∠P + ∠Q = ∠PRS
⇒ 49° + 41° = ∠PRS
⇒ ∠PRS = 90°
Exercise – 6.3 |
|---|
1. Find the value of x from the figs given below.
Ans: x + 50° + 60° = 180°
⇒ x = 180° – 110° = 70°

Ans: x + 90° + 30° = 180°
⇒ x = 180°- 120° = 60°
Ans: ∵ Isosceles triangle
∴ ∠A = ∠C = 45°
∴ ∠A + ∠B + ∠C = 180°
⇒ 45° + x + 45° = 180°
⇒ x = 180° – 90° = 90°
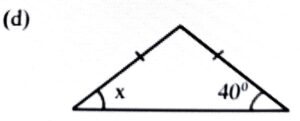
Ans: ∵ Isosceles triangle x = 40°

Ans: ∵ ∆ABC is an isosceles right angled triangle
∴ AB = CB
∠A = ∠C = 45°
⇒ x = 45°
2. Find the values of x and y from the figs given below:
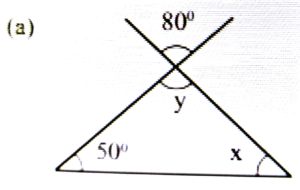
Ans: y = 80° [∴ Vertically opp. angles]
∴ x + 50° + y = 180°
⇒ x + 50° + 80° = 180°
⇒ x + 180° – 130° = 50°
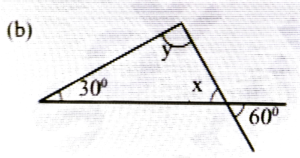
Ans: y = 60° [Vertically opp. angles]
Now, x + y + 300 = 180°
⇒ 60° + y + 30° = 180°
⇒ y = 180° – 90° = 90°
(c)

Ans: All three triangles have equal angles
∴ x + x + x = 180° [∴ x = y]
⇒ 3x = 180°
∴ x = 180°/3 = 60°
⇒ y = 60°
3. In a triangle, the measure of one angle is 60°. What will be the measure of the other two angles?
(a) 50°, 40°
Ans: 150° + 40° + 60° = 150° ≠ 180°
(b) 40°, 60°
Ans: 40° + 60° + 60° = 160° ≠ 180°
(c) 60°, 70°
Ans: 60° + 70° + 60° = 190° ≠ 180°
(d) 50°, 70°
Ans: 50° + 70° + 60° = 180°
∴ 50°, 70°
4. Find the value of ∠P from the figures given below-
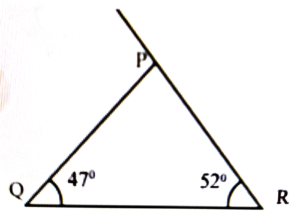
Ans: ∠P = 52° + 47° = 99°
5. Two angles of a triangle are 30° and 80°. Find the measure of the third angle.
Ans: Let the third angle is x°
∴ x° + 30° + 80° = 180°
⇒ x° = 180° – 110° = 70°
6. One angle of a triangle is 80° and the other two angles are equal. What are the measures the other tow angles?
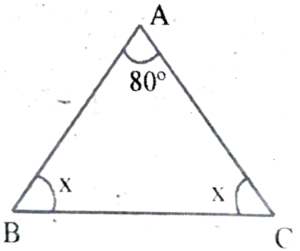
Ans: One angle of a triangle is 80° and the other two angles are equal.
(Let ∠B = ∠C = X )
∴ ∠A + ∠ B + ∠C = 180°
⇒ 80° + ∠B + ∠C = 180°
⇒ 80° + x + x = 180°
⇒ 2x = 180° – 80° = 100°
⇒ x = (100°/2) = 50°
∴ ∠B = ∠C = 50°
7. The ratio of three angles of a triangle is 1:2:1. Find the measures of the angles.
Ans: The ratio of three angles of a triangle is 1:2:1, let three angles are x, 2x and x.
∴ x + 2x + x = 180°
⇒ 4x = 180°
⇒ x = (180°)/4 = 45°
∴ The measure of the angles are 45°, 90°, 45°.
8. The angles of a triangle are (x + 21°) (x – 20°) and (2x – 45°) Find x.
Ans: Three angles of a Delta are, (x + 21°), (x – 20°) আৰু (2x – 45°)
∴ (x + 21°) + (x – 20°) + (2x – 45°) = 180°
⇒ 4x + (21°- 20°- 45°) = 180°
⇒ 4x = 180° + 44°
⇒ 4x = 224°
∴ x = 224°/4 = 56°
x = 56°
9. The ratio of three angles of a traingle is 1:2:3. Find the measures of the angles.
Ans: The ratio of three angles of a triangle is 1:2:3. Let three measures of angles are x, 2x, 3x.
∴ x + 2x + 3x = 180°
⇒ 6x = 180°
⇒ x = 180°/6 = 30°
∴ The measures of the angles are 30°, 60° and 90°.
10. In ∆ ABC, ∠A + ∠B = 116°, ∠B + ∠C = 126 ° Find out the measures of the interior angles of the triangle.
Ans: ∴ ∠A + ∠B + ∠C = 180°
⇒ 116° + ∠C = 180°
⇒ ∠C = 180° – 116 ° = 64°
∴ ∠B + ∠C = 126°
⇒ ∠B + 64° = 126°
⇒ ∠B = 126° – 64° = 62°
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 62° + 64° = 180°
⇒ ∠A + 126° = 180°
⇒ ∠A = 180° – 126° = 54°
∴ ∠A = 54°, ∠B = 62° আৰু ∠C = 64°
11. In ∆ABC, 2 ∠A = 3 ∠B = 6 ∠C. Find out ∠A, ∠B, ∠C
Ans: ∆ABC,2 ∠A = 3 ∠B = 6 ∠C
Now, 3 ∠B = 6 ∠C
⇒ ∠B = 6/3 ∠C = 2 ∠C
2∠A = 6∠C
∴ ∠A = 6/2 ∠C = 3 ∠C
Now, ∠A + ∠B + ∠C = 180°
⇒ 3 ∠C + ∠A + ∠C = 180°
⇒ 6 ∠C = 180°
⇒ ∠C = 30°
∴ ∠A = 3 × 30° = 90°
∠B = 2 × 30° = 60°
∠C = 30°
12. In the figure given below ∠CAB = 40°, AC = AB and BC = BD Find out
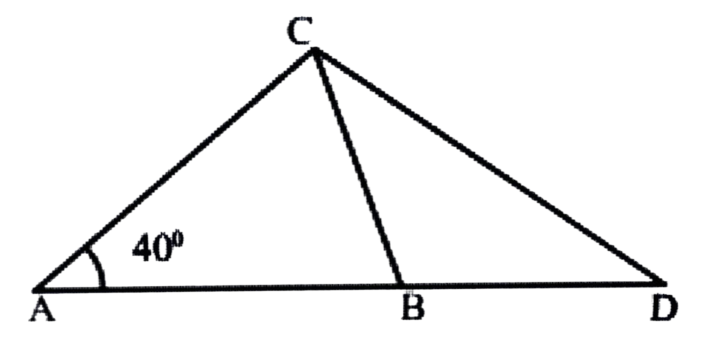
(a) ∠ACB and
(b) ∠CDB
Ans: In the figure, ∠CAB = 40°
AC = AB
∴ ∠C = ∠B
Now, ∠A + ∠B + ∠C = 180°
⇒ 40° + 2 ∠B = 180°
⇒ 2 ∠B = 180° – 40°
∴ ∠B = 140°/2 = 70°
∴ ∠C = 70°
∴ ∠CBD = 40° + 70° = 110°
That, ∠ACB = 70°
Again, BC = BD
∴ ∠BCD = ∠CDB
∴ ∆BCD get from, ∠CBD + ∠BCD + ∠CDB = 180°
⇒ ∠110° + 2 ∠CDB = 180°
⇒ 2180° CDB = 180° – 110°
⇒ ∠CDB = 70°
∴ ∠CDB = 70°/2 = 35°
∴ (a) ∠ACB = 70°, (b) ∠CDB = 35°
Exercise – 6.4 |
|---|
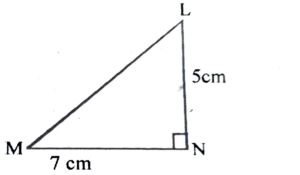
1. In the following figure AB = 10cm AC = 17cm and AD = 8cm. Determine BC.
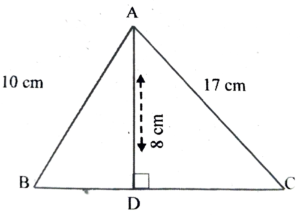
Ans: In the figure, AB = 10 cm
BC = 17 cm and AD = 8 cm
∴ BD² = AB² – AD²
= 100² – 8² = 100 – 64 = 36
![]()
∴ CD = BC – BD = (17 – 6) cm = 11 cm
∴ AC² = AD² + CD²
= 8² + 11² = 64 + 121 = 185
![]()
2. In the perimeter of a triangle is 15 cm and two sides are 5 cm and 7 cm then what is the length of the third side.
Ans: Perimeter = 15cm, two sides are 5 cm and 7 cm.
∴ Measure of third side
= 15 – (5 + 7) cm
= (15-12) cm
= 3cm.
3. In a rectangle the lengths of two adjacent sides are 16 cm and 12 cm. Find out the lengths of two diagonals.
Ans: AD = 16cm,
CD = 12cm
∴ ∆ACD-[In ∆ACD ]
AC² = AD² + CD²
⇒ AC² = 16² + 12²
⇒ AC² = 256 + 244 = 400
⇒ AC² = √(400) = 20
∴ Length of each diagonals = 20cm
4. O is an external point of ∆ABC. Show that 2( OA + OB+OC) > AB + BC + CA.

Ans: ∆ABC, ‘O’ An external point
2(OA + OB + OC) > AB + BC + CA
Now, ∆ΟΑΒ OA + OB > AB ………….. (i)
∆ОАС OA + OC > AC ………. (ii)
∆ΟΑΒΒC OB + OC > BC ……….. (iii)
From eqn (1), (2) and (3) we get, 2(OA + OB + OC) > AB + BC + CA
5. Will the sides of the following measures from right angled triangle?
(a) 5, 12, 13
Ans: 5, 12, 13,
∴ 5² + 12² = 13²
⇒ 169 = 169
⇒ 25 + 144
= 169
(b) 3, 4, 5
Ans: 3, 4, 5
∴ 3² + 4² = 5 2
⇒ 9 + 16 = 25°
⇒ 25 = 25
(c) 6, 8, 10
Ans: 6, 8, 10
∴ 6² + 8² = 10²
⇒ 36 + 64 = 100
⇒ 100 = 100
(d) 6, 7, 8
Ans: 6, 7, 8
∴ 6² + 7² = 8²
⇒ 36 + 49 = 64
⇒ 85 ≠ 64
∴ (a), (b), (c) the sides of measures from right angled ∆.
6. Is it possible to four traingles with sides of the following measures?
(a) 3 cm., 4 cm, 5 cm.
Ans: We know that the sum of two sides of a triangle is greater than the third side.
Now, (a) 3 cm. + 4 cm.
= 7 cm. > 5 cm.
∴ A triangle can be obtained with the given measurements.
(b) 5 cm, 7 cm., 12 cm.
Ans: 5 cm. + 7 cm. = 12 cm.
∴ A triangle cannot be found with the given measurements.
(c) 3.4 cm., 2 cm., 5.8 cm.
Ans: 3.4 cm + 2 cm = 5.4 cm ≯ 5.8 cm
∴ A triangle cannot be found with the given measurements.
(d) 6 cm., 7 cm., 14 cm.
Ans: 6 cm + 7 cm = 13 cm ≯ 14 cm
∴ A triangle cannot be found with the given measurements.
7. Prove that in a quadrilateral ABCD.(AB + BC + CD + DA) > (AC + BD)

Ans: given,
ABCD is a quadrilateral.
We know it
The measures of two sides of a triangle are larger than the third side.
∴ From ∆ABC
AB + BC > AC → (i)
Again, ∆ABD
AD + AB > BD → (ii)
From, ∆ADC
AD + CD > AC → (iii)
And from ∆BDC
BC + CD > BD → (iv)
Now, (i) + (ii) + (iii) + (iv)
⇒ AB + BC + AD + AB + AD + CD + BC + CD > AC + BD + AC + BD
⇒ 2AB + 2BC + 2AD + 2CD > 2AC + 2BD
⇒ 2(AB + BC + AD + CD) > 2(AC + BD)
∴ AB + BC + AD + CD > AC + BD
Exercise – 6.5 |
|---|
Find out the correct answers for Q. No. 1 to Q. No. 12.
Q. 1. Value of x in the adjoining triangle is-

(a) 40°
(b) 60°
(c) 35°
(d) 180°
Ans: (b) 60°
2. Value of ‘x’ in the adjoining figure is–
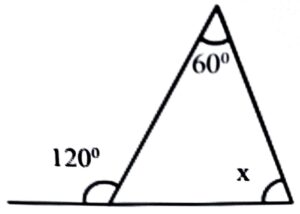
(a) 180°
(b) 55°
(c) 90°
(d) 60°
Ans: (d) 60°
3. In ∆ABC, if ∠A = 35°, ∠B = 65° then ∠C is
(a) 50°
(b) 80°
(c) 30°
(d) 60°
Ans: (b) 80°
4. Hypotenuse of a right-angled triangle is 17cm. If one side is measures 8 cm, then the measure of the third side is-
(a) 15 cm
(b) 12 cm
(c) 13 cm
(d) 25 cm
Ans: (a) 15 cm
5. In ∆ABC if ∠A = 72°, ∠B = 63° then ∠C is
(a) 45°
(b) 80°
(c) 30°
(d) 60°
Ans: (a) 45°
6. In a right-angled triangle, one of the acute angles is 36° then the other acute angle is-
(a) 55°
(b) 54°
(c) 51°
(d) 52°
Ans: (b) 54°
7. The value of ‘x’ in the adjoining figure is-
(a) 5 cm
(b) 7 cm
(c) 3 cm
(d) 4 cm
Ans: (a) 5 cm
৪. The value of ‘x’ in the figure is-

(a) 15 cm
(b) 17cm
(c) 13 cm
(d) 14 cm
Ans: (b) 17 cm
9. In a right-angled triangle ABC, if ∠C = 90°, AC = 5cm, BC = 12 cm then AB is-
(a) 7 cm
(b) 17 cm
(c) 13 cm
(d) 14 cm
Ans: (c) 13 cm
10. In triangle PQR, if ∠P = 90°, PQ = 3 cm, PR = 4 cm, then QR is-
(a) 7 cm
(b) 17 cm
(c) 5 cm
(d) 13 cm
Ans: (c) 5 cm
11. The value of ‘x’ in the figure is-
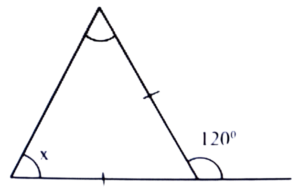
(a) 90°
(b) 60°
(c) 80°
(d) 40°
Ans: (b) 60°
12. Pythagoras Property is satisfied if the triangle is…
(a) Obtuse-angled.
(b) Right-angled.
(c) Acute-angled.
Ans: (b) Right-angled.
Class 7 Mathematics
Chapter – 6 Ospin Academy
The triangle and its properties
|
Exercise – 6.1 |
|---|
1. How many medians are there in a triangle?
Ans: Three medians are there in a triangle.
2. How many altitudes are there in a triangle?
Ans: Three altitudes are there in a triangle.
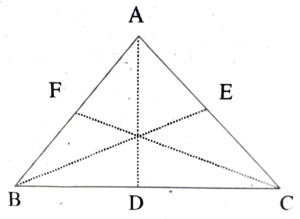
3. Draw a triangle and display its medians.
Ans: AD. BE and CF are three medians in a triangle.
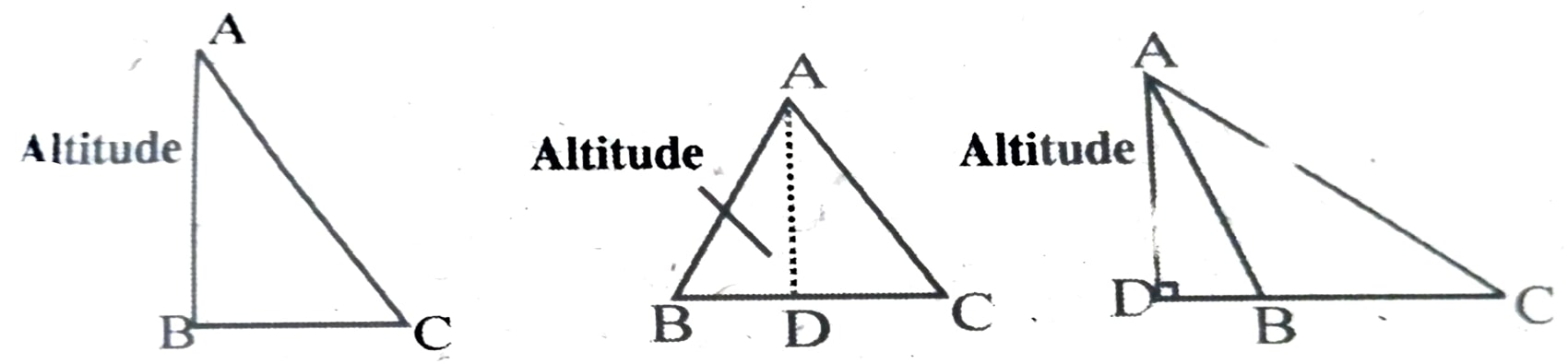
4. Draw a triangle and display its altitudes.
Ans:
5. Name the angle opposite to side LM in ΔLMN.
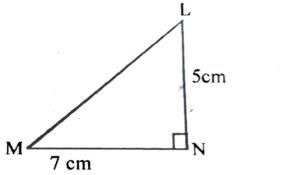
Ans: The angle opposite to side LM in Δ LMN is ∠LNM.
6. Name the side opposite to vertex Q of Δ PQR.
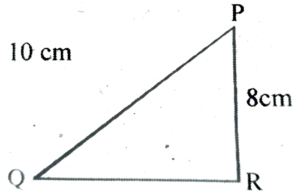
Ans: The side opposite to vertex Q of ΔPQR is PR.
7. Name the vertex opposite to side RT of ΔRST.
Ans: The vertex opposite to side RT of ΔRST is S.
8. (i) Tick (√) the correct answer.
In ∆PQR, PM is-
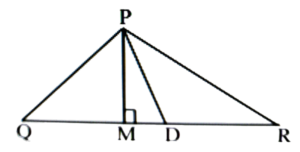
(a) A median
(b) An altitude
(c) A bisector of QR
(d) A side
Ans: (b) An altitude.
(ii) If D is the midpoint of side QR of ∆PQR, then PD is-

(a) perpendicular bisector on QR.
(b) altitude.
(c) median.
(d) opposite side of QR.
Ans: (c) Median.
|
Exercise – 6.2 |
|---|
1. Fill in the blanks:
(a) The angles in the interior of a triangle are called _____________.
Ans: Interior angles.
(b) The angles exterior to a triangle are called.
Ans: Exterior angles.
2. Find the value of x from the diagrams given below:

Ans: ∠x = 50° + 70° = 120°
(b)
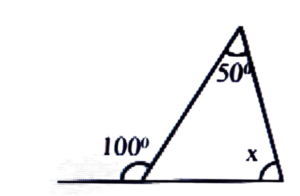
Ans: x + 50° = 100°
⇒ x = 100° – 50° = 50°
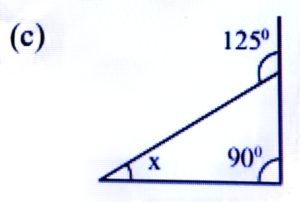
Ans: x + 90° = 125°
⇒ x = 125° – 90° = 35°

Ans: x + 30° = 120°
⇒ x = 120° – 30° = 90°
(e)
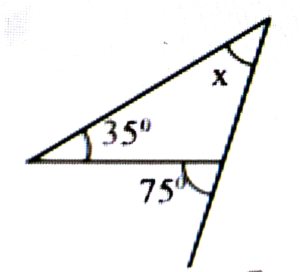
Ans: x + 35° = 75°
⇒ x = 75° – 35° = 40°
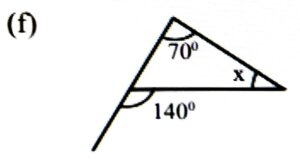
Ans: x + 70° = 140°
⇒ x = 140° – 70° = 70°
3. In a triangle, an exterior angles is 70° and one of its interior opposite angles is 25 deg. Find the value of the other interior opposite angle.
Ans:
70° = x + 25°
⇒ x = 70° – 25°
= 45°
4. Two remote interior angles of a triangle are 60 deg and 80°. Find the value of the exterior angle.
Ans:
∠PRS = ∠P + ∠Q
= 60° + 80°
= 140°
5. In a triangle, an exterior angles is 114° and one of its interior opposite angle is 25° Find the value of other distant interior angle.
Ans:
∠ACD = ∠A + ∠B
⇒ 114° = ∠A + 25°
⇒ ∠A = 114° – 25°
⇒ ∠A = 89°
6. Two remote interior angles of an exterior angle of a triangle are 49º and 41°. Find the value of the exterior angle. (Remote interior angles are also called opposite angles).
Ans:
∠P + ∠Q = ∠PRS
⇒ 49° + 41° = ∠PRS
⇒ ∠PRS = 90°
|
Exercise – 6.3 |
|---|
1. Find the value of x from the figs given below.
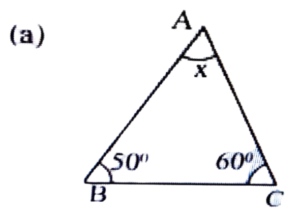
Ans: x + 50° + 60° = 180°
⇒ x = 180° – 110° = 70°

Ans: x + 90° + 30° = 180°
⇒ x = 180°- 120° = 60°
Ans: ∵ Isosceles triangle
∴ ∠A = ∠C = 45°
∴ ∠A + ∠B + ∠C = 180°
⇒ 45° + x + 45° = 180°
⇒ x = 180° – 90° = 90°
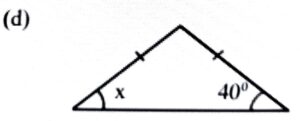
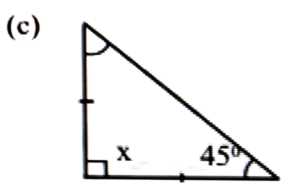
Ans: ∵ Isosceles triangle x = 40°

Ans: ∵ ∆ABC is an isosceles right angled triangle
∴ AB = CB
∠A = ∠C = 45°
⇒ x = 45°
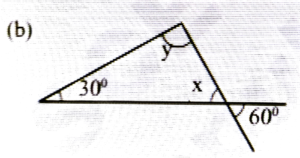
2. Find the values of x and y from the figs given below:
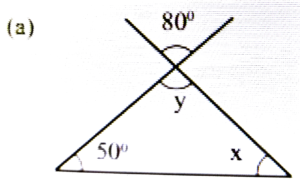
Ans: y = 80° [∴ Vertically opp. angles]
∴ x + 50° + y = 180°
⇒ x + 50° + 80° = 180°
⇒ x + 180° – 130° = 50°
Ans: y = 60° [Vertically opp. angles]
Now, x + y + 300 = 180°
⇒ 60° + y + 30° = 180°
⇒ y = 180° – 90° = 90°
(c)
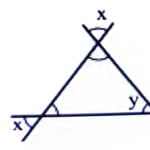
Ans: All three triangles have equal angles
∴ x + x + x = 180° [∴ x = y]
⇒ 3x = 180°
∴ x = 180°/3 = 60°
⇒ y = 60°
3. In a triangle, the measure of one angle is 60°. What will be the measure of the other two angles?
(a) 50°, 40°
Ans: 150° + 40° + 60° = 150° ≠ 180°
(b) 40°, 60°
Ans: 40° + 60° + 60° = 160° ≠ 180°
(c) 60°, 70°
Ans: 60° + 70° + 60° = 190° ≠ 180°
(d) 50°, 70°
Ans: 50° + 70° + 60° = 180°
∴ 50°, 70°
4. Find the value of ∠P from the figures given below-
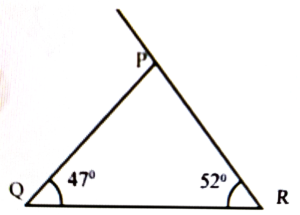
Ans: ∠P = 52° + 47° = 99°
5. Two angles of a triangle are 30° and 80°. Find the measure of the third angle.
Ans: Let the third angle is x°
∴ x° + 30° + 80° = 180°
⇒ x° = 180° – 110° = 70°
6. One angle of a triangle is 80° and the other two angles are equal. What are the measures the other tow angles?
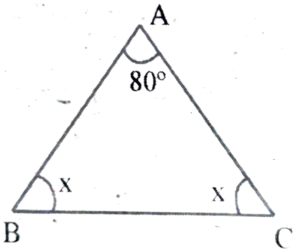
Ans: One angle of a triangle is 80° and the other two angles are equal.
(Let ∠B = ∠C = X )
∴ ∠A + ∠ B + ∠C = 180°
⇒ 80° + ∠B + ∠C = 180°
⇒ 80° + x + x = 180°
⇒ 2x = 180° – 80° = 100°
⇒ x = (100°/2) = 50°
∴ ∠B = ∠C = 50°
7. The ratio of three angles of a triangle is 1:2:1. Find the measures of the angles.
Ans: The ratio of three angles of a triangle is 1:2:1, let three angles are x, 2x and x.
∴ x + 2x + x = 180°
⇒ 4x = 180°
⇒ x = (180°)/4 = 45°
∴ The measure of the angles are 45°, 90°, 45°.
8. The angles of a triangle are (x + 21°) (x – 20°) and (2x – 45°) Find x.
Ans: Three angles of a Delta are, (x + 21°), (x – 20°) আৰু (2x – 45°)
∴ (x + 21°) + (x – 20°) + (2x – 45°) = 180°
⇒ 4x + (21°- 20°- 45°) = 180°
⇒ 4x = 180° + 44°
⇒ 4x = 224°
∴ x = 224°/4 = 56°
x = 56°
9. The ratio of three angles of a traingle is 1:2:3. Find the measures of the angles.
Ans: The ratio of three angles of a triangle is 1:2:3. Let three measures of angles are x, 2x, 3x.
∴ x + 2x + 3x = 180°
⇒ 6x = 180°
⇒ x = 180°/6 = 30°
∴ The measures of the angles are 30°, 60° and 90°.
10. In ∆ ABC, ∠A + ∠B = 116°, ∠B + ∠C = 126 ° Find out the measures of the interior angles of the triangle.
Ans: ∴ ∠A + ∠B + ∠C = 180°
⇒ 116° + ∠C = 180°
⇒ ∠C = 180° – 116 ° = 64°
∴ ∠B + ∠C = 126°
⇒ ∠B + 64° = 126°
⇒ ∠B = 126° – 64° = 62°
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 62° + 64° = 180°
⇒ ∠A + 126° = 180°
⇒ ∠A = 180° – 126° = 54°
∴ ∠A = 54°, ∠B = 62° আৰু ∠C = 64°
11. In ∆ABC, 2 ∠A = 3 ∠B = 6 ∠C. Find out ∠A, ∠B, ∠C
Ans: ∆ABC,2 ∠A = 3 ∠B = 6 ∠C
Now, 3 ∠B = 6 ∠C
⇒ ∠B = 6/3 ∠C = 2 ∠C
2∠A = 6∠C
∴ ∠A = 6/2 ∠C = 3 ∠C
Now, ∠A + ∠B + ∠C = 180°
⇒ 3 ∠C + ∠A + ∠C = 180°
⇒ 6 ∠C = 180°
⇒ ∠C = 30°
∴ ∠A = 3 × 30° = 90°
∠B = 2 × 30° = 60°
∠C = 30°
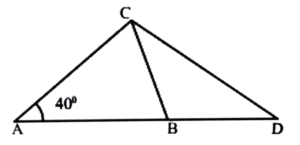
12. In the figure given below ∠CAB = 40°, AC = AB and BC = BD Find out
(a) ∠ACB and
(b) ∠CDB
Ans: In the figure, ∠CAB = 40°
AC = AB
∴ ∠C = ∠B
Now, ∠A + ∠B + ∠C = 180°
⇒ 40° + 2 ∠B = 180°
⇒ 2 ∠B = 180° – 40°
∴ ∠B = 140°/2 = 70°
∴ ∠C = 70°
∴ ∠CBD = 40° + 70° = 110°
That, ∠ACB = 70°
Again, BC = BD
∴ ∠BCD = ∠CDB
∴ ∆BCD get from, ∠CBD + ∠BCD + ∠CDB = 180°
⇒ ∠110° + 2 ∠CDB = 180°
⇒ 2180° CDB = 180° – 110°
⇒ ∠CDB = 70°
∴ ∠CDB = 70°/2 = 35°
∴ (a) ∠ACB = 70°, (b) ∠CDB = 35°
Exercise – 6.4 |
|---|
1. In the following figure AB = 10cm AC = 17cm and AD = 8cm. Determine BC.
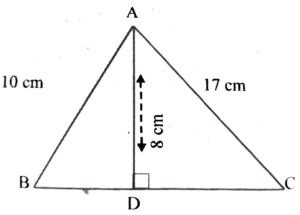
Ans: In the figure, AB = 10 cm
BC = 17 cm and AD = 8 cm
∴ BD² = AB² – AD²
= 100² – 8² = 100 – 64 = 36
![]()
∴ CD = BC – BD = (17 – 6) cm = 11 cm
∴ AC² = AD² + CD²
= 8² + 11² = 64 + 121 = 185
![]()
2. In the perimeter of a triangle is 15 cm and two sides are 5 cm and 7 cm then what is the length of the third side.
Ans: Perimeter = 15cm, two sides are 5 cm and 7 cm.
∴ Measure of third side
= 15 – (5 + 7) cm
= (15-12) cm
= 3cm.
3. In a rectangle the lengths of two adjacent sides are 16 cm and 12 cm. Find out the lengths of two diagonals.
Ans: AD = 16cm,
CD = 12cm
∴ ∆ACD-[In ∆ACD ]
AC² = AD² + CD²
⇒ AC² = 16² + 12²
⇒ AC² = 256 + 244 = 400
⇒ AC² = √(400) = 20
∴ Length of each diagonals = 20cm
4. O is an external point of ∆ABC. Show that 2( OA + OB+OC) > AB + BC + CA.

Ans: ∆ABC, ‘O’ An external point
2(OA + OB + OC) > AB + BC + CA
Now, ∆ΟΑΒ OA + OB > AB ………….. (i)
∆ОАС OA + OC > AC ………. (ii)
∆ΟΑΒΒC OB + OC > BC ……….. (iii)
From eqn (1), (2) and (3) we get, 2(OA + OB + OC) > AB + BC + CA
5. Will the sides of the following measures from right angled triangle?
(a) 5, 12, 13
Ans: 5, 12, 13,
∴ 5² + 12² = 13²
⇒ 169 = 169
⇒ 25 + 144
= 169
(b) 3, 4, 5
Ans: 3, 4, 5
∴ 3² + 4² = 5 2
⇒ 9 + 16 = 25°
⇒ 25 = 25
(c) 6, 8, 10
Ans: 6, 8, 10
∴ 6² + 8² = 10²
⇒ 36 + 64 = 100
⇒ 100 = 100
(d) 6, 7, 8
Ans: 6, 7, 8
∴ 6² + 7² = 8²
⇒ 36 + 49 = 64
⇒ 85 ≠ 64
∴ (a), (b), (c) the sides of measures from right angled ∆.
6. Is it possible to four traingles with sides of the following measures?
(a) 3 cm., 4 cm, 5 cm.
Ans: We know that the sum of two sides of a triangle is greater than the third side.
Now, (a) 3 cm. + 4 cm.
= 7 cm. > 5 cm.
∴ A triangle can be obtained with the given measurements.
(b) 5 cm, 7 cm., 12 cm.
Ans: 5 cm. + 7 cm. = 12 cm.
∴ A triangle cannot be found with the given measurements.
(c) 3.4 cm., 2 cm., 5.8 cm.
Ans: 3.4 cm + 2 cm = 5.4 cm ≯ 5.8 cm
∴ A triangle cannot be found with the given measurements.
(d) 6 cm., 7 cm., 14 cm.
Ans: 6 cm + 7 cm = 13 cm ≯ 14 cm
∴ A triangle cannot be found with the given measurements.
7. Prove that in a quadrilateral ABCD.(AB + BC + CD + DA) > (AC + BD)

Ans: given,
ABCD is a quadrilateral.
We know it
The measures of two sides of a triangle are larger than the third side.
∴ From ∆ABC
AB + BC > AC → (i)
Again, ∆ABD
AD + AB > BD → (ii)
From, ∆ADC
AD + CD > AC → (iii)
And from ∆BDC
BC + CD > BD → (iv)
Now, (i) + (ii) + (iii) + (iv)
⇒ AB + BC + AD + AB + AD + CD + BC + CD > AC + BD + AC + BD
⇒ 2AB + 2BC + 2AD + 2CD > 2AC + 2BD
⇒ 2(AB + BC + AD + CD) > 2(AC + BD)
∴ AB + BC + AD + CD > AC + BD
Exercise – 6.5 |
|---|
Find out the correct answers for Q. No. 1 to Q. No. 12.
Q. 1. Value of x in the adjoining triangle is-

(a) 40°
(b) 60°
(c) 35°
(d) 180°
Ans: (b) 60°
2. Value of ‘x’ in the adjoining figure is–
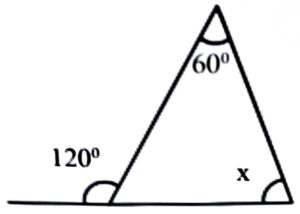
(a) 180°
(b) 55°
(c) 90°
(d) 60°
Ans: (d) 60°
3. In ∆ABC, if ∠A = 35°, ∠B = 65° then ∠C is
(a) 50°
(b) 80°
(c) 30°
(d) 60°
Ans: (b) 80°
4. Hypotenuse of a right-angled triangle is 17cm. If one side is measures 8 cm, then the measure of the third side is-
(a) 15 cm
(b) 12 cm
(c) 13 cm
(d) 25 cm
Ans: (a) 15 cm
5. In ∆ABC if ∠A = 72°, ∠B = 63° then ∠C is
(a) 45°
(b) 80°
(c) 30°
(d) 60°
Ans: (a) 45°
6. In a right-angled triangle, one of the acute angles is 36° then the other acute angle is-
(a) 55°
(b) 54°
(c) 51°
(d) 52°
Ans: (b) 54°
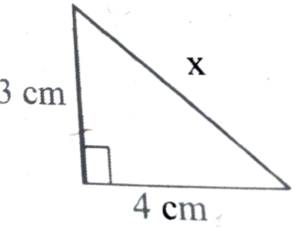
7. The value of ‘x’ in the adjoining figure is-
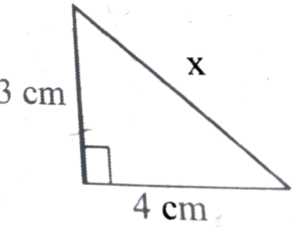
(a) 5 cm
(b) 7 cm
(c) 3 cm
(d) 4 cm
Ans: (a) 5 cm
৪. The value of ‘x’ in the figure is-

(a) 15 cm
(b) 17cm
(c) 13 cm
(d) 14 cm
Ans: (b) 17 cm
9. In a right-angled triangle ABC, if ∠C = 90°, AC = 5cm, BC = 12 cm then AB is-
(a) 7 cm
(b) 17 cm
(c) 13 cm
(d) 14 cm
Ans: (c) 13 cm
10. In triangle PQR, if ∠P = 90°, PQ = 3 cm, PR = 4 cm, then QR is-
(a) 7 cm
(b) 17 cm
(c) 5 cm
(d) 13 cm
Ans: (c) 5 cm
11. The value of ‘x’ in the figure is-
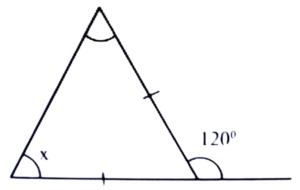
(a) 90°
(b) 60°
(c) 80°
(d) 40°
Ans: (b) 60°
12. Pythagoras Property is satisfied if the triangle is…
(a) Obtuse-angled.
(b) Right-angled.
(c) Acute-angled.
Ans: (b) Right-angled.
1. What topics are covered in SEBA Class 7 Maths Chapter 6 Triangle and Its Properties?
This chapter covers key topics such as types of triangles, triangle inequalities, medians and altitudes, the sum of angles in a triangle, Pythagoras theorem, and more.
2. How many exercises are there in Chapter 6 Triangle and Its Properties?
There are five exercises in this chapter: Exercises 6.1, 6.2, 6.3, 6.4, and 6.5. Each exercise focuses on different properties of triangles.
3. Are step-by-step solutions available for all exercises?
Yes, we provide detailed step-by-step solutions for all five exercises to help students understand each concept easily.
4. What is the importance of the Pythagoras theorem in this chapter?
The Pythagoras theorem is an important concept covered in this chapter, which helps in solving problems related to right-angled triangles.
5. Are these solutions available in English Medium?
Yes, all solutions for SEBA Class 7 Maths Chapter 6 are available in English Medium, following the SCERT Assam syllabus.
