SEBA Class 7 Maths Chapter 9 Rational Numbers Solutions | SCERT Assam | Exercises 9.1 & 9.2 | QR Code: Z9U7W3

SEBA Class 7 Maths Chapter 9 Rational Numbers Solutions | SCERT Assam | Exercises 9.1 & 9.2

Find SEBA Class 7 Maths Chapter 9 Rational Numbers Solutions for Exercises 9.1, 9.2 in English Medium, following the SCERT Assam syllabus. This chapter covers important topics such as properties of rational numbers, operations on rational numbers, representation of rational numbers on a number line, and their real-life applications. Our detailed step-by-step solutions make it easy for students to understand and solve problems effectively. QR Code: Z9U7W3 for quick access.

📚 Get Complete SEBA Class 7 Maths Solutions – Access step-by-step solutions for all chapters as per the SCERT Assam syllabus.

➡ Click here for full subject solutions

Rational Numbers

Exercise 9.1

1. Select the correct options from the following sentences –

(i) All natural numbers are integers.

Ans: True.

(ii) An integer may not be a natural number.

Ans: True.

(iii) If a number is rational then the number must be an integer.

Ans: True.

(iv) There are infinite numbers of rational numbers between two integers.

Ans: True.

(v) All fractions are integers.

Ans: False.

(vi) All fractions are rational numbers.

Ans: True.

(vii) 0 is a rational number.

Ans: True.

(viii) Each integer is rational.

Ans: True.

2. Write 3 equal rational numbers for the following fractions. (Keep in mind that there are infinite numbers of equivalent rational number for every number)

(i) -4/5

Ans: – 4/5 = (-4 × 2)/(5 × 2) = -8/10

-4/5 = (-4 × 3)/(5 × 3) = -12/15

-4/5 = (-4 × 4)/(5 × 4) = -16/20

(ii) 2/-3

Ans: 2/-3 = (2 × 2)/(-3 × 2) = -4/6

2/-3 = (2 × 2)/(-3 × 2) = -6/9

2/-3 = (2 × 4)/(-3 × 4) = -8/12

(iii) -7/21

Ans: -7/21 = -7 ÷ 7/21 ÷ 7 = -1/3

-7/21 = (-7 × 2)/(21 × 2) = -14/42

-7/21 = (-7 × 3)/(21 × 13) = -21/63

(iv) 1/-9

Ans: 1/-9 = (1 × 2)/(-9 × 2) = 2/-18

1/-9 = (1 × 3)/(-9 × 3) = -3/27

1/-9 = (1 × 4)/(-9 × 4) = -4/36

(v) 40/64

Ans: 40/64 = (40 ÷ 2)/(64 ÷ 2) = 20/30

40/64 = (40 ÷ 4)/(64 ÷ 4) = 10/16

40/64 = (40 ÷ 8)/(64 ÷ 8) = 5/8

3. Are the following pairs equal?

(i) -3/13, 6/-26

Ans: Yes.

(ii) 7/-3, 1/-3

Ans: No.

4. Replace x and y in such a way so that the equity exists.

(i) 9/-40 = -9/x

Ans: x = 40

(ii) -5/35 = y/-70

Ans: y = 10

5. Express in standard form.

(i) 5/-2

Ans: 5/-2 = -2 1/2

(ii) 7/-14

Ans: 7/-14 = 7/(-7 × 2) = -1/2

(iii) 25/-45

Ans: 25/-45 = (5 × 5)/(-5 × 9) = -5/9

(iv) 2 3/7

Ans: 2 3/7

(v) -18/10

Ans: -18/10 = (-2 × 9)/(2 × 5) = -9/5

6. Which is smaller in each of the pair of the following rational numbers.

(a) 7/14, -2/4

Ans: 7/14 = (7 × 2)/(14 × 2) = 14/28

-2/4 = (-2 × 7)/(4 × 7) = -14/28

∴ -2/4 Smaller Number.

(b) -1/3, -2/5

Ans: -1/3 = (-1 × 5)/(3 × 5) = -5/15

-2/5 = (-2 × 3)/(5 × 3) = -6/15

∴ -6/15 < -5/15

∴ -2/5 < -1/3 ∴ -2/3 Smaller Number.

(c) -8/5, -7/4

Ans: -8/5 = (-8 × 4)/(5 × 4) = -32/20

-7/4 = (-7 × 5)/(4 × 5) = -35/20

Now, -35/20 < -32/20 ∴ -7/4 Smaller Number.

(d) -2/-3, 16/12

Ans: -2/-3 = 2/3 = (2 × 2)/(2 × 3) = 4/6

16/12 = 8/6

∴ -2/-3 Smaller Number.

7. Write 5 rational number between the following pair of numbers. (Keep in mind that there are several rational numbers in each of the following pairs)

(i) -1 and 1

Ans: 5 rational numbers between -1 and 1

Let, a = – 1 b = 1 a < b n = 5

d = 1 – (-1)/(5 + 1) = 2/6 = 1/3

∴ -1 + 1 × 1/3, -1 + 2 × 1/3, -1 + 3 × 1/3, -1 + 4 × 1/3, – 1 × 5 × 1/3

⇒ (-3 + 1)/3, (-3 + 2)/3, -1 + 1, (-3 + 4)/3, (-3 + 5)/3

⇒ -2/3, -1/3, 0, 1/3, 2/3

(ii) -3/4, 3/4

Ans:

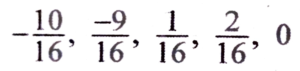
(iii) -3, -2

Ans: The 5 rational numbers between –3 and –2

Are- -2.1, -2.2,-2.3, -2.5.

(iv) -2/5, -2/3

Ans: -2/5, -2/3

Let, a = -2/5, b= -2/3, a < b

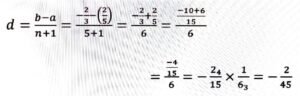
∴ The rational numbers are-

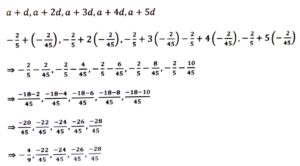
(v) 5/8, 3/7

Ans: 5/8, 3/7

Let, a = 3/7, b = 5/8, a < b

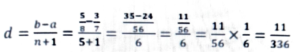
∴ The rational numbers are-

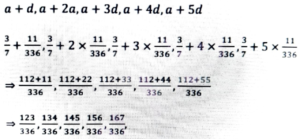
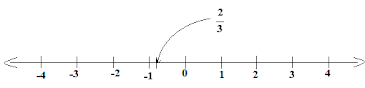
8. Put the following rational numbers in number line –

(i) 2/3

Ans:

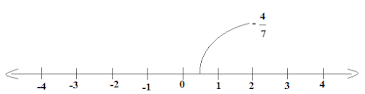
(ii) -4/7

Ans:

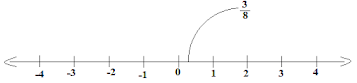
(iii) 3/8

Ans:

(iv) -2 3/5

Ans:

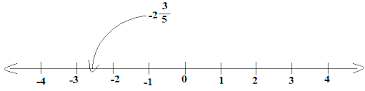
(v) 3 4/9

Ans:

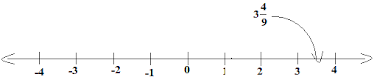
9. 31/5 is a rational lies to the right of 0. What is the rational number which lies at the left of 0 in same distance? What will be the rational number which lies to the centre of the two rational numbers?

Ans: 31/5, 0

10. (i) What will be the greatest integer among the integers which are smaller than ½?

Ans: 0

(ii) What will be the smallest integer among all the integers which are greater than ½?

Ans: 1

Exercise 9.2

1. Find the sum:

(a) 3/6 + 5/3

Ans: 3/6 + 5/3

= (3 + 10)/6 = 13/6

(b) -5/6 + 4/7

Ans: -5/6 + 4/7

= (-35 + 24)/42 = -11/42

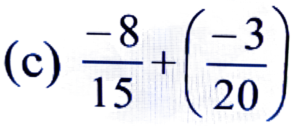
Ans:

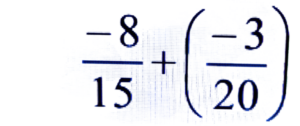
= -8/15 – 3/20

= -32 – 9/60 = -41/60

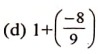
Ans:

= 1 – 8/9

= 9 – 8/9 = 1/9

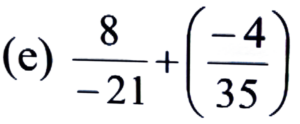
Ans:

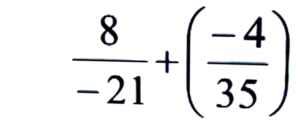
= -8/21 – 4/35

= -40 – 12/105 = -52/105

(f) -3 4/5 + 2 1/6

Ans: -3 4/5 + 2 1/6

= -19/5 + 13/6

= (-114 + 65)/30 = -49/30

Ans:

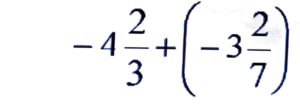
= -14/3 – 23/7 = (-98 – 69)/21 = -167/21 = -7 20/21

2. Subtract the following:

(i) 51/14 – 3/2

Ans: 51/14 – 3/2

= 51 – 21/14

= 30/14 = 15/7 = 2 1/7

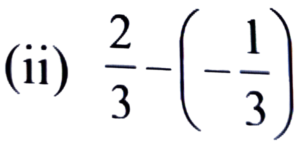
Ans:

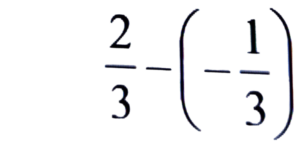
= 2/3 + 1/3

= 2 + 1/3 = 3/3 = 1

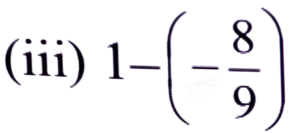
Ans:

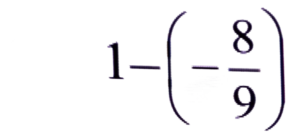
= 1 + 8/9

= 9 + 8/9 = 17/9 = 1 8/9

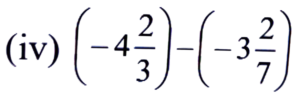
Ans:

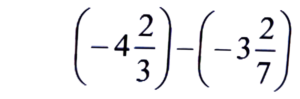
= -14/3 + 23/7

= -98 + 69/21

= -29/21 = -1 8/21

Ans:

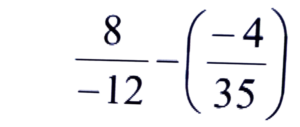
= -8/12 + 4/35 = -2/3 + 4/35

= -70 + 12/105

= -58/105 = -1 58/105

(vi) -2 1/9 -5

Ans: -2 1/9 -5

= -19 – 45/9

= -64/9 = -7 1/9

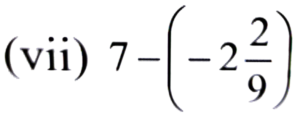
Ans:

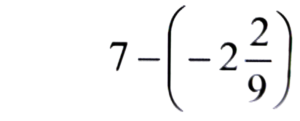
= 7 + 20/9

= (63 + 20)/9 = 83/9 = 9 2/9

3. Find the product:

(i) -15/14 × 2/3

Ans: -15/14 × 2/3

= (-15 × 2)/(14 × 3)

= -30/42 = -5/7

(ii) 3/-11 × -2/5

Ans: 3/-11 × -2/5

= 3 × (-2)/(-11) × 5

= (3 × 2)/(11 × 5) = 6/55

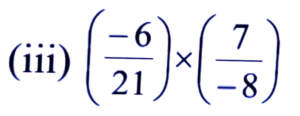
Ans:

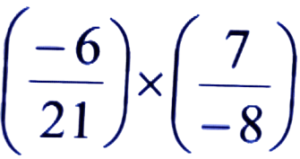
= (-6) × 7/21 × (-8)

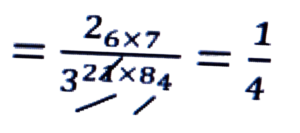
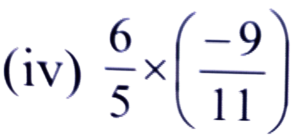
Ans:

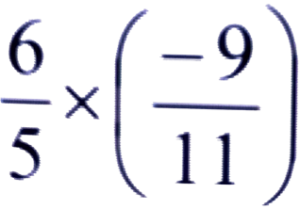
= 6 × (-9)/5 × 11

= -54/55

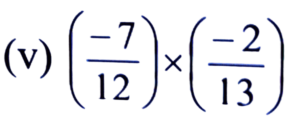
Ans:

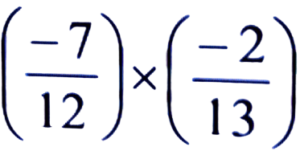
= (-7) × (-2)/12 × 13 = 7 × 2/12 × 13 = 7/6 × 13 = 7/78

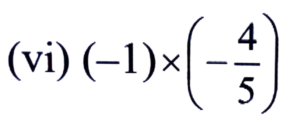
Ans:

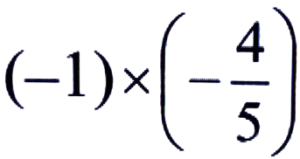
= 4/5

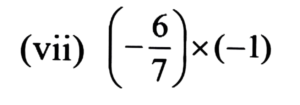
Ans:

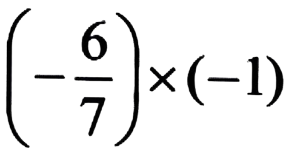
= 6/7

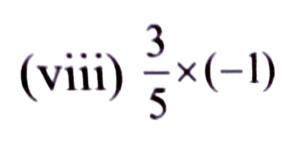
Ans:

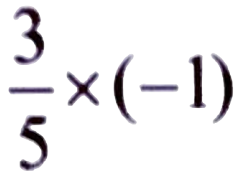
= -3/5

4. Find out the value:

(i) (-5) ÷ (-1)

Ans: (-5) ÷ (-1)

= -5/-1 = 5

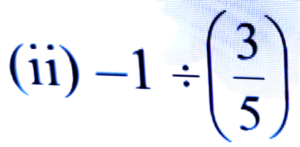
Ans:

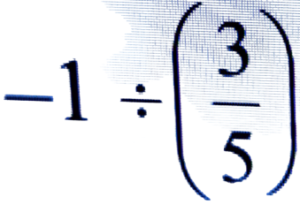
= -1 × 5/3 = -5/3 = -1 2/3

Ans:

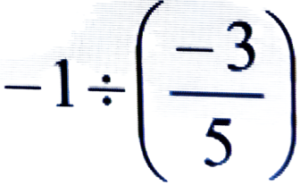
= -1 × (5/-3)

= 5/3 = 1 2/3

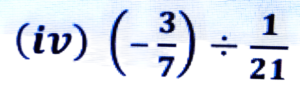
Ans:

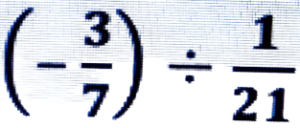
= -3/7 × 21/1 = -9

(v) 7/-3 ÷ (-21)

Ans: 7/-3 ÷ (-21)

= 7/-3 × 1/-21

= 7/3 × 21

= 1/3 × 3 = 1/9

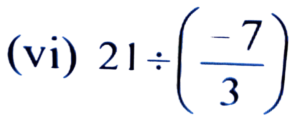
Ans:

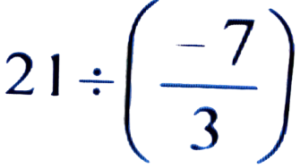
= 21 × 3/-7

= 21 × 3/-7

= -9

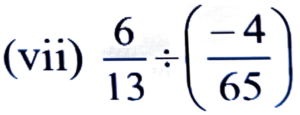
Ans:

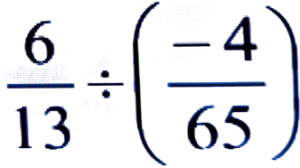
= 6/13 × 65/-4

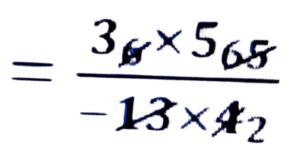
= 3 × 5/2

= -15/2 = -7 1/2

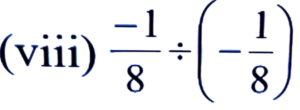
Ans:

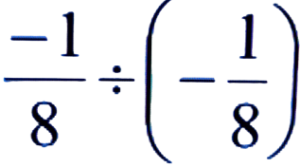
= -1/8 × 8/-1

= 1

5. Answer as per the instruction:

(i) What is Additive inverse of – 8/9.

Ans: 8/9

(ii) What is additive inverse of -1.

Ans: 1

(iii) 2/3 / (2/3) = 1 (Say correct or incorrect).

Ans: 2/3 / (2/3) = 1 [Correct]

(iv) 1 / (4/3) = 3/4 (Say correct or incorrect).

Ans: 1 / (4/3) = 3/4 [Correct].

(v) If a and b are two rational numbers then, a × (- b) = – (a × b) and – a × b = – (a × b) Now take any two rational numbers in place of a and b and verify the above equity.

Ans: Correct.

(vi) What is the reciprocal of – 3/7?

Ans: -3/7

FAQs