SEBA Class 7 Mathematics (Assamese Medium) Chapter 6 – ত্রিভুজ আৰু ইয়াৰ ধর্ম Solutions & Summary
Find SEBA Class 7 Mathematics Chapter 6 – “ত্রিভুজ আৰু ইয়াৰ ধর্ম” (The Triangle and Its Properties) solutions, designed for Assamese medium students. This chapter explains different types of triangles, their properties, and important theorems related to triangles.
Students will learn about the angle sum property, Pythagoras theorem, types of triangles (scalene, isosceles, equilateral, right-angled), and median and altitude of a triangle. The chapter also covers exterior angle property and inequalities in triangles.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students strengthen their understanding of triangles and perform well in exams.
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীনী – 6.1 |
|---|
1. এটা ত্রিভুজৰ মধ্যমা কিমানডাল?
উত্তৰঃ 3 ডাল।
2. এটা ত্রিভুজৰ উন্নতিৰ সংখ্যা কিমান?
উত্তৰঃ 3 ডাল।
3. এটা ত্রিভুজ আঁকা আৰু মধ্যমাবোৰ প্ৰদৰ্শন কৰা।
উত্তৰঃ
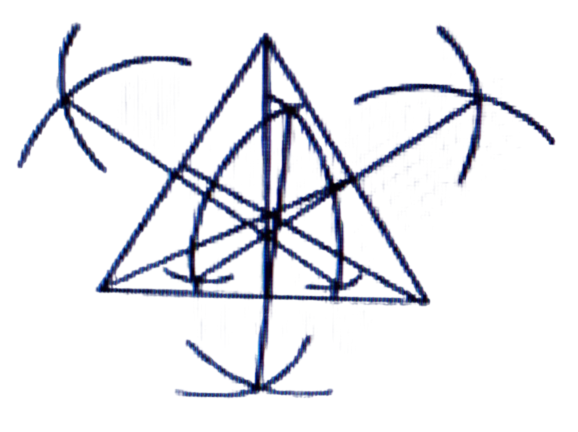
4. এটা ত্রিভুজ আঁকা আৰু উন্নতিবোৰ প্ৰদৰ্শন কৰা।
উত্তৰঃ
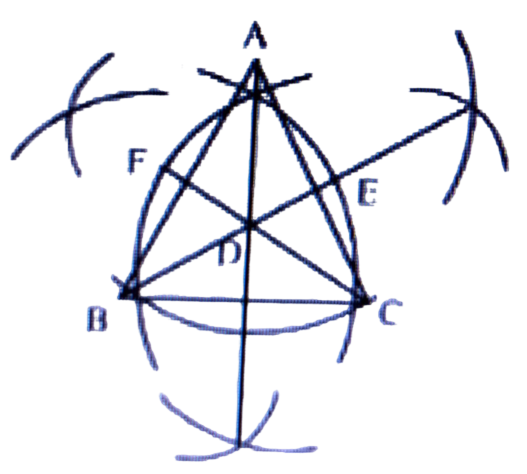
5. ∆LMN ৰ LM বাহুৰ বিপৰীত কোণটো উল্লেখ কৰা।
উত্তৰঃ ∠N
6. ∆PQR ৰ শীর্ষবিন্দু Q ৰ বিপৰীত বাহুটো উল্লেখ কৰা।

উত্তৰঃ PR = 8 চে.মি.।
7. ∆RST ৰ RT বাহুৰ বিপৰীত শীর্ষবিন্দুটো উল্লেখ কৰা।
উত্তৰঃ ∠S
8. শুদ্ধ উত্তৰটোত √ চিন দিয়া।
(ⅰ) ∆PQR ৰ PM এডাল।
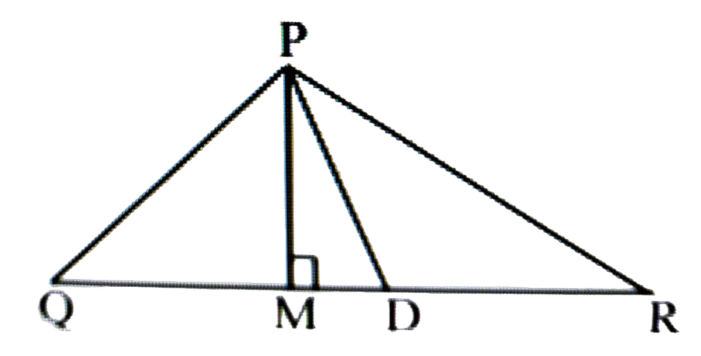
(a) মধ্যমা।
(b) উন্নতি।
(c) QR ৰ সমদ্বিখণ্ডক।
(d) ∆PQR ৰ বাহু।
উত্তৰঃ (b) উন্নতি।
(ii) যদি ∆PQR ৰ QR ৰ মধ্যবিন্দু D হয় তেন্তে PD এডাল

(a) QR ৰ লম্ব সমদ্বিখণ্ডক।
(b) উন্নতি।
(c) মধ্যমা।
(d) QR ৰ বিপৰীত বাহু।
উত্তৰঃ (c) মধ্যমা।
অনুশীলনী – 6.2 |
|---|
1. খালী ঠাই পূৰ কৰা–
(a) ত্রিভুজৰ অন্তৰ্ভাগত থকা কোণবোৰক ______________ বোলে।
উত্তৰঃ ত্রিভুজৰ অন্তৰ্ভাগত থকা কোণবোৰক অন্তঃকোণ বোলে।
(b) ত্রিভুজৰ বহির্ভাগত থকা কোণবোৰক ______________ বোলে।
উত্তৰঃ ত্রিভুজৰ বহির্ভাগত থকা কোণবোৰক বহিঃকোণ বোলে।
2. তলৰ চিত্ৰৰ পৰা x নিৰ্ণয় কৰা।

উত্তৰঃ x = 50° + 70° = 120°
(b)
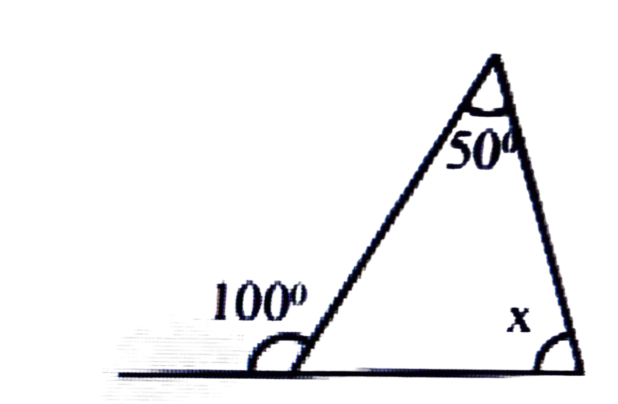
উত্তৰঃ x + 50° = 100°
⇒ x = 100° – 50° = 50°
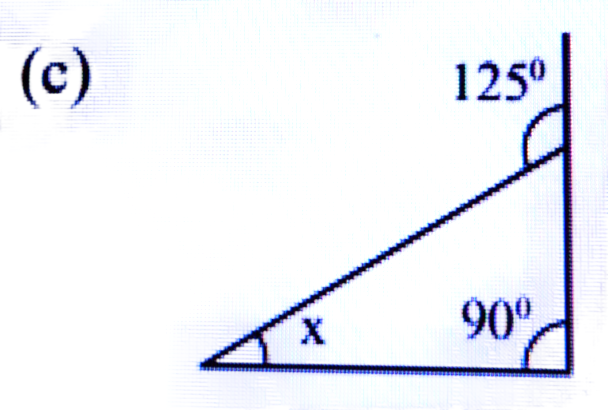
উত্তৰঃ x + 90° = 125°
⇒ x = 125° – 90° = 35°

উত্তৰঃ x + 30° = 120°
⇒ x = 120° – 30° = 90°
(e)
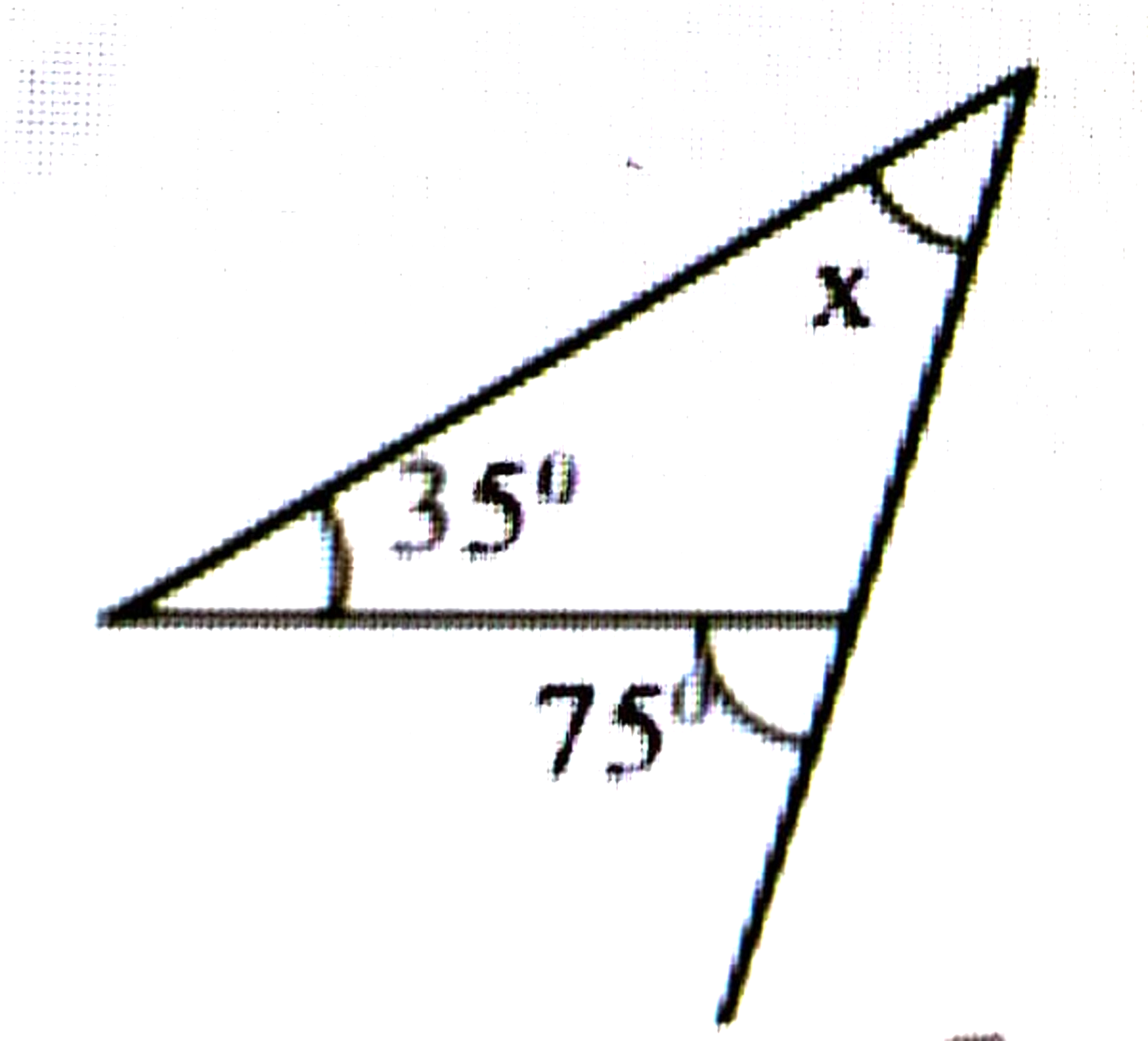
উত্তৰঃ x + 35° = 70°
⇒ x = 75° – 35° = 40°
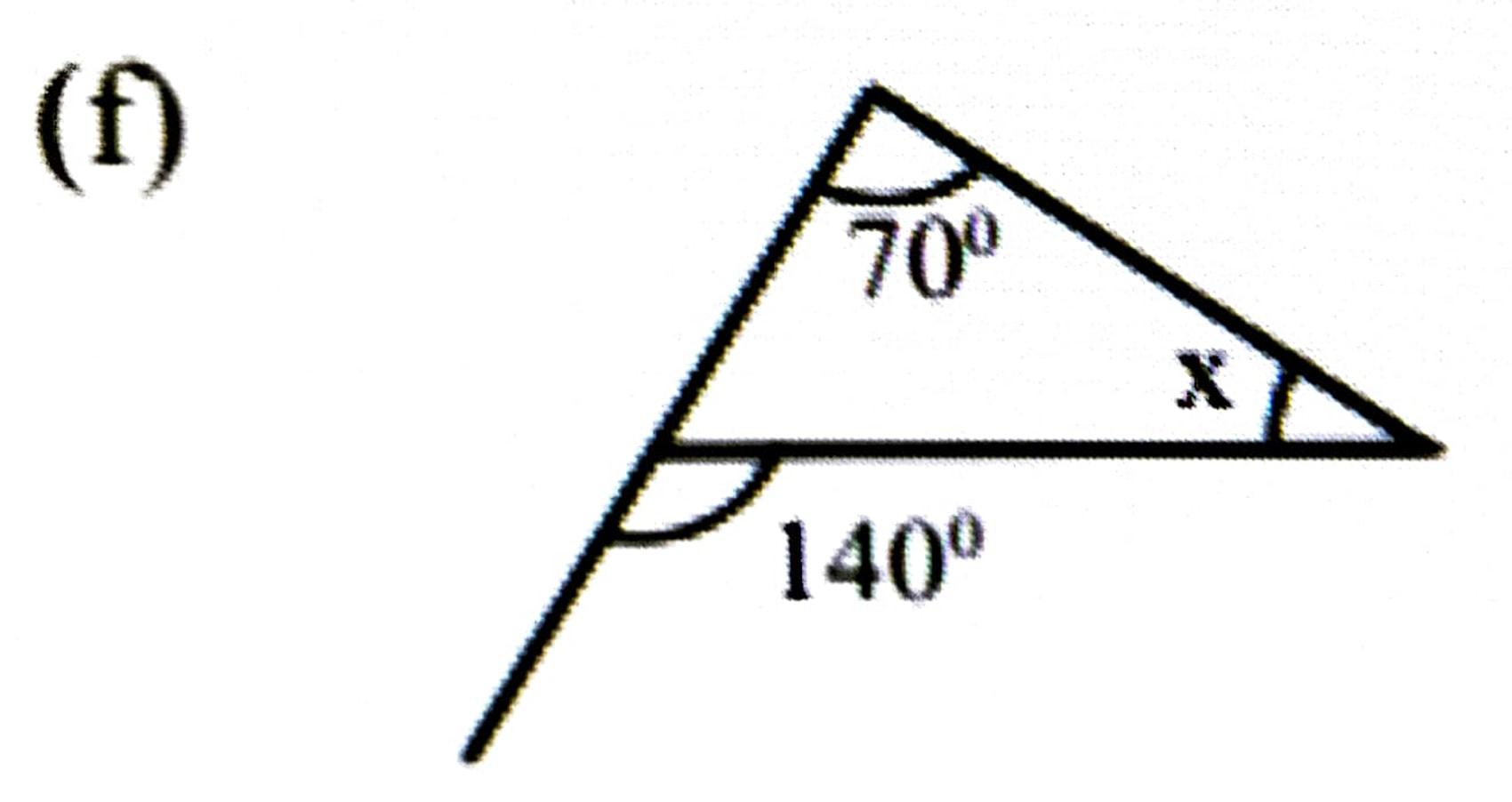
উত্তৰঃ x + 70° = 140°
⇒ x = 140° – 70° = 70°
3. এটা ত্রিভুজৰ এটা বহিঃকোণৰ মাপ 70° আৰু ইয়াৰ দূৰৱৰ্তী অন্তঃকোণ এটাৰ মাপ 25° হ’লে আনটো দূৰৱৰ্তী অন্তঃকোণৰ মাপ কিমান?
উত্তৰঃ ধৰাহ’ল, আনটোত দূৰৱৰ্তী অন্তঃকোণ = x°
∴ x + 25 = 70°
⇒ x = 70° – 25°
= 45°
4. ত্রিভুজ এটাৰ বহিঃকোণৰ দূৰৱৰ্তী অন্তঃকোণ দুটা ক্রমে 60° আৰু 80°। বহিঃকোণটোৰ মাপ কিমান?
উত্তৰঃ দূৰৱৰ্তী অন্তঃকোণ দুটা ক্রমে, 60° আৰু 80°
∴ বহিঃকোণৰ = 60° + 80° = 140°
5. এটা ত্রিভুজৰ এটা বহিঃকোণৰ জোখ 114° আৰু তাৰ এটা দূৰৱর্তী অন্তঃস্থ কোণ 25° হ’লে আনটো দূৰৱৰ্তী অন্তঃস্থ কোণৰ জোখ কিমান?
উত্তৰঃ ধৰাহ’ল, আনটো দূৰৱৰ্তী অন্তঃকোণ x°
∴ x + 25° = 114°
⇒ x = 114°- 25° = 89°
6. এটা ত্রিভুজৰ এটা বহিঃকোণৰ বিপৰীত অন্তঃস্থ কোণ দুটা ক্রমে 49° আৰু 41° হ’লে বহিঃকোণৰ জোখ কিমান? [দূৰৱৰ্তী অন্তঃকোণক বিপৰীত অন্তঃকোণো বোলা হয়]।
উত্তৰঃ বহিঃকোণৰ বিপৰীত অন্তঃস্থ কোণ দুটা ক্রমে, 49° আৰু 41°
∴ বহিঃকোনটোৰ মাপ = 49° + 41° – 90°
অনুশীলনী – 6.3 |
|---|
1. চিত্ৰৰ পৰা x নিৰ্ণয় কৰা।

উত্তৰঃ x + 50° + 60° = 180°
⇒ x = 180° – 110° = 70°

উত্তৰঃ x + 90° + 30° = 180°
⇒ x = 180°- 20° = 60°
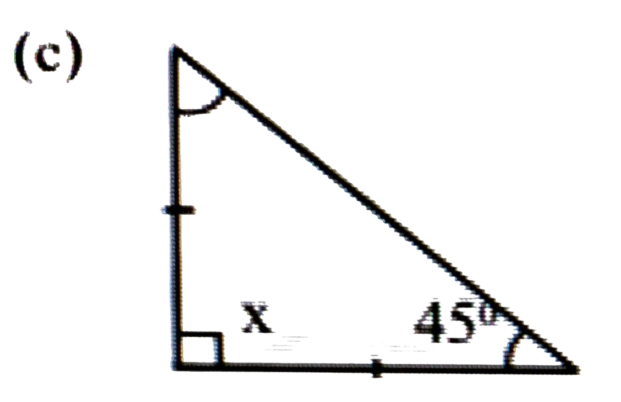
উত্তৰঃ ত্রিভুজ সমদ্বিবাহু সমকোণী ত্রিভুজ সদ্বিবাহু ত্রিভুজটোৰ ভূমি সংলগ্ন কোণৰ মাপ = 45°
∴ সমদ্বিবাহু ত্রিভুজটোৰ আনটো ভূমি সংলগ্ন কোণৰ মাপ = 45°
∴ x = 90° [x + 45° + 45° = 180°]
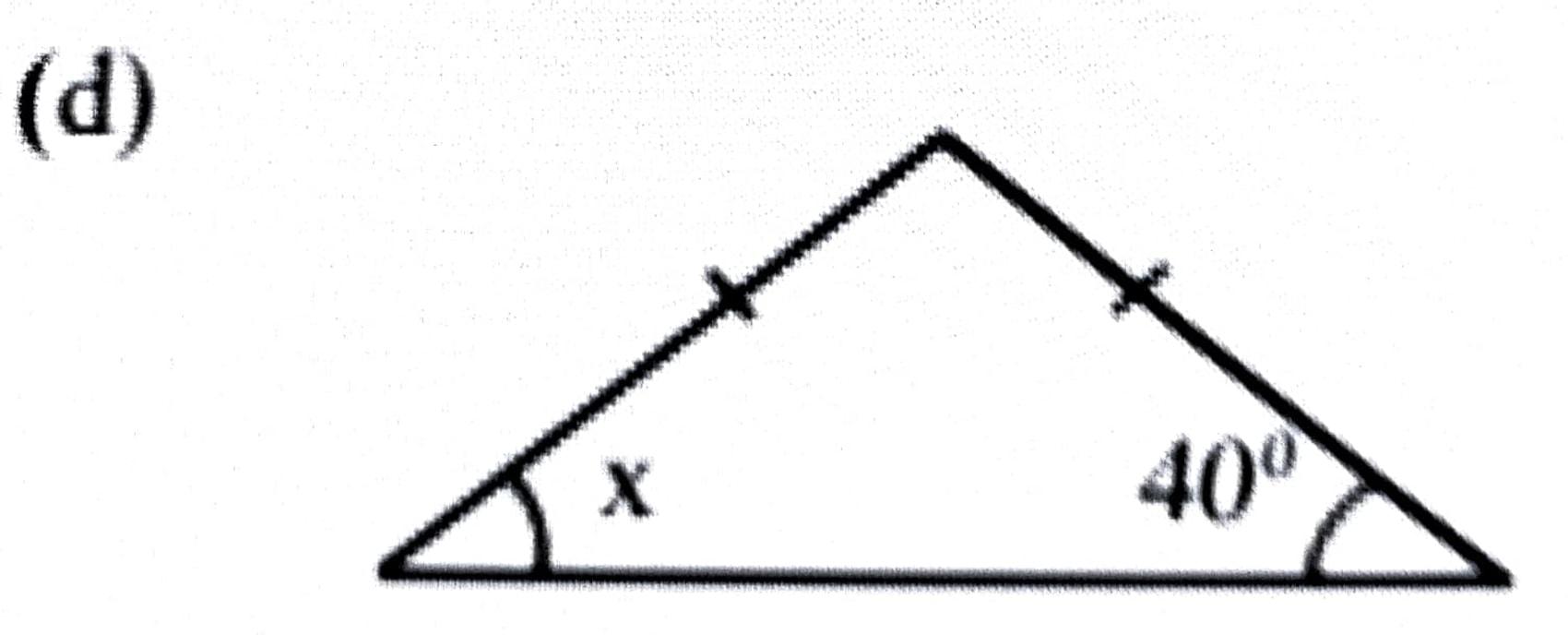
উত্তৰঃ ত্রিভুজটো সমদ্বিবাহু ত্রিভুজ।
∴ x = 40° [∴ ভূমিসংলগ্নকোণদুটাসমান।]

উত্তৰঃ ত্রিভুজটো সমদ্বিবাহু সমকোণী ত্রিভুজ।
∴ x = 45°
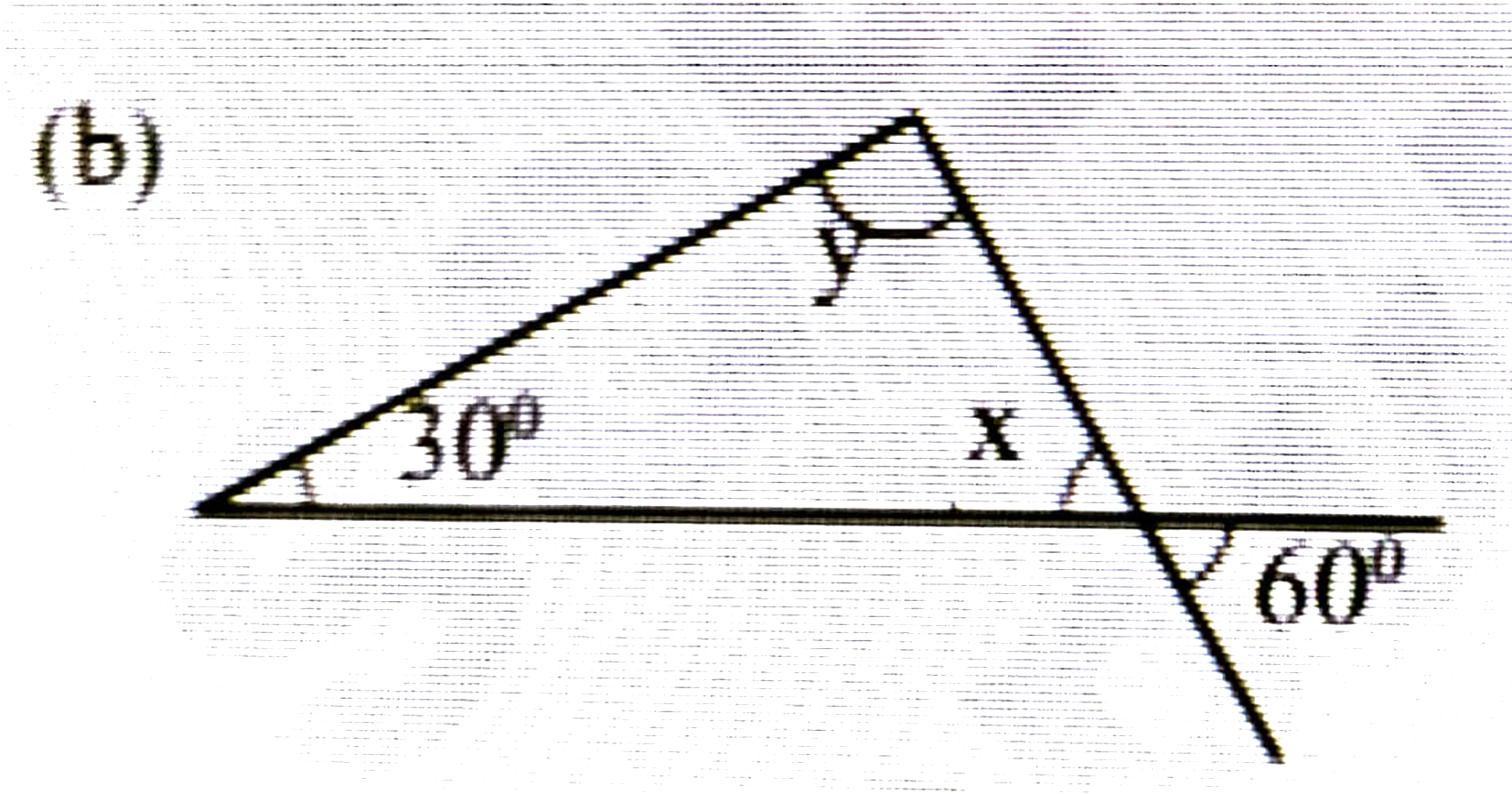
2. চিত্ৰৰ পৰা x আৰু y নিৰ্ণয় কৰা।
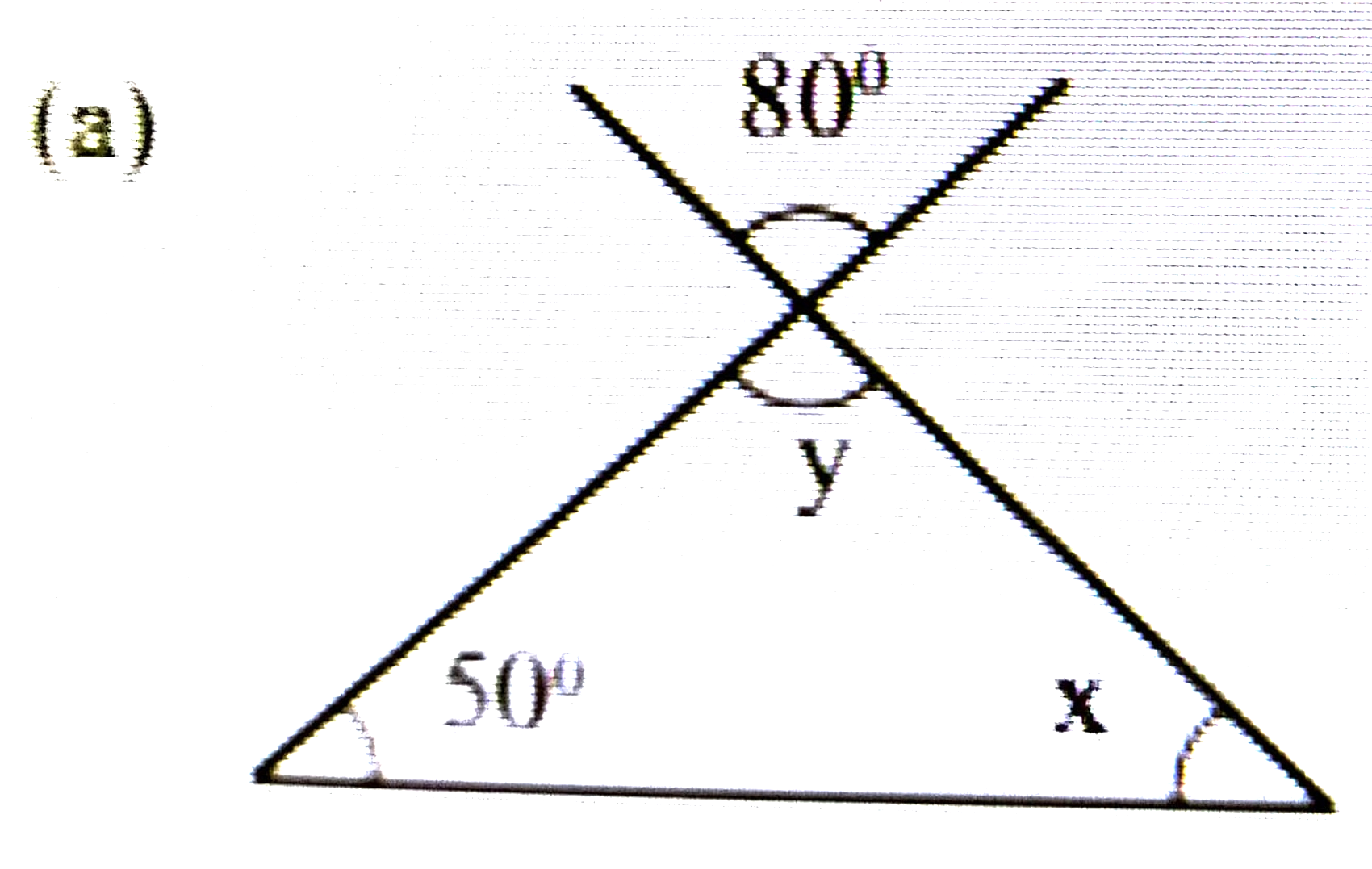
উত্তৰঃ y = 80 [∴ বিপ্রতীপকোণসমান]
∴ x + 50° + y = 180°
⇒ x + 50° + 80° = 180°
⇒ x + 180° – 130° = 50°
উত্তৰঃ y = 60° [বিপ্রতীপকোণসমান]
এতিয়া, x + y + 300 = 180°
⇒ 60° + y + 30° = 180°
⇒ y = 180° – 90° = 90°
(c)

উত্তৰঃ ত্রিভুজ তিনিওটাৰ কোণ সমান
∴ x + x + x = 180° [∴ x = y]
⇒ 3x = 180°
∴ x = 180°/3 = 60°
⇒ y = 60°
3. এটা ত্রিভুজৰ এটা কোণৰ মাপ 60°। বাকী দুটা কোণৰ মাপ তলৰ কোনটো হ’ব?
(a) 50°, 40°
উত্তৰঃ 150° + 40° + 60° = 150° ≠ 180°
(b) 40°, 60°
উত্তৰঃ 40° + 60° + 60° = 160° ≠ 180°
(c) 60°, 70°
উত্তৰঃ 60° + 70° + 60° = 190° ≠ 180°
(d) 50°, 70°
উত্তৰঃ 50° + 70° + 60° = 180°
∴ 50°, 70°
4. চিত্ৰৰ পৰা ∠P নির্ণয় কৰা।
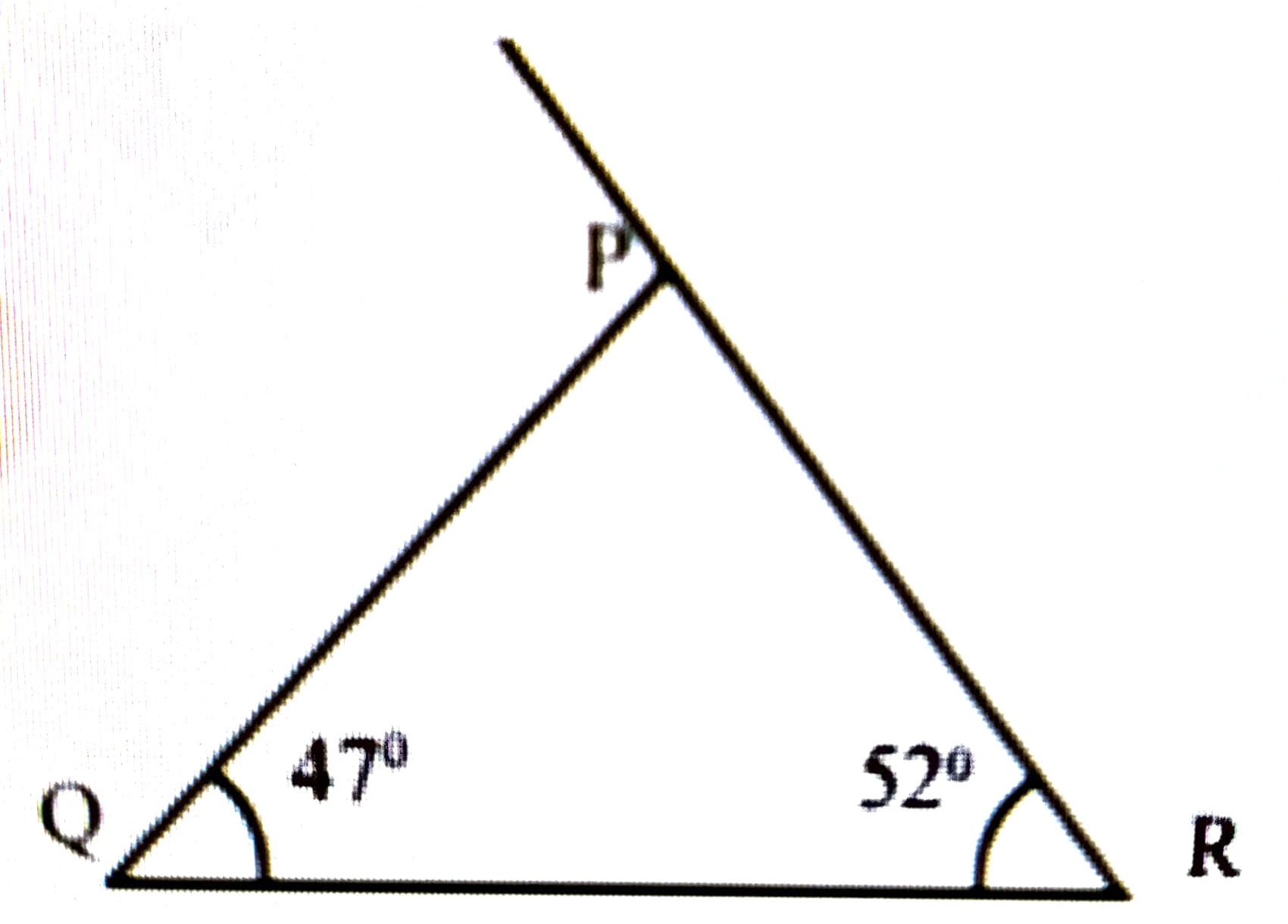
উত্তৰঃ P = 52° + 47° = 99°
5. এটা ত্রিভুজৰ দুটা কোণ 30° আৰু 80°। তৃতীয় কোণটো নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, তৃতীয় কোণাটা x°
∴ x° +30° + 80° = 180°
⇒ x° = 180° – 110° = 70°
6. এটা ত্রিভুজৰ এটা কোণ 80° আৰু বাকী কোণ দুটা পৰস্পৰ সমান। কোণ দুটাৰ জোখ কিমান?
উত্তৰঃ ত্রিভুজৰ এটা কোণ 80°
বাকী কোণ দুটা পৰস্পৰ সমান।
∴ কোণ দটাৰ প্ৰত্যেকৰে জোখ = (180°- 80°)/2 = 100°/2 = 50°
7 . এটা ত্রিভুজৰ কোণ তিনিটাৰ অনুপাত 1:2:1। কোণ তিনিটাৰ জোখ নির্ণয় কৰা।
উত্তৰঃ কোণ তিনিটাৰ অনুপাত 1:2:1
ধৰাহ’ল, কোণ তিনিটা x, 2x আৰু x
∴ x + 2x + x = 180°
⇒ 4x = 180°
∴ x = 45°
∴ কোণ তিনিটা ক্রমে 45°, 2 × 45° = 90° আৰু 45°
৪. এটা ত্রিভুজৰ কোণ তিনিটা ক্রমে (x + 21°), (x – 20°) আৰু (2x – 45°) হ’লে x ৰ মান কিমান?
উত্তৰঃ ত্রিভুজটোৰ কোণ তিনিটা ক্রমে, (x + 21°), (x – 20°) আৰু (2x – 45°)
∴ (x + 21°) + (x – 20°) + (2x – 45°) = 180°
⇒ 4x + (21°- 20°- 45°) = 180°
⇒ 4x = 180° + 44°
⇒ 4x = 224°
∴ x = 224°/4 = 56
9. ত্রিভুজ এটাৰ কোণবোৰৰ অনুপাত 1:2:3। কোণবোৰ মান নির্ণয় কৰা।
উত্তৰঃ ত্রিভুজ এটাৰ কোণবোৰৰ অনুপাত 1:2:3
ধৰাহ’ল, কোণ তিনিটা ক্রমে x, 2x আৰু 3x
∴ x + 2x + 3x = 180°
⇒ 6x = 180°
⇒ x = 180°
⇒ x = 180°/6 = 30°
∴ কোণ তিনিটা ক্রমে, 30°, 2 × 30° = 60° আৰু 3 × 30° = 90°
10. ∆АВС ৰ ∠A + ∠B = 116°, ∠B + ∠C = 126° ত্রিভুজটোৰ অন্তঃকোণবোৰৰ জোখ নির্ণয় কৰা।
উত্তৰঃ ∆ABC ৰ ∠A + ∠B = 116°
∠B + ∠C = 126°
এতিয়া, ∠A + ∠B + ∠C = 180°
⇒ 116° + ∠C = 180°
⇒ ∠C = 180° – 116° = 64°
∴ ∠B = 64° = 126°
⇒ ∠B = 126° – 64° = 62°
∴ ∠A = 116° – ∠B
= 116° – 62° = 54°
11. ∆АВС ৰ 2 ∠A = 3 ∠B = 6 ∠C হ’লে ∠A, ∠B আৰু ∠C উলিওৱা।
উত্তৰঃ ∆ABC ৰ 2 ∠A = 3 ∠B = 6 ∠C
এতিয়া, 3 ∠B = 6 ∠C
⇒ ∠B = 6/3 ∠C = 2 ∠C
2∠A = 6∠C
∴ ∠A = 6/2 ∠C = 3 ∠C
এতিয়া, ∠A + ∠B + ∠C = 180°
⇒ 3 ∠C + ∠A + ∠C = 180°
⇒ 6 ∠C = 180°
⇒ ∠C = 30°
∴ ∠A = 3 × 30° = 90°
∠B = 2 × 30° = 60°
∠C = 30°
12. চিত্রত ∠CAB = 40°, AC = AB আৰু BC = BD
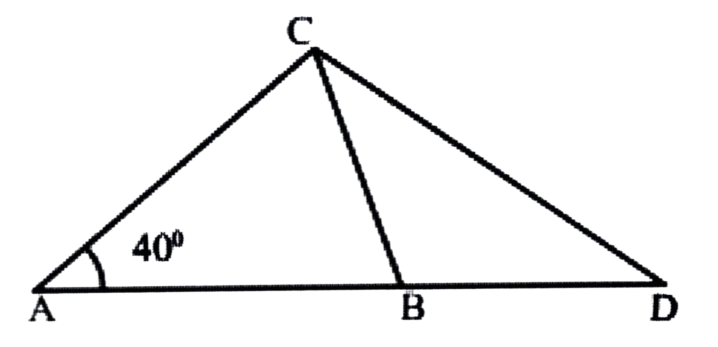
(a) ∠ACB আৰু
(b) ∠CDB মান নির্ণয় কৰা।
উত্তৰঃ চিত্রত ∠CAB = 40°
AC = AB
∴ ∠C = ∠B
এতিয়া, ∠A + ∠B + ∠C = 180°
⇒ 40° + 2 ∠B = 180°
⇒ 2 ∠B = 180° – 40°
∴ ∠B = 140°/2 = 70°
∴ ∠C = 70°
∴ ∠CBD = 40° + 70° = 110°
অৰ্থাৎ, ∠ACB = 70°
আকৌ, BC = BD
∴ ∠BCD = ∠CDB
∴ ∆BCD ৰ পৰা পাওঁ, ∠CBD + ∠BCD + ∠CDB = 180°
⇒ ∠110° + 2 ∠CDB = 180°
⇒ 2180° CDB = 180° – 110°
⇒ ∠CDB = 70°
∴ ∠CDB = 70°/2 = 35°
অনুশীলনী – 6.4 |
|---|
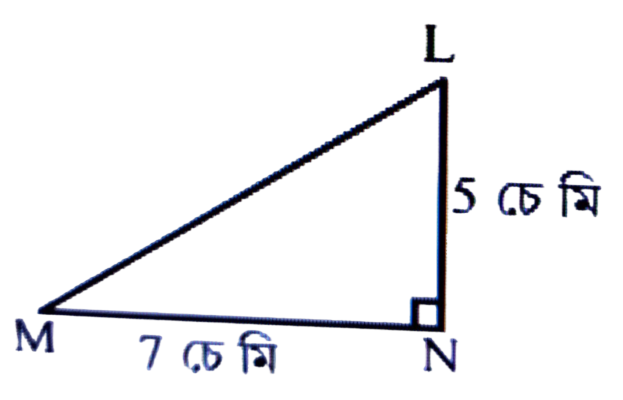
1. চিত্রত AB = 10 চে.মি. BC = 17 চেমি আৰু AD = 8 চেমি. AC নির্ণয় কৰা।
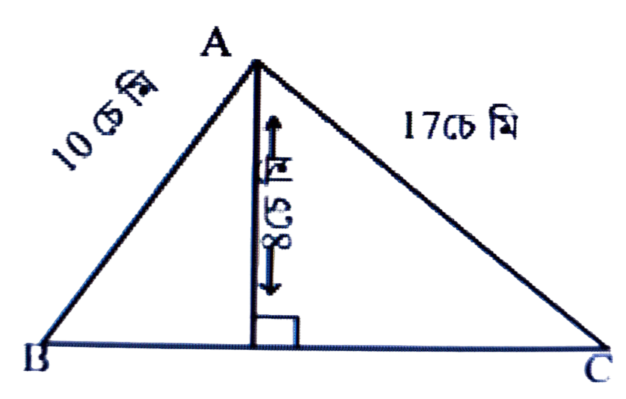
উত্তৰঃ চিত্রত, AB = 10 চে.মি.
BC = 17 চে.মি. আৰু AD = 8 চে.মি.
∴ BD² = AB² – AD²
= 100² – 8² = 100 – 64 = 36
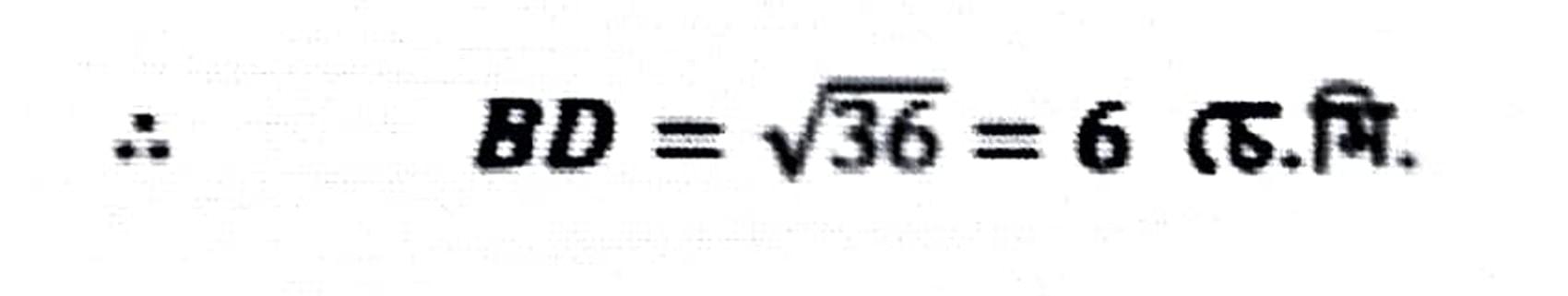
∴ CD = BC – BD = (17 – 6) চে. মি. = 11 চে. মি.
∴ AC² = AD² + CD²
= 8² + 11² = 64 + 121 = 185
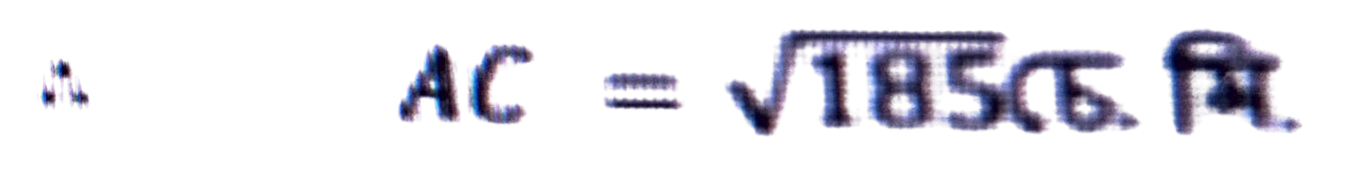
2. এটা ত্রিভুজৰ পৰিসীমা 15 চে.মি.। যদি দুডাল বাহু 5 চে.মি. আৰু 7 চে.মি. জোখৰ হয় তৃতীয় বাহুডালৰ জোখ কিমান?
উত্তৰঃ ধৰাহ’ল, তৃতীয় বাহুডালৰ দীঘ = x চে.মি.
∴ x + 5 + 7 = 15
⇒ x = 15 – 12 – 3
∴ তৃতীয় বাহুটোৰ দীঘ 3 চে.মি.।
3. আয়ত এটাৰ দুডাল সন্নিহিত বাহুৰ জোখ 16 চে.মি. আৰু 12 চে.মি.। কর্ণ দুডালৰ প্রতিডালৰ দীঘ কিমান?
উত্তৰঃ আয়ত এটাৰ কৰ্ণদুডালৰ দীঘ সমান আৰু আয়তৰ এটা কোণ 90°
ধৰাহ’ল, প্রতিডাল কৰ্ণৰ দীঘ x চে.মি.
∴ x² = 16² + 12²
= 256 + 144 = 400
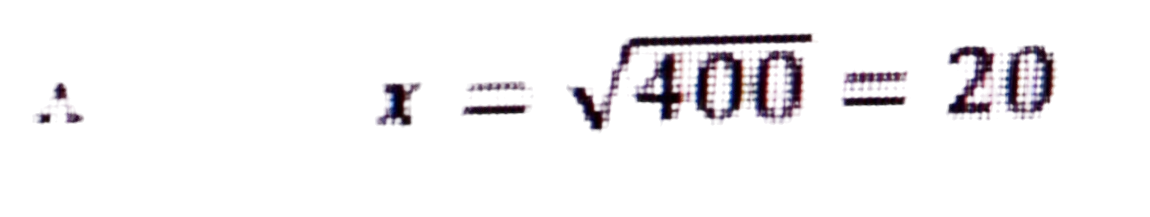
∴ প্রতিডাল কৰ্ণৰ দীঘ = 20 চে.মি.
4. ∆ABC ৰ O এটা বহিঃস্থ বিন্দু। দেখুওৱা যে 2(OA + OB + OC) > AB + BC + CA

উত্তৰঃ ∆ABC ৰ ‘O’ এটা বহিঃস্থ বিন্দু। দেখুৱাব যে-
2(OA + OB + OC) > AB + BC + CA
প্রমাণ: ∆ΟΑΒ ৰ OA + OB > AB ………….. (i)
∆ОАС ৰ OA + OC > AC ………. (ii)
∆ΟΑΒΒC ৰ OB + OC > BC ……….. (iii)
(1), (2) আৰু (3) ৰ পৰা পাওঁ, 2(OA + OB + OC) > AB + BC + CA
5. তলৰ জোখবিশিষ্ট বাহুবোৰে সমকোণী ত্রিভুজ গঠন কৰিবনে?
(a) 5, 12, 13
উত্তৰঃ ধৰা হ’ল, a = 5, b = 12, c = 13
a² = 5² = 25
b² = 12² = 144
c² = 13² = 169
∴ a² + b² = 25 + 144 = 169 = 13² = c²
∴ প্রদত্ত বাহবোৰেৰে এটা সমকোণী ত্রিভুজ পোৱা যাব।
(b) 3, 4, 5
উত্তৰঃ ধৰা হ’ল, a = 3, b = 4, c = 5
a² = 3² = 9
b² = 4² = 16
c² = 5² = 25
∴ a² + b² = 9 + 16 = 25 = 5² = c²
∴ প্রদত্ত বাহুবোৰেৰে এটা সমকোণী ত্রিভুজ পোৱা যাব।
(c) 6, 8, 10
উত্তৰঃ ধৰা হ’ল, a = 6, b = 8, c = 10
এতিয়া, a² = 6² = 36
b² = 8² = 64
c² = 10² = 100
∴ a² + b² = 36 + 64 = 100 = 10² = c²
∴ প্রদত্ত বাহুবোৰেৰে এটা সমকোণী ত্রিভুজ পোৱা যাব।
(d) 6, 7, 8
উত্তৰঃ ধৰা হ’ল, a = 6, b = 7,c = 8
এতিয়া, a² = 6² = 36
b² = 7² = 49
c² = 8² = 64
∴ a² + b² = 36 + 49 = 85 ≠ c²
∴ প্রদত্ত বাহুবোৰেৰে এটা সমকোণী ত্রিভুজ পোৱা নাযাব।
6. তলৰ জোখবোৰ এটা ত্রিভুজৰ বাহু হ’বনে?
(a) 3 চে.মি., 4 চে.মি., 5 চে.মি.
উত্তৰঃ আমি জানো যে, ত্রিভুজৰ দুটা বাহুৰ যোগফল তৃতীয় বাহুতকৈ ডাঙৰ।
এতিয়া, (a) 3 চে.মি. + 4 চে.মি. = 7 চে.মি. > 5 চে.মি.
∴ প্রদত্ত জোখবোৰেৰে এটা ত্রিভুজ পোৱা যাব।
(b) 5 চে.মি, 7 চে.মি., 12 চে.মি.
উত্তৰঃ 5 চে.মি. + 7 চে.মি. = 12 চে.মি.
∴ প্রদত্ত জোখবোৰেৰে এটা ত্রিভুজ পোৱা নাযাব।
(c) 3.4 চে.মি., 2 চে.মি., 5.8 চে.মি.
উত্তৰঃ 3.4 চে.মি. + 2 চে.মি. = 5.4 চে.মি. ≯ 5.8 চে.মি.
∴ প্রদত্ত জোখবোৰেৰে এটা ত্রিভুজ পোৱা নাযাব।
(d) 6 চে.মি., 7 চে.মি., 14 চে.মি.
উত্তৰঃ 6 চে.মি. + 7 চে.মি. = 13 চে.মি. ≯ 14 চে.মি.
∴ প্রদত্ত জোখবোৰেৰে এটা ত্রিভুজ পোৱা নাযাব।
7. ABCD এটা চতুর্ভুজ হ’লে প্রমাণ কৰা যে AB + BC + CD + DA > AC + BD

উত্তৰঃ দিয়া আছে,
ABCD চতুভূজ।
আমি জানো,
ত্ৰিভূজৰ দুটা বাহুৰ জোখবোৰ তৃতীয় বাহুতকৈ ডাঙৰ।
∴ ∆ABC ৰ পৰা
AB + BC > AC → (i)
আকৌ, ∆ABD ৰ পৰা,
AD + AB > BD → (ii)
∆ADC ৰ পৰা,
AD + CD > AC → (iii)
আৰু ∆BDC ৰ পৰা,
BC + CD > BD → (iv)
এতিয়া, (i) + (ii) + (iii) + (iv)
⇒ AB + BC + AD + AB + AD + CD + BC + CD > AC + BD + AC + BD
⇒ 2AB + 2BC + 2AD + 2CD > 2AC + 2BD
⇒ 2(AB + BC + AD + CD) > 2(AC + BD)
∴ AB + BC + AD + CD > AC + BD
অনুশীলনী – 6.5 |
|---|
প্রশ্ন নং 1ৰ পৰা 12 লৈ প্রত্যেক প্ৰশ্নৰ বাবে চাৰিটাকৈ সম্ভাৱ্য উত্তৰ দিয়া আছে। শুদ্ধ উত্তৰটো বাছি উলিওৱা।
1. তলৰ চিত্ৰত x ৰ মান হ’ব–

(a) 40°
(b) 60°
(c) 35°
(d) 180°
উত্তৰঃ (b) 60°
2. x ৰ মান হ’ব–
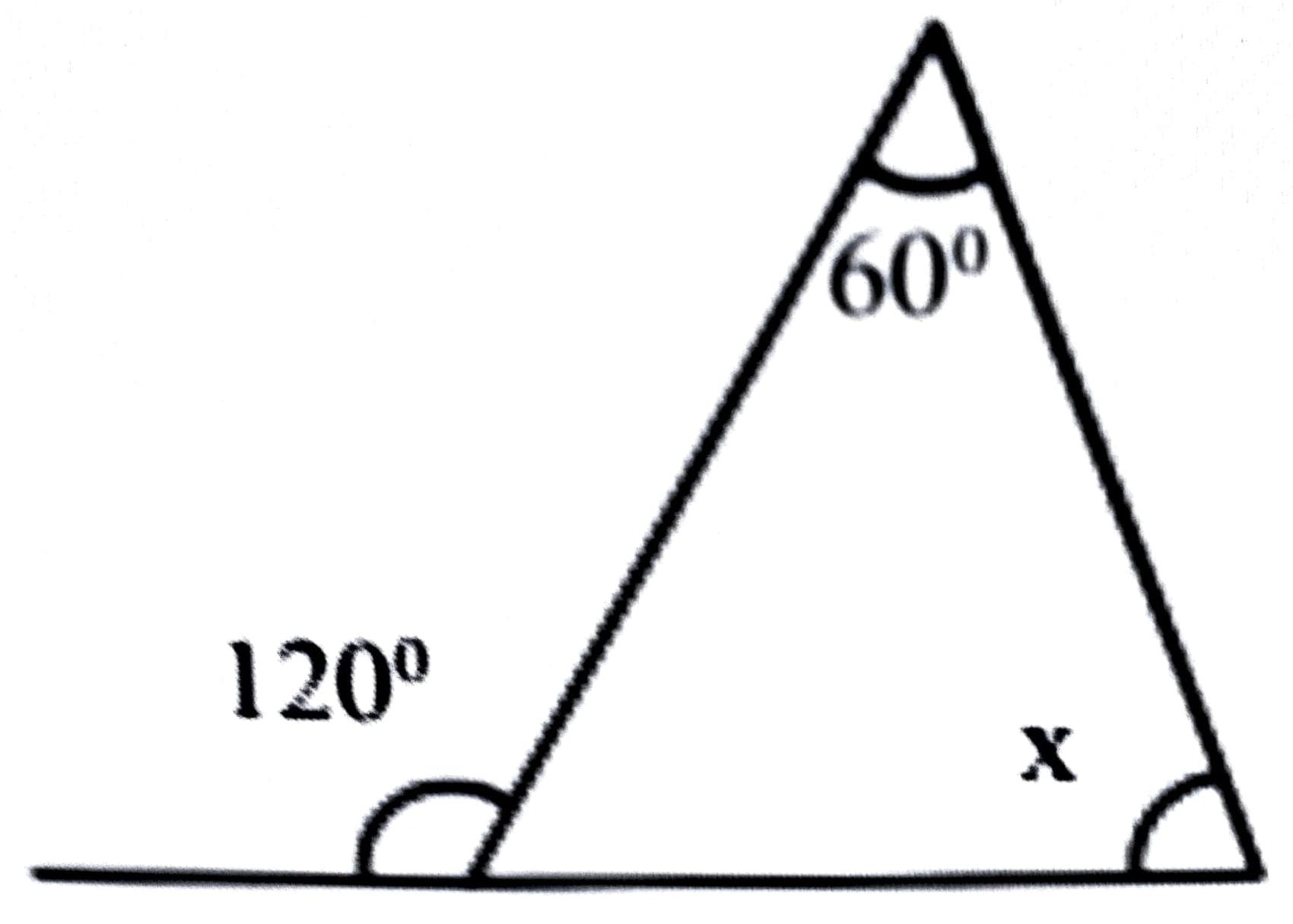
(a) 180°
(b) 55°
(c) 90°
(d) 60°
উত্তৰঃ (d) 60°
3. ΔΑΒC ৰ ∠A = 35°, ∠B = 65° হ’লে ∠C=?
(a) 50°
(b) 80°
(c) 30°
(d) 60°
উত্তৰঃ (b) 80°
4. সমকোণী ত্রিভুজ এটাৰ অতিভুজৰ জোখ 17 চে.মি.। যদি এডাল বাহু 8 চে.মি. জোখৰ হয় তেনেহ’লে আনডালৰ জোখ।
(a) 15 চে.মি.
(b) 12 চে.মি.
(c) 13 চে.মি.
(d) 25 চে.মি.
উত্তৰঃ (a) 15 চে.মি.
5. ΔАВС ৰ ∠A = 72°, ∠B = 63° হ’লে ∠C = ?
(a) 45°
(b) 80°
(c) 30°
(d) 60°
উত্তৰঃ (a) 45°
6. সমকোণী ত্রিভুজ এটাৰ এটা সূক্ষ্মকোণৰ জোখ 36° হ’লে আনটোৰ জোখ কিমান?
(a) 55°
(b) 54°
(c) 51°
(d) 52°
উত্তৰঃ (b) 54°
7. চিত্ৰত x ৰ জোখ নিৰ্ণয় কৰা।
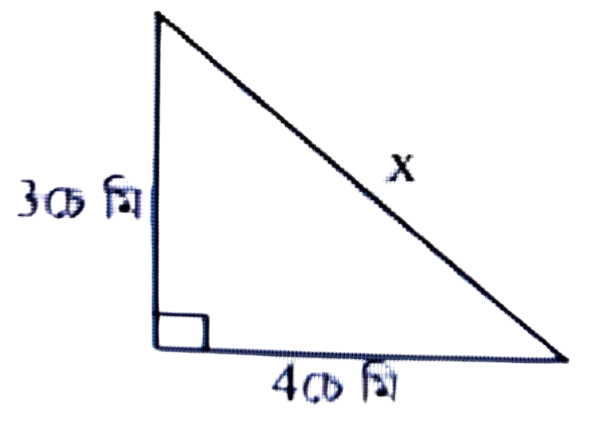
(a) 5 চে.মি.
(b) 7 চে.মি.
(c) 3 চে.মি.
(d) 4 চে.মি.
উত্তৰঃ (a) 5 চে.মি.
৪. চিত্ৰত x ৰ দীঘ কিমান?

(a) 15 চে.মি.
(b) 17 চে.মি.
(c) 13 চে.মি.
(d) 14 চে.মি.
উত্তৰঃ (b) 17 চে.মি.
9. সমকোণী ∆ABC ৰ ∠C = 90°। যদি AC = 5 চে.মি., BC = 12 চে.মি. তেন্তে AB হ’ব।
(a) 7 চে.মি.
(b) 17 চে.মি.
(c) 13 চে.মি.
(d) 14 চে.মি.
উত্তৰঃ (c) 13 চে.মি.
10. ∆PQR ৰ ∠P = 90°, PQ = 3 চে.মি., PR = 4 চে.মি. তেন্তে QR হ’ব।
(a) 7 চে.মি.
(b) 17 চে.মি.
(c) 5 চে.মি.
(d) 13 চে.মি.
উত্তৰঃ (c) 5 চে.মি.
11. চিত্ৰত x ৰ মান হ’ব।
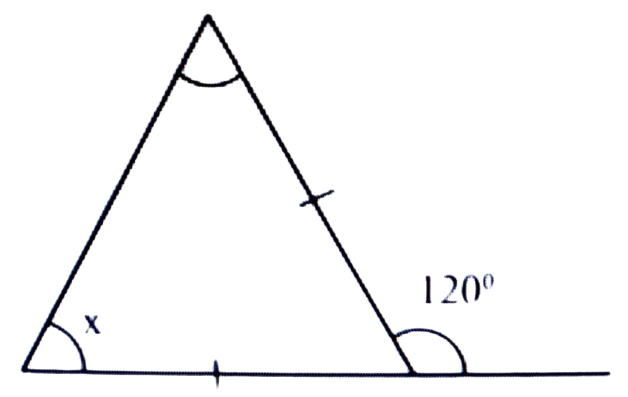
(a) 90°
(b) 60°
(c) 80°
(d) 40°
উত্তৰঃ (b) 60°
12. পাইথাগোৰাছৰ উপপাদ্যটো সিদ্ধ হয় যদিহে ত্রিভুজটো।
(a) স্থূলকোণী।
(b) সমকোণী।
(c) সূক্ষ্মকোণী।
উত্তৰঃ (b) সমকোণী।
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

