SEBA Class 7 Mathematics Chapter 4 – “সৰল সমীকৰণ” solutions
Find SEBA Class 7 Mathematics Chapter 4 – “সৰল সমীকৰণ” (Simple Equations) solutions, designed for Assamese medium students. This chapter explains the concept of equations, variables, and solving methods in a step-by-step approach.
Students will learn about forming equations from word problems, transposition method, balancing equations, and real-life applications of algebraic equations. The chapter also covers how to solve linear equations in one variable using different mathematical operations.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students improve problem-solving skills and prepare effectively for exams.
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীলনী – 4.1 |
|---|
1. তলৰ উক্তিবোৰ সমীকৰণত প্ৰকাশ কৰাঃ
(i) এটা সংখ্যাৰ 6 গুণৰ লগত 5 যোগ কৰিলে 35 পোৱা যাব।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
∴ সমীকৰণটো হ’ব 6x + 5 = 35
(ii) এটা সংখ্যাৰ এক চতুর্থাংশ 9 ৰ সমান।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
∴ x ৰ এক চতুর্থাংশ = x/4
∴ সমীকৰণটো = x/4 = 9
(iii) এটা সংখ্যাৰ 5 গুণ, 20 তকৈ 5 বেছি।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
∴ x ৰ 5 গুণ = 5x
∴ সমীকৰণটো হ’ব 5x – 5 = 20
বা 5 x 20 = 5
(iv) 10 পাবলৈ এটা সংখ্যাৰ 7 গুণৰ লগত 3 যোগ কৰা।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
∴ সমীকৰণটো 7x + 3 = 10
(v) এটা সংখ্যাৰ এক পঞ্চমাংশৰ পৰা 4 বিয়োগ কৰিলে 2 পোৱা যাব।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
সংখ্যাটোৰ এক পঞ্চমাংশ = x/5
∴ সমীকৰণটো = x/5 – 4 = 2
(vi) p ৰ 4 গুণ 20 ৰ সমান।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো p
∴ সমীকৰণ 4p = 20
(vii) এটা সংখ্যাৰ তিনি গুণৰ পৰা 1 বিয়োগ কৰিলে 2 হয়।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
∴ সমীকৰণটো 3x – 1 = 12
(viii) 40 পাবলৈ এটা সংখ্যাক 10 ৰে হৰণ কৰি 10 বিয়োগ কৰা।
উত্তৰঃ ধৰাহ’ল সংখ্যাটো x
∴ সমীকৰণটো x/10 – 10 = 40
2. তলৰ সমীকৰণবোৰ উক্তি আকাৰত লিখাঃ
(i) 3x – 4 = 5
উত্তৰঃ এটা সংখ্যাৰ 3 গুণৰ পৰা 4 বিয়োগ কৰিলে 5 পোৱা যাব।
(ii) m/3 + 6 = 11
উত্তৰঃ m ক 3 ৰে হৰণ কৰিলে হৰণফলৰ লগতে 6 যোগ কৰিলে 11 পোৱা যাব।
(iii) 7p = 42
উত্তৰঃ এটা সংখ্যা 7 গুণ 42 ৰ সমান।
(iv) y/6 = 2
উত্তৰঃ এটা সংখ্যাক 6 ৰে হৰণ কৰিলে 2 পোৱা যাব।
(v) 5x + 7 = 2
উত্তৰঃ এটা সংখ্যাৰ 5 গুণৰ লগত 7 যোগ কৰিলে 2 পোৱা যাব।
(vi) q/2 – 1 = 4
উত্তৰঃ এটা সংখ্যাৰ আধাৰ পৰা 1 বিয়োগ কৰিলে 4 পোৱা যাব।
3. তলৰ উক্তিবোৰৰ পৰা এটাকৈ সমীকৰণ গঠন কৰাঃ
(i) অনুপমা, নিৰুপমা আৰু উপমাৰ বয়সৰ সমষ্টি 22 বছৰ, অনুপমা নিৰুপমাতকৈ 1 বছৰ সৰু, উপমা নিৰুপমাতকৈ 2 বছৰৰ ডাঙৰ। নিৰুপমাৰ বয়সেৰে সমীকৰণ গঠন কৰা।
উত্তৰঃ ধৰা হ’ল নিৰুপমাৰ বয়স x বছৰ
∴ সমীকৰণটো হ’ব 3x + 1 = 22
(ii) অঞ্জনৰ ককাকৰ বয়স 72 বছৰ। ককাকৰ বয়স অঞ্জনৰ বয়সৰ 7 গুণতকৈ 2 বছৰ বেছি।
উত্তৰঃ ধৰা হ’ল অঞ্জনৰ বয়স x বছৰ
∴ সমীকৰণটো হ’ব 7x + 2 = 72
(iii) এটা বৰ্গৰ পৰিসীমা 32 চে.মি.।
উত্তৰঃ ধৰা হ’ল, বৰ্গৰ বাহুৰ দীঘ a একক
∴ সমীকৰণটো হ’ব 4a = 32
(iv) ৰমেনৰ দেউতাকে প্রতি কি.গ্রা 20 টকা দৰত আলু আৰু প্রতি কি.গ্রা 10 টকা দৰত পিয়াজ কিনিলে। তেওঁ আলুৰ পৰিমাণ (কি.গ্রা) তকৈ 1 কি.গ্রা কম পিঁয়াজ কিনাৰ পিছত বেপাৰীক 50 টকা দিলে।
উত্তৰঃ ধৰা হ’ল, আলুৰ পৰিমাণ x কি.গ্রাম
∴ সমীকৰণটো হ’ব 20x + 10(x – 1) = 50
(v) ত্রিভুজৰ দুটা কোণৰ মাপ আটাইতকৈ সৰু কোণটোৰ যথাক্রমে দুগুণ আৰু তিনিগুণ। ত্রিভুজৰ তিনিটা কোণৰ মাপৰ সমষ্টি 180°।
উত্তৰঃ ধৰা হ’ল, আটাইতকৈ সৰু কোণটো x
∴ সমীকৰণটো হ’ব x + 2x + 3x = 180°
4. বন্ধনীৰ ভিতৰত থকা মানটোত সমীকৰণটো সিদ্ধ হয় নে নহয় কোৱা।
(i) x + 5 = 0, (x = -5)
উত্তৰঃ x + 5 = 0, সমীকৰণটোত x = -5 বহুৱালে পাম
-5 + 5 = 0
∴ x = -5 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
(ii) 2x – 8 = 7, (x = 4)
উত্তৰঃ 2x – 8 = 7, সমীকৰণটোত x = 4 বহুৱালে পাম
2 x 4 – 8 = 0
∴ x = 4 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
(iii) x/3 + 6 = 7, (x = 3)
উত্তৰঃ x/3 + 6 = 7, সমীকৰণটোত x = 3 বহুৱালে পাম
3/3 + 6 = 1 + 6 = 7
∴ x = 3 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
(iv) x/7 – 2 = 0, (x = 7)
উত্তৰঃ x/7 – 2 = 0, সমীকৰণটোত x = 7 বহুৱালে পাম
7/7 – 62 = 1 – 2 = -1
∴ x = 7 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
(v) 5x = 35, (x = 7)
উত্তৰঃ 5x = 35, সমীকৰণটোত x = 7 বহুৱালে পাম
5 × 7 = 35,
∴ x = 7 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
(vi) 4x + 8 = 4, (x = -1)
উত্তৰঃ 4x + 8 = 4, সমীকৰণটোত x = -1 বহুৱালে পাম
4 × (-1) + 8 = -4 + 8 = 4
∴ x = -1 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
(vii) 7x + 2 = 9, (x = 2)
উত্তৰঃ 7x + 2 = 9,
7 × 2 = 14 + 2 = 16
∴ x = 2 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
(viii) 2x = 16, (x = 8)
উত্তৰঃ 2x = 16, সমীকৰণটোত x = ৪ বহুৱালে পাম
2 × 8 = 16
∴ x = 8 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
(ix) x/5 = 20, (x = 100)
উত্তৰঃ x/5 = 20, সমীকৰণটোত x = 8 বহুৱালে পাম
100/5 = 20
∴ x = 100 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
(x) x/8 + 4 = 9, (x = 1)
উত্তৰঃ x/8 + 4 = 9, সমীকৰণটোত x = 1 বহুৱালে পাম
1/8 + 4 = (1 + 32)/8 = 33/8
∴ x = 1 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
5. বন্ধনীৰ ভিতৰত থকা মানটো সমীকৰণটোৰ এটা সমাধান হয় নে নহয় পৰীক্ষা কৰা।
(i) 4x + 3 = 7, (x = 1)
উত্তৰঃ 4x + 3 = 7 সমীকৰণটোত x = 1 বহুৱালে পাম
4 × 1 + 3
∴ x = 1 সমীকৰণটোৰ এটা সমাধান।
(ii) 2x/3 + 5 = 7, (x = 3)
উত্তৰঃ 2x/3 + 5 = 7 সমীকৰণটোত x = 3 বহুৱালে পাম
(2 × 3)/3 + 5 = 6/3 + 5 = 2 + 5 = 7
∴ x = 3 সমীকৰণটোৰ এটা সমাধান।
(iii) x – 4 = 1, (x = 3)
উত্তৰঃ x – 4 সমীকৰণটোত x = 3 বহুৱালে পাম
x × 4 = -1
∴ x = 3 সমীকৰণটোৰ এটা সমাধান নহয়।
(iv) 6x = 18, (x = 2)
উত্তৰঃ 6x = 18 সমীকৰণটোত x = 2 বহুৱালে পাম
6x × 2 = 12
∴ x = 2 সমীকৰণটোৰ সমাধান নহয়।
(v) 5x – 1 = 7, (x = 2)
উত্তৰঃ 5x – 1 = 7, সমীকৰণটোত x = 2 বহুৱালে পাম
5 × 2 – 1 = 10 – 1 = 9
∴ x = 2 সমীকৰণটোৰ সমাধান নহয়।
(vi) x + 9 = 13, (x = 4)
উত্তৰঃ x + 9 = 13, সমীকৰণটোত x = 4 বহুৱালে পাম
4 + 9 = 13
∴ x = 2 সমীকৰণটোৰ এটা সমাধান।
(vii) 5x – 7 = 8, (x = 3)
উত্তৰঃ 5x – 7 = 8, সমীকৰণটোত x = 3 বহুৱালে পাম
5 × 3 – 7 = 15 – 7 = 8
∴ x = 9 সমীকৰণটোৰ এটা সমাধান।
(viii) y/3 + 5 = 8, (y = 9)
উত্তৰঃ y/3 + 5 = 8, সমীকৰণটোত y = 9 বহুৱালে পাম
9/3 + 5 = 3 + 5 = 8
∴ x = 9 সমীকৰণটোৰ এটা সমাধান।
(ix) p/5 + 4 = 5, (p = 1)
উত্তৰঃ p/5 + 4 = 5, সমীকৰণটোত P = 1 বহুৱালে পাম
1/5 + 4 = (1 + 20)/5 = 21/5
∴ P = 1 সমীকৰণটোৰ সমাধান নহয়।
(x) x/7 = 6, (x = 42)
উত্তৰঃ x/7 = 6, সমীকৰণটোত x = 42 বহুৱালে পাম
42/7 = 6
∴ x = 42 সমীকৰণটোৰ এটা সমাধান।
6. x ৰ ঠাইত বিভিন্ন মান বহুৱাই সমাধানৰ চেষ্টা কৰা। (প্ৰচেষ্টা আৰু ভুল পদ্ধতি)
(i) 2x + 5 = 11
উত্তৰঃ 2x + 5 = 11
x = 1 বহুৱালে 2 × 1 + 5 = 2 + 5 = 7
∴ x = 1 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
x = 2 বহুৱালে 2 × 2 + 5 = 4 + 5 = 9
∴ x = 2 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
x = 3 বহুৱালে 2 × 3 + 5 = 6 + 5 = 11
∴ x = 3 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
∴ সমীকৰণটোৰ সমাধান x = 3
(ii) x/5 + 5 = 7
উত্তৰঃ x/5 + 5 = 7
x = 1 বহুৱালে 1/5 + 5 = (1 + 25)/5 = 26/5
∴ x = 1 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
x = 2 বহুৱালে 2/5 + 5 = (2 + 25)/5 = 27/5
∴ x = 2 ৰ বাবে সমীকৰণটো সিদ্ধ নহয়।
x = 10 ৰ বাবে, 10/5 + 5 = 2 + 5 = 7
∴ x = 10 ৰ বাবে সমীকৰণটো সিদ্ধ হয়।
∴ সমীকৰণটোৰ সমাধান x = 10
(iii) 7x – 4 = 24
উত্তৰঃ 7x – 4 = 24
x = 1 বহুৱালে 7 × 1 – 4 ≠ 24
∴ সমীকৰণটো সিদ্ধ নহয়।
x = 2 বহুৱালে 7 × 2 – 4 ≠ 24
∴ সমীকৰণটো সিদ্ধ নহয়।
x = 3 বহুৱালে 7 × 3 – 4 ≠ 24
∴ সমীকৰণটো সিদ্ধ নহয়।
x = 4 বহুৱালে 7 × 4 – 4 ≠ 28 – 4 = 24
∴ সমীকৰণটো সিদ্ধ নহয়।
∴ x = 4 সমীকৰণটোৰ সমাধান।
অনুশীলনী – 4.2 |
|---|
1. চলকটো পৃথক কৰোঁতে ব্যৱহাৰ কৰা প্ৰথম স্তৰটো লিখা আৰু সমীকৰণটো সমাধান কৰা।
(i) x + 5 = 12
উত্তৰঃ x + 5 = 12
= x + 5 – 5 = 12 – 5
= 7
(ii) x – 7 = 0
উত্তৰঃ x – 7 = 0
= (x – 7) + 7 = 0 + 7
= 7
(iii) y – 3 = 6
উত্তৰঃ y – 3 = 6
= y – 3 + 3 = 6 + 3
= 9
(iv) z + 6 = 5
উত্তৰঃ z + 6 = 5
= z + 6 – 6 = 5 – 6
= -1
(v) 3x = 42
উত্তৰঃ 3x = 42
= 3x/3 = 42/3
= 14
(vi) x/5 = 6
উত্তৰঃ x/5 = 6
= 5 × x/5 = 5 × 6
= 30
(vii) 12x = -36
উত্তৰঃ 12x = -36
= 12x/12 = -36/12
= -3
(viii) x/4 = 3/2
উত্তৰঃ x/4 = 3/2
= x/4 × 4 = 3/4 × 4
= 6
(ix) 7x = 35
উত্তৰঃ 7x = 35
= 7x/7 = 35/7
= 5
(x) p/4 = 3
উত্তৰঃ p/4 = 3
= p/4 × 4 = 3 × 4
= 12
2. চলকটো পৃথক কৰিবলৈ ব্যৱহাৰ কৰিবলগীয়া স্তৰবোৰ লিখা আৰু সমীকৰণটো সমাধান কৰা।
(i) 4x + 5 = 45
(ii) 3x – 7 = 11
(iii) 2x/3 + 5 = 7
(iv) 4y/3 -7 = 5
উত্তৰঃ
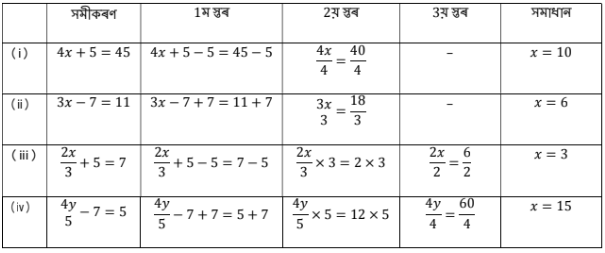
3. তলৰ সমীকৰণবোৰ সমাধান কৰা।
(i) 4x = 64
উত্তৰঃ 4x = 64
⇒ 4x/4 = 64/4
⇒ x = 16
∴ x = 16
(ii) 4x + 7 = 15
উত্তৰঃ 4x + 7 = 15
⇒ 4x + 7 – 7 = 15 – 17
⇒ 4x = 8
⇒ 4x/4 = 8/4
∴ x = 2
(iii) y/4 = 6
উত্তৰঃ y/4 = 6
⇒ 4 × y/4 = 4 × 6
⇒ y = 24
∴ y = 24
(iv) 3y = 60
উত্তৰঃ 3y = 60
⇒ 3y/3 = 60/3
⇒ y = 20
(v) 6p + 7 = 37
উত্তৰঃ 6p + 7 = 37
⇒ 6p + 7 – 7 = 37 – 7
⇒ 6p = 30
⇒ 6p/6 = 30/6
⇒ p = 5
(vi) 7p – 9 = 5
উত্তৰঃ 7p – 9 = 5
⇒ 7p – 9 + 9 = 5 + 9
⇒ 7p = 14
⇒ 7p/7 = 14/7
⇒ p = 2
∴ p = 2
(vii) 5x – 7 = 8
উত্তৰঃ 5x – 7 = 8
⇒ 5x – 7 + 7 = 8 + 7
⇒ 5x = 15
⇒ 5x/5 = 15/5
⇒ x = 3
∴ x = 3
(viii) x/5 + 2 = 3
উত্তৰঃ x/5 + 2 = 3
⇒ x/5 + 2 – 2 = 3 – 2
⇒ x/5 = 1
⇒ x = 5
∴ x = 5
(ix) q/3 – 1 = 2
উত্তৰঃ q/3 – 1 = 2
⇒ q/3 – 1 + 1 = 2 + 1
⇒ q/3 = 3
⇒ 3 × q/3 = 3 × 3
⇒ q = 9
∴ q = 9
(x) 3x + 11 = 50
উত্তৰঃ 3x + 11 = 50
⇒ 3x + 11 – 11 = 50 – 11
⇒ 3x = 39
⇒ 3x/3 = 39/3
⇒ x = 13
∴ x = 13
(xi) 4x + 10 = 26
উত্তৰঃ 4x + 10 = 26
⇒ 4x + 10 – 10 = 26 – 10
⇒ 4x = 16
⇒ 4x/4 = 16/4
⇒ x = 4
∴ x = 4
(xii) x/3 + 4 = 6
উত্তৰঃ x/3 + 4 = 6
⇒ x/3 + 4 – 4 = 6 – 4
⇒ x/3 = 2
⇒ 3 × x/3 = 3 × 2
⇒ x = 6
∴ x = 6
(xiii) p/3 + 5 = 12
উত্তৰঃ p/3 + 5 = 12
⇒ p/3 + 5 = 12
⇒ p/3 + 5 – 5 = 12 – 5
⇒ p/3 = 7
⇒ 3 × p/3 = 3 × 7
⇒ p = 21
∴ p = 21
(xiv) q/2 + 4 = 7
উত্তৰঃ q/2 + 4 = 7
⇒ q/2 + 4 = 7
⇒ q/2 = 3
⇒ 2 × q/2 = 2 × 3
⇒ q = 6
∴ q = 6
(xv) 2(x + 3) = x + 7
উত্তৰঃ 2(x + 3) = x + 7
⇒ 2x + 6 = x + 7
⇒ 2x – x + 6 – 6 = x – x + 7 – 6
⇒ x = 1
∴ x = 1
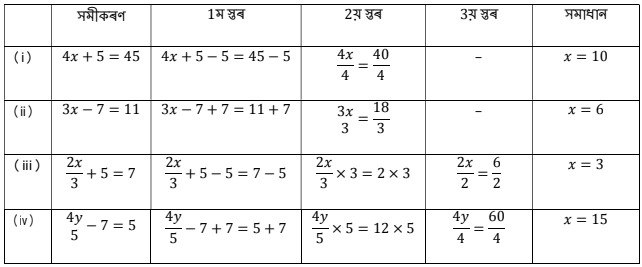
প্ৰশ্ন 3. চলকটো পৃথক কৰিবলৈ ব্যৱহাৰ কৰিবলগীয়া স্তৰবোৰ লিখা আৰু সমীকৰণটো সমাধান কৰা।
(i) 4x + 5 = 45
(ii) 3x – 7 = 11
(iii) 2x/3 + 5 = 7
(iv) 4x/3 – 7 = 5
উত্তৰঃ
অনুশীলনী – 4.3 |
|---|
1. তলত দিয়া সংখ্যাবোৰৰ বাবে সমীকৰণ গঠন কৰা আৰু সমীকৰণ সমাধান কৰি সংখ্যাবোৰ নিৰ্ণয় কৰা।
(i) এটা সংখ্যাৰ 5 গুণৰ পৰা 7 বিয়োগ কৰিলে বিয়োগফল 8 হয়।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, 5x – 7 = 8
⇒ 5x – 7 + 7 = 8 + 7
⇒ 5x = 15
⇒ 5x/5 = 15/5
⇒ x = 3
∴ x = 3
(ii) এটা সংখ্যাৰ এক তৃতীয়াংশ 5তকৈ 2 বেছি।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, x/3 – 5 = 2
⇒ x/3 – 5 + 5 = 2 + 5
⇒ x/3 = 7
⇒ 3x × x/3 = 3 x 7
⇒ x = 21
∴ নির্ণেয় সংখ্যাটো 21
(iii) 10 পাবলৈ এটা সংখ্যাৰ 3 গুণৰ লগত 4 যোগ কৰা।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, 3x + 4 = 10
⇒ 3x + 4 – 4 = 10 – 4
⇒ 3x = 6
⇒ 3x/3 = 6/3
⇒ x = 2
∴ নির্ণেয় সংখ্যাটো 2
(iv) জহিৰুলে এটা সংখ্যাৰ লগত 6 যোগ কৰি, যোগফলক 3 ৰে হৰণ কৰিলে 4 পায়।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, x + 6/3 = 4
⇒ 3 × (x + 6)/3 = 4 × 3
⇒ x + 6 = 12
⇒ x + 6 – 6 = 12 – 6
⇒ x = 6
∴ সংখ্যাটো 6
(v) এটা সংখ্যাৰ দুই-তৃতীয়াংশৰ পৰা 4 বিয়োগ কৰিলে 7 পোৱা যায়।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, x × 2/3 – 4 = 7
⇒ 2x/3 -4 + 4 = 7 + 4
⇒ 2x/3 = 11
⇒ 3 × 2x/3 = 3 × 11
⇒ 2x = 33
⇒ 2x/2 = 33/2
⇒ x = 33/2
∴ নির্ণেয় সংখ্যাটো 33/2
(vi) এটা সংখ্যাৰ 6 গুণ 24 ৰ সমান।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, 6x = 24
⇒ 6x/6 = 24/6
⇒ x = 4
∴ নির্ণেয় সংখ্যাটো 4
(vii) এটা সংখ্যাৰ এক-চতুর্থাংশৰ লগত 5 যোগ কৰিলে 6 পোৱা যায়।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, x × 1/4 + 5 = 6
⇒ x/4 + 5 – 5 = 6 – 5
⇒ x/4 = 1
⇒ 4 × x/4 = 4 × 1
⇒ x = 4
∴ নির্ণেয় সংখ্যাটো 4
(viii) এটা সংখ্যাৰ তিনি-চতুর্থাংশ 12 ৰ সমান।
উত্তৰঃ ধৰা হ’ল সংখ্যাটো x
প্রশ্নমতে, x × 3/4 = 12
⇒ 3x/4 = 12
⇒ 4 × 3x/4 = 4 × 12
⇒ 3x = 48
⇒ 3x/3 = 48/3
⇒ x = 16
∴ সংখ্যাটো 16
2. অমল, ৰমেন আৰু অনুপৰ পকেটত থকা মাৰ্বলৰ সংখ্যা এনে ধৰণৰ–ৰমেনৰ দুয়ো পকেটত মিলি থকা মার্বল অমলৰ পকেটত থকা মাৰ্ললৰ দুগুণ। অনুপৰ পকেটত থকা মাৰ্বলৰ সংখ্যা 11। তেওঁলোকৰ তিনিওজনৰ লগত থকা মাৰ্বলৰ সংখ্যা 50 টা হ’লে, ৰমেন আৰু অনুপৰ লগত থকা মাৰ্বলৰ সংখ্যা কিমান?
উত্তৰঃ ধৰাহ’ল, অমলৰ পকেটত থকা মাৰ্বলৰ সংখ্যা x
∴ ৰমেনৰ পকেটত থকা মাৰ্বলৰ সংখ্যা 2x
প্রশ্নমতে, x + 2x + 11 = 50
⇒ 3x + 11 – 11 = 50 – 11
⇒ 3x = 39
⇒ 3x/3 = 39/3
∴ x = 13
∴ অমলৰ পকেটত থকা মাৰ্বলৰ সংখ্যা = 13
ৰমেনৰ পকেটত থকা মাৰ্বলৰ সংখ্যা = 2 × 12 = 26
3. এটা ভগ্নাংশৰ হৰ লবতকৈ 4 বেছি। যদি ল’ব আৰু হৰৰ সৈতে 1 যোগ কৰা হয় তেন্তে ভগ্নাংশটোৰ মান 1/2 হয়। ভগ্নাংশটো উলিওৱা।
উত্তৰঃ ধৰাহ’ল তগ্নাংশটো x
∴ ভগ্নাংশটোৰ হৰ x + 4
প্রশ্নমতে, x + 1/(x + 4) + 1 = 1/2
⇒ (x + 1)/(x + 5) = 1/2
⇒ 2(x + 1) = x + 5
⇒ 2x + 2 = x + 5
⇒ 2x – x + 2 – 2 = x – x + 5 – 2
⇒ x = 3
∴ নির্ণেয় ভগ্নাংশটো = x/x + 4 = 3/3+4 = 3/7
4. এটি আয়তৰ দৈর্ঘ্য, প্রস্থতকৈ 5 চে.মি. বেছি। আয়তটোৰ পৰিসীমা 26 চে.মি. হ’লে আয়তটোৰ কালি উলিওৱা।
উত্তৰঃ ধৰা হ’ল, আয়তটোৰ x চে.মি.
∴ আয়তটোৰ দৈর্ঘ্য (x + 5) চে.মি.
প্রশ্নমতে, 2 (দীঘ + প্রস্থ) = 26
⇒ 2{(x + 5) + x} = 26
⇒ x + 5 = 13 (2 ৰে দুয়োেপক্ষক হৰণ কৰি)
⇒ 2x + 5 – 5 = 13 – 5
⇒ 2x = 8
⇒ 2x/2 = 8/2
⇒ x = 4
∴ আয়তটোৰ প্ৰস্থ = 4 চে.মি.
আয়তটোৰ দৈর্ঘ্য = (4 + 5) = 9 চে.মি.
5. আৰিফুলৰ মাকৰ বয়স, আৰিফুলৰ ভণ্টী ৰেহানাৰ বয়সৰ 4 গুণ। ৰেহানা আৰিফুলতকৈ 4 বছৰৰ সৰু। ৰেহানাৰ মাকৰ বয়স 32 বছৰ হ’লে আৰিফুল আৰু ৰেহানাৰ বয়স কিমান?
উত্তৰঃ ধৰাহ’ল আৰিফুলৰ বয়স x বছৰ
∴ ৰেহানাৰ বয়স (x – 4) বছৰ
আৰিফুলৰ মাকৰ বয়স = 32 বছৰ
প্রশ্নমতে, 4x(x – 4) = 32
⇒ 4x(x – 4)/4 = 32/4
⇒ x – 4 = 8
⇒ x – 4 + 4 = 8 + 4
⇒ x = 12
∴ আৰিফুলৰ বয়স = 12 বছৰ
ৰেহানাৰ বয়স = (12 – 4) = 8 বছৰ।
6. অনুপম, ৰাহুল আৰু জাহিৰুলৰ বয়সৰ সমষ্টি 22 বছৰ। অনুপম ৰাহুলতকৈ 1 বছৰৰ সৰু। জাহিৰুল ৰাহুলতকৈ 2 বছৰৰ ডাঙৰ হ’লে তেওঁলোকৰ বয়স নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, ৰাহুলৰ বয়স x বছৰ
∴ অনুপমৰ বয়স (x – 1) বছৰ
আৰু জাহিৰুলৰ বয়স (x + 2) বছৰ
প্রশ্নমতে, x + (x – 1) + (x + 2) = 22
⇒ x + x – 1 + x2 = 22
⇒ 3x + 1 = 22
⇒ 3x + 1 – 1 = 22 – 1
⇒ 3x = 21
⇒ 3x/3 = 21/3
⇒ x = 7
∴ ৰাহুলৰ বয়স = 7 বছৰ।
অনুপমৰ = (7 – 1) = 6 বছৰ।
জাহিৰুলৰ বয়স = (7 + 2) = 9 বছৰ।
7. অঞ্জনৰ ককাকৰ বয়স অঞ্জনৰ বয়সৰ 7 গুণতকৈ 2 বছৰ বেছি। অঞ্জনৰ ককাকৰ বয়স 72 বছৰ হ’লে অঞ্জনৰ বয়স নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল অঞ্জনৰ বয়স = x বছৰ
∴ অঞ্জনৰ ককাকৰ বয়স = (7x + 2) বছৰ
প্রশ্নমতে, (7x + 2) = 72
⇒ 7x + 2 – 2 = 72 – 2
⇒ 7x = 70
⇒ 7x/7 = 70/7
⇒ x = 10
∴ অঞ্জনৰ বয়স = 10 বছৰ।
৪. ৰবীন, নৰেন, শ্রেয়া, অনুভৱ, ইৰফান আৰু পাৰুমাই গণিতৰ পৰীক্ষাত পোৱা নম্বৰ এনে ধৰণৰ– শ্রেয়াই পোৱা নম্বৰ নৰেনৰ দুগুণ, অনুভৱে শ্রেয়াতকৈ 5 নম্বৰ কম পাইছে, ইৰফান আৰু নৰেনৰ নম্বৰৰ যোগফল 105, ৰবীনে পাৰুমাতকৈ 5 নম্বৰ কম পাইছে আৰু পাৰুমাই ইৰফানতকৈ 15 নম্বৰ বেছি পাইছে। তেওঁলোকে পোৱা নম্বৰৰ সমষ্টি 435 হ’লে প্রতিজনে পোৱা নম্বৰ নিৰ্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, নৰেনৰ গণিতৰ নম্বৰ x
∴ শ্ৰেয়াৰ গণিতৰ নম্বৰ 2x
অনুভৱৰ গণিতৰ নম্বৰ 2x – 5
ইৰফানৰ আৰু নৰেনৰ গণিতৰ নম্বৰ 105
∴ ইৰফানৰ গণিতৰ নম্বৰ 105 – x
পাৰুমাইৰ গণিতৰ নম্বৰ = 105 – x + 15 = 120 – x
ৰবীণৰ গণিতৰ নম্বৰ = 120 – x – 15 = 115 – x
প্ৰশ্নমতে, x + 2x + 2x – 5 + 105 – x120 – x + 115 – x = 435
⇒ 5x – 3x + 335 = 435
⇒ 2x = 435 – 335
⇒ 2x = 100
⇒ x = 50
∴ নৰেণৰ নম্বৰ = 50
শ্ৰেয়াৰ নম্বৰ = x50 = 100
ইৰফানৰ নম্বৰ = 105 – 50 = 55
ৰবীণৰ নম্বৰ = 115 – 50 = 65
অনুভৱৰ নম্বৰ = 100 – 5 = 95
পাৰুমাৰ নম্বৰ = 120 – 50 = 70
9. তিনিটা ক্রমিক অযুগ্ম সংখ্যাৰ যোগফল 75 হ’লে, সংখ্যা তিনিটা নিৰ্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, ক্রমিক অযুগ্ম সংখ্যা তিনিটা = x + x + 2, {(x + 2) + 2}
প্রশ্নমতে, x + x + 2 + x + 4 = 75
⇒ 3x + 6 = 75
⇒ 3x + 6 – 6 = 75 – 6
⇒ 3x = 69
⇒ 3x/3 = 69/3
∴ x = 23
∴ সংখ্যা তিনিটা 23, 25, 27
10. দুটা ক্রমিক যুগ্ম সংখ্যাৰ যোগফল 38 হ’লে সংখ্যা দুটা নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল ক্রমিক যুগ্ম সংখ্যা দুটা x, x + 2
প্রশ্নমতে, x + x + 2 = 38
⇒ 2x + 2 = 38
⇒ 2x + 2 – 2 – 38 – 2
⇒ 2x = 36
⇒ 2x/2 = 36/2
⇒ x = 18
∴ সংখ্যা দুটা 18,18 + 2 = 20
11. দুই অংকীয়া সংখ্যা এটাৰ দহকৰ ঘৰৰ অংকটো এককৰ ঘৰৰ অংকৰ 3 গুণ। সংখ্যাটোৰ অংক দুটাৰ স্থান সালসলনি কৰি পোৱা নতুন সংখ্যা আৰু মূল সংখ্যাটোৰ সমষ্টি ৪৪ হ’লে, মূল সংখ্যাটো নিৰ্ণয় কৰা।
উত্তৰঃ এককৰ ঘৰৰ অংকটো x
∴ দহকৰ স্থানৰ অংকটো 3x
∴ সংখ্যাটো = 10 × 3x + x = 31x
অংক দুটাই স্থান সালসলনি কৰি পোৱা সংখ্যাটো হ’ব–
= 10 × x + 3x = 13x
প্রশ্নমতে, 13x + 31x = 88
⇒ 44x = 88
⇒ 44x/44 = 88/44
⇒ x = 2
∴ সংখ্যাটো = 31 x 2 = 62
12. তিনিটা ক্রমিক সংখ্যাৰ যোগফল 48 হ’লে সংখ্যা তিনিটা নিৰ্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, সংখ্যা তিনিটা ক্রমে, x, x + 1, x + 2
প্রশ্নমতে, x + (x + 1) + (x + 2) = 48
⇒ 3x + 3 = 48
⇒ 3x + 3 – 3 = 48 – 3
⇒ 3x = 45
⇒ 3x/3 = 45/3
⇒ x = 15
∴ সংখ্যা তিনিটা ক্রমে, 15,16,17
13. দুটা সংখ্যাৰ যোগফল 40। এটা সংখ্যা আনটোতকৈ 10 বেছি, সংখ্যা দুটা নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, এটা সংখ্যা x
আনটো সংখ্যা x + 10
প্রশ্নমতে, x + x + 10 = 40
⇒ 2x + 10 = 40
⇒ 2x + 10 – 10 = 40 – 10
⇒ 2x = 30
⇒ 2x/2 = 30/2
⇒ x = 15
∴ এটা সংখ্যা = 15
আনটো সংখ্যা = 15 + 10 = 25
14. দুটা সংখ্যাৰ অনুপাত ৪:3। সংখ্যা দুটাৰ বিয়োগফল 60 হ’লে সংখ্যা দুটা নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, সংখ্যা দুটা ক্রমে, ৪x আৰু 3x
প্রশ্নমতে, 8x – 3x = 60
⇒ 5x = 60
⇒ 5x/5 = 60/5
⇒ x = 12
∴ সংখ্যা দুটা ক্রমে, 8x = 8 × 12 = 96
⇒ 3x = 3 × 12 = 36
15. এটা আয়তৰ দীঘ, প্ৰস্থৰ 2 গুণ। আয়তটোৰ পৰিসীমা 72 হ’লে আয়তটোৰ দীঘ আৰু প্রস্থ উলিওৱা।
উত্তৰঃ ধৰাহ’ল, আয়তটোৰ প্ৰস্থ = x একক
∴ আয়তটোৰ দীঘ = 2x একক
প্রশ্নমতে, 2(2x + x) = 72
⇒ 3x = 72/2
⇒ 3x = 36
⇒ 3x/3 = 36/3
⇒ x = 12
∴ আয়তটোৰ প্ৰস্থ = 12 একক
আয়তটোৰ দীঘ = 2 × 12 একক = 24 একক।
16. অজয়, বিজয়তকৈ 5 বছৰৰ সৰু। 4 বছৰ পিছত বিজয়ৰ বয়স অজয়ৰ দুগুণ হ’লে, তেওঁলোকৰ বর্তমান বয়স কিমান?
উত্তৰঃ ধৰাহ’ল, বিজয় বয়স = x বছৰ
∴ অজয়ৰ বয়স = (x – 4) বছৰ
4 বছৰ পিছত বিজয়ৰ বয়স হ’ব = (x + 4) বছৰ
4 বছৰ পিছত অজয়ৰ বয়স হ’ব = {(x – 5) + 4} = (x − 1) বছৰ
প্রশ্নমতে, x + 4 = 2(x – 1)
⇒ x + 4 = 2x – 2
⇒ x – 2x = -2 – 4
⇒ -x = -6 (-1 ৰে হৰণ কৰি)
⇒ x = 6
∴ বিজয় বয়স = 6 বছৰ
অজয়ৰ বয়স = (6 – 5) বছৰ অৰ্থাত 1 বছৰ।
17. ৰমেনৰ দেউতাকৰ বয়স, ৰমেনৰ বয়সৰ 4 গুণ। 5 বছৰ পিছত ৰমেনৰ দেউতাকৰ বয়স ৰমেনৰ বয়সৰ 3 গুণ হ’লে তেওঁলোকৰ বৰ্তমান বয়স কিমান?
উত্তৰঃ ধৰা হ’ল, ৰমেনৰ বৰ্তমান বয়স x বছৰ
∴ দেউতাকৰ বর্তমান বয়স = 4x বছৰ
5 বছৰ পাঠত ৰমেনৰ বয়স (x + 5) বছৰ
5 বছৰ পাছত দেউতাকৰ বয়স (4x + 5) বছৰ
প্রশ্নমতে, 4x + 5 = 3(x + 5)
⇒ 4x + 5 = 3x + 15
⇒ 4x – 3x = 15 – 5
⇒ x = 10
∴ ৰমেনৰ বৰ্তমান 10 বছৰ
দেউতাকৰ বৰ্তমান বয়স 4 × 10 = 40 বছৰ
18. দুখন মেজ আৰু তিনিখন চকীৰ মুঠ দাম 705 টকা, এখন মেজৰ দাম চকীৰ দামতকৈ 40 টকা বেছি হ’লে মেজ আৰু চকীৰ দাম নিৰ্ণয় কৰা।
উত্তৰঃ ধৰা হ’ল, প্ৰথম চকীৰ দাম = x টকা
∴ এখন মেজৰ দাম (x + 40) টকা
প্রশ্নমতে, 2(x + 40) + 3x = 705
⇒ 3x + 80 + 3x = 705
⇒ 5x + 80 – 80 = 705 – 80
⇒ 5x = 625
⇒ 5x/5 = 625/5
⇒ x = 125
∴ এখন চকীৰ দাম = 125 টকা
মেজৰ দাম = (125 + 40) টকা = 165 টকা।
19. দুটা পূৰক কোণৰ মাপৰ পাৰ্থক্য 12° হ’লে কোণ দুটা নির্ণয় কৰা।
উত্তৰঃ ধৰাহ’ল, এটা কোণৰ মাপ = x°
∴ আনটো কোণৰ মাপ = (90° – x°)
প্রশ্নমতে, x – (90 – x) = 12
⇒ x – 90 + x = 12
⇒ 2x – 90 = 12
⇒ 2x – 90 + 90 = 12 + 90
⇒ 2x/2 = 102/2
⇒ x = 51
∴ এটা কোণৰ মাপ = 51°
আনটো কোণৰ মাপ (90° – 51°) = 39°
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

