SEBA Class 7 Mathematics (Assamese Medium) Chapter 11 – পৰিসীমা আৰু কালি Solutions & Summary
Find SEBA Class 7 Mathematics Chapter 11 – “পৰিসীমা আৰু কালি” (Perimeter and Area) solutions, designed for Assamese medium students. This chapter explains the concepts of measuring the perimeter and area of different shapes like squares, rectangles, triangles, circles, and irregular figures.
Students will learn about formula-based calculations for perimeter and area, unit conversions, and real-life applications such as land measurement, fencing, and tiling. The chapter also covers finding the area of composite figures and solving practical geometry problems.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students master measurement concepts and perform well in exams.
To access solutions for all chapters, Click Here
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীলনী – 11.1 |
|---|
1. তলত কেইটামান সামান্তৰিকৰ ভূমি, উন্নতি আৰু কালিৰ যিকোনো দুটা দিয়া আছে। আনটোৰ মাপ নির্ণয় কৰি খালী ঠাই পূৰোৱা।
|
সামান্তৰিক |
(i) |
(ii) |
(iii) |
(iv) |
(v) |
(vi) |
|---|---|---|---|---|---|---|
|
ভূমি |
10 চে.মি. |
20 চে.মি. |
15 চে.মি. |
_______ |
15.6 চে.মি. |
_______ |
|
উন্নতি |
7 চে.মি. |
_______ |
2.5 চি মি. |
2.5 ডেচি মি. |
_______ |
8.4 ডেচি মি. |
|
কালি |
______ |
400 বৰ্গ চে.মি. |
_______ |
325 বৰ্গ মি. |
16.38 বৰ্গ চে.মি. |
48.72 বৰ্গ ডেচি মি. |
উত্তৰঃ
|
সামান্তৰিক |
(i) |
(ii) |
(iii) |
(iv) |
(v) |
(vi) |
|---|---|---|---|---|---|---|
|
ভূমি |
10 চে.মি. |
20 চে.মি. |
15 চে.মি. |
1.3 ডে.মি. |
15.6 চে.মি. |
5.8 ডেচি মি. |
|
উন্নতি |
7 চে.মি. |
20 চে.মি. |
2.5 চে.মি. |
25 ডেচি মি. |
1.05 চে.মি. |
8.4 ডেচি মি. |
|
কালি |
70 বৰ্গ চে.মি. |
400 বৰ্গ চে.মি. |
37.5 বৰ্গ চে.মি. |
325 বৰ্গ মি. |
16.38 বৰ্গ চে.মি. |
48.72 বৰ্গ ডেচি মি. |
2. এটা ত্রিভুজৰ কালি (A), ভূমি (B) আৰু উন্নতি (H) বোৰৰ দুটাকৈ তলত দিয়া আছে। খালী ঠাই পূৰোৱা।
(i) A = 64 বর্গ চে.মি.
B = 8 চে.মি.
H = ___________
উত্তৰঃ A = 64 বর্গ চে.মি.
B = 8 চে.মি.
H = 16 চে.মি.
(ii) A = ___________
B = 3 মি
H = 214 চে.মি.
উত্তৰঃ A = 3.21 বৰ্গ মি.
B = 3 মি.
H = 214 চে.মি.
(iii) A = 94 বৰ্গ চে.মি.
B = ___________
H = 7 মি.
উত্তৰঃ A = 94 বৰ্গ চে.মি.
B = 0.269 চে.মি.
H = 7 মি.
(iv) A = 1256 বৰ্গ চে.মি.
B = __________
H = 31.4 মি.মি.
উত্তৰঃ A = 1256 বৰ্গ চে.মি.
B = 800 চে.মি.
H = 31.4 মি.মি.
(v) A = 16.38 বৰ্গ চে.মি.
B = 15.6 চে.মি.
H = ___________
উত্তৰঃ A = 16.38 বৰ্গ চে.মি.
B = 15.6 চে.মি.
H = 4.2 চে.মি.
3. প্রতিটো ট্রেপিজিয়ামৰ কালি নিৰ্ণয় কৰা।
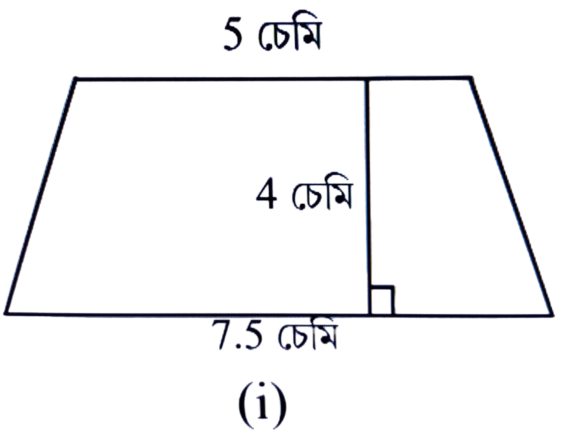
উত্তৰঃ দিয়া আছে,
ট্রেপিজিয়ামৰ সমান্তৰাল বাহুদুটা ক্রমে 5 চে.মি. আৰু 7.5 চে.মি.
উচ্চতা = 4 চে.মি.
∴ ট্রেপিজিয়ামৰ কালি = 1/2 × (সমান্তৰাল বাহৰ যোগফল) × উচ্চতা
= 1/2 × (5 + 7.5) × 4 বর্গ চে.মি.
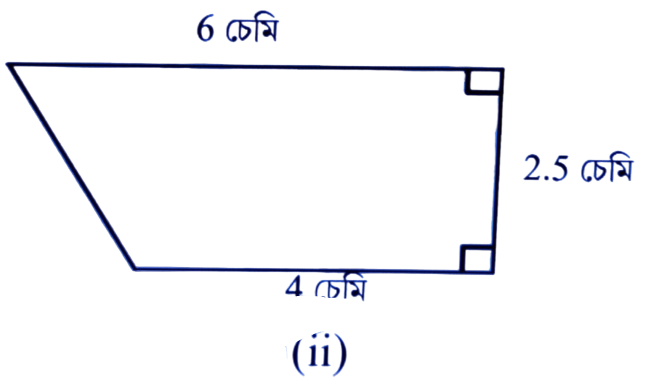
উত্তৰঃ চিত্রমতে, ট্রেপিজিয়ামটোৰ সমান্তৰাল বাহু ক্রমে 6 চে.মি. আৰু 4 চে.মি.
উচ্চতা = 2.5 চে.মি.
∴ ট্রেপিজিয়ামৰ কালি = 1/2 × (সমান্তৰাল বাহুৰ যোগফল) × উচ্চতা
= 1/2 × (6 চে. মি. + 4 চে.মি.) × 2.5 চে.মি.
= 1/2 × 10 চে.মি. × 2.5 চে.মি.
= 12.5 বর্গ চে.মি.
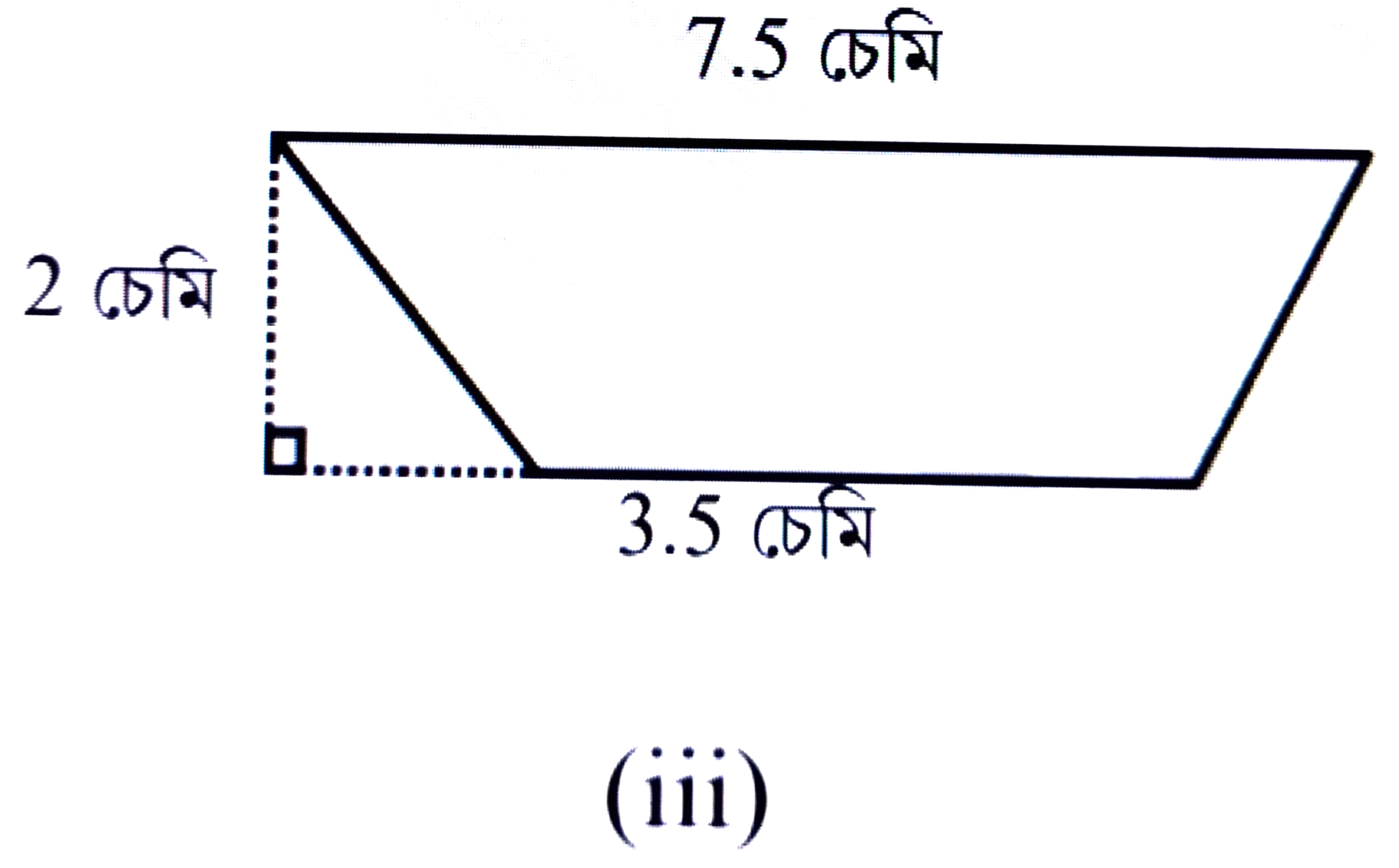
উত্তৰঃ চিত্রমতে, ট্রেপিজিয়ামটোৰ সমান্তৰাল বাহু ক্রমে 7.5 চে.মি. আৰু 3.5 চে.মি.
উচ্চতা = 2 চে.মি.
∴ ট্রেপিজিয়ামৰ কালি = 1/2 × (সমান্তৰাল বাহুৰ যোগফল) × উচ্চতা
= 1/2 × (7.5 + 3.5) × 2 চেমি.
= 1/2 × 11 × 2 বর্গ চে.মি.
= 11 বর্গ চে.মি.
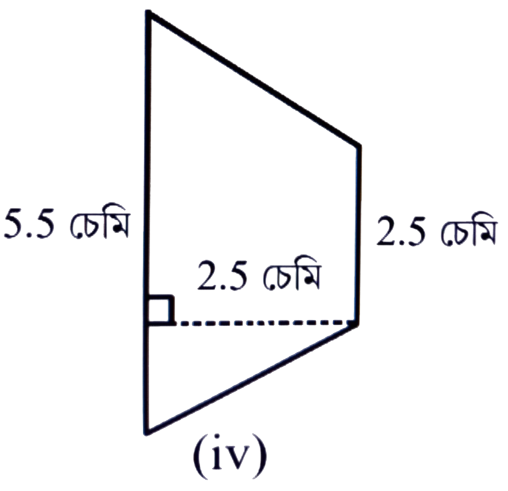
উত্তৰঃ চিত্রমতে, ট্রেপিজিয়ামটোৰ সমান্তৰাল বাহু ক্রমে 5.5 বৰ্গ চে.মি. আৰু 2.5 চে.মি.
উচ্চতা = 2.5 চে.মি.
∴ ট্রেপিজিয়ামৰ কালি = 1/2 × (সমান্তৰাল বাহুৰ যোগফল) × উচ্চতা
= 1/2 × (5.5 + 2.5) × 2.5 বর্গ চেমি.
= 1/2 × 8.0 × 2.5 বর্গ চে.মি.

4. তলত কেইটামান ৰম্বাছৰ ভূমি, উন্নতি বা কৰ্ণ দুডালৰ দীঘ দিয়া আছে। বিভিন্ন সূত্ৰ ব্যৱহাৰ কৰি তালিকাখন পূৰোৱা।
|
ক্ৰমিক নং |
ভূমি |
উন্নতি |
এডাল কৰ্ণ |
আনডাল কৰ্ণ |
কালি |
|---|---|---|---|---|---|
|
(i) |
10 চে.মি. |
8.2 চে.মি. |
________ |
||
|
(ii) |
8 চে.মি. |
________ |
56 বৰ্গ মি. |
||
|
(iii) |
20 চে.মি. |
7 চে.মি. |
________ |
||
|
(iv) |
18 চে.মি. |
14 চে.মি. |
________ |
||
|
(v) |
2.7 চে.মি. |
________ |
4.725 বৰ্গ চে.মি. |
||
|
(vi) |
_________ |
30 চে.মি. |
120 বৰ্গ চে.মি. |
উত্তৰঃ (i) ৰম্বাচৰ কালি = 1/2 × কৰ্ণ দুডালৰ পূৰণফল
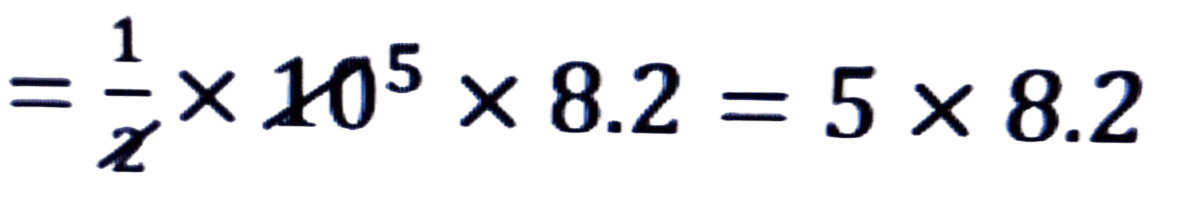
= 41.0 = 41 বর্গ চে. মি.
(ii) ৰম্বাচৰ কালি = ভূমি × উন্নতি
⇒ 56 বর্গ চে. মি. = 8 চে. মি. × উন্নতি
⇒ উন্নতি = 56 বর্গ চে.মি./8 চে.মি. = 7 চে. মি.
(iii) ৰম্বাচৰ কালি = ভূমি × উন্নতি
= (20 × 7) = 70 বর্গ চে.মি.
(iv) ৰম্বাচৰ কালি = 1/2 × কৰ্ণ দুডালৰ পূৰণফল
= 1/2 × (18 × 14) বর্গ চে.মি.
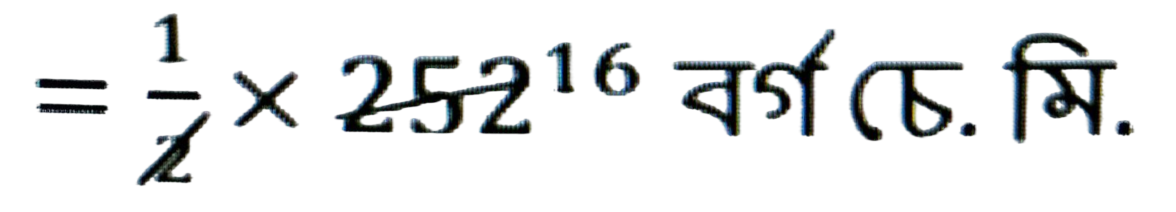
= 126 বর্গ চে.মি.
(v) ৰম্বাচৰ কালি = ভূমি × উন্নতি
⇒ 7.725 বর্গ চে.মি. = 2.7 চে.মি. × উন্নতি
⇒ উন্নতি = 1/2 × (কৰ্ণ দুডালৰ পূৰণফল)
(vi) ৰম্বাচৰ কালি = 1/2 × (কৰ্ণ দুডালৰ পূৰণফল)
⇒ 120 বর্গ চে.মি. = 1/2 × 30 × আনডাল কর্ণ
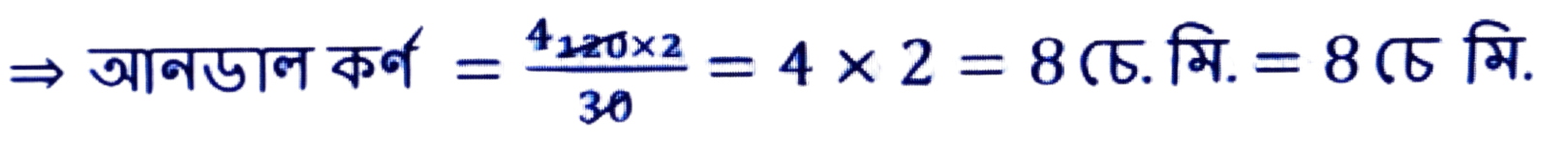
5. এটা সামান্তৰিকৰ ভূমিৰ জোখ 1 মি 50 চে.মি. আৰু উচ্চতা 75 চেমি। ইয়াৰ কালি বর্গ মিটাৰত উলিওৱা।
উত্তৰঃ দিয়া আছে সামন্তৰিকটোৰ ভূমিৰ জোখ = 1 মি. 50 চে.মি.
= 150 চে.মি
উচ্চতা = 75 চে.মি.
∴ সামন্তৰিকটোৰ কালি = ভূমি × উচ্চতা
= 150 চে.মি. × 75 চে.মি.
= 11250 বর্গ চে.মি.
= 11250/(100 × 100) বর্গ মি. = 1.125 বর্গ মি.
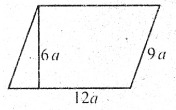
6. এটা সামান্তৰিকৰ ওচৰা-ওচৰি বাহু দুটাৰ জোখ 12 চে.মি. আৰু 9 চে.মি। দীঘল বাহু দুটাৰ মাজৰ লম্ব দূৰত্ব 6 চে.মি.। সামান্তৰিকটোৰ কালি নিৰ্ণয় কৰা। (চিত্র আঁকি ল’বা)
উত্তৰঃ দিয়া আছে, সামন্তৰিকটোৰ ভূমি = 12 চে.মি
উচ্চতা = 6 চে.মি.
∴ সামন্তৰিকটোৰ কালি = ভূমি × উচ্চতা
= 12 × 6 বর্গ চে.মি. = 72 বর্গ চে.মি.
7. এটা সমকোণী ত্রিভুজৰ কালি 30 বর্গ চে.মি.। সমকোণ উৎপন্ন কৰা এটা বাহুৰ দীঘ 6 চে.মি. হ’লে সমকোণ উৎপন্ন কৰা আনটো বাহুৰ দীঘ নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে ত্রিভুজটোৰ কালি = 30 বর্গ চে.মি.
ধৰা হ’ল, ত্রিভুজটোৰ তুমি = 6 চে.মি
∴ 1/2 × ভূমি × উচ্চতা = কালি
⇒ 1/2 × 6 × উচ্চতা = 30
⇒ উচ্চতা = 30 বর্গ চে.মি./3 চে.মি. = 10 চে.মি.
∴ সমকোণ উৎপন্ন কৰা আনটো বাহুৰ দীঘ = 10 চে.মি.
8. ABC এটা সমদ্বিবাহু ত্রিভুজ য’ত AB = AC = 7.5 চে.মি. আৰু BC = 9 চে.মি. (চিত্ৰ চোৱা) A ৰ পৰা BC লৈ টনা AD ৰ উচ্চতা 6 চে.মি.। ∆ABC ৰ কালি উলিওৱা। C ৰ পৰা AB লৈ টনা উচ্চতা CE কিমান হ’ব?
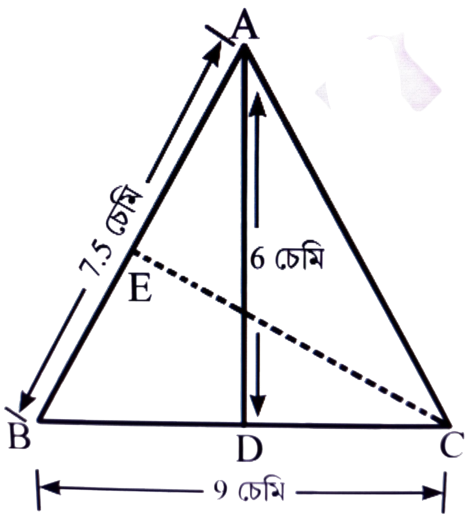
উত্তৰঃ দিয়া আছে, ABC সমদ্বিবাহু ত্রিভুজৰ AB = AC = 7.5 চে.মি.
ভূমি BC = 9 চে.মি. উচ্চতা AD = 6 চে.মি.
∴ ABC ত্রিভুজৰ কালি = 1/2 × ভূমি × উচ্চতা
= 1/2 × 9 × 6 = 27 বৰ্গ চে.মি.
আকৌ, 1/2 × AB × CE = ∆ABC ৰ কালি
⇒ 1/2 × 7.5 × CE = 27
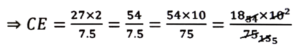
= (36 × 2)/(5 × 2) = 72/10 = 7.2
∴ উচ্চতা CE = 7.2 চে.মি.
9. ABC সমকোণী ত্রিভুজৰ ∠A = 90°। AD, BC ৰ ওপৰত লম্ব। যদি AB = 12 চে.মি., AC = 5 চে.মি. BC = 13 চে.মি. হয় তেন্তে-
(i) ABC ত্রিভুজৰ কালি। আৰু
উত্তৰঃ দিয়া আছে, ABC সমকোণী ত্রিভুজৰ ∠A = 90°
AD ⏊ BC. আৰু AB = 12 চে.মি. AC = 5 চে.মি.
BC = 13 চে.মি.
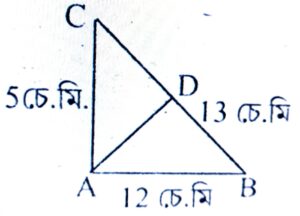
∆ABC ৰ কালি = 1/2 × AB × AC
= 1/2 × 12 × 5 = 30 বর্গ চে.মি.
(ii) AD ৰ দৈৰ্ঘ্য নির্ণয় কৰা।
উত্তৰঃ দিয়া আছে, ABC সমকোণী ত্রিভুজৰ ∠A = 90°
AD ⏊ BC. আৰু AB = 12 চে.মি. AC = 5 চে.মি.
BC = 13 চে.মি.
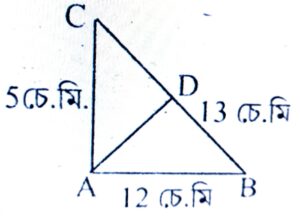
1/2 × BC × AD = ∆ABC ৰ কালি
⇒ 1/2 × 13 × AD = 30
⇒ AD = (30 × 2)/13 = 60/13
10. ABCD চতুর্ভুজৰ AC কৰ্ণৰ দীঘ 12 মি। যদি BL ⏊ AC, DM ⏊ AC যাতে BL = 3 মি, DM = 7 মি তেন্তে ABCD চতুর্ভুজৰ কালি কিমান?
উত্তৰঃ
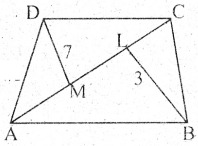
দিয়া আছে, ABCD চতুর্ভুজৰ কৰ্ণ AC = 12 মি.
BL ⏊ AC, DM ⏊ AC
য’ত BL = 30 মি., DM = 7 মি.
∴ ABCD ৰ কালি = 1/2 × কৰ্ণ × শাখা লম্বৰ সমষ্টি
= 1/2 × 12 × (3 + 7)
= 6 × 10 = 60
∴ ABCD ৰ কালি = 60 বর্গ মি.
11. EFGH চতুর্ভুজৰ EG কৰ্ণ। EG ৰ ওপৰত FM আৰু HN লম্ব। EG = 28 চে.মি., FM = 7চে.মি. HN = 5 চে.মি. হ’লে নির্ণয় কৰা।
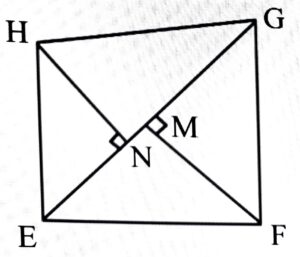
(i) EFG ত্রিভুজৰ কালি।
উত্তৰঃ দিয়া আছে, EFGH চতুর্ভুজৰ EG কর্ণ কালি।
FM ⏊ EG, HN ⏊ EG;EG = 28 চে.মি. FM = 7 চে.মি.
HN = 5 চে.মি.
∆EFG ৰ কালি = 1/2 × EG × FG
= 1/2 × 28 × 7 বর্গ চে.মি.
= 14 × 7 বর্গ চে.মি. = 98 বর্গ চে.মি.
(ii) EHG ত্রিভুজৰ কালি।
উত্তৰঃ ∆EHG ৰ কালি = 1/2 × EG × HN
= 1/2 × 28 × 5 বর্গ চে.মি. = 14 × 5 = 70 বর্গ চে.মি.
(iii) EFGH চতুর্ভুজৰ কালি।
উত্তৰঃ EFGH চতুর্ভুজৰ কালি = 1/2 × কর্ণ × শাখা লম্ব সমষ্টি
= 1/2 × 28 × (7 + 5) = 14 × 12 = 168 বর্গ চে.মি.
12. এটা চতুর্ভুজৰ কালি 11 বৰ্গ চে.মি.। কৰ্ণ এডালৰ ওপৰত টনা শাখা লম্ব দুডাল ক্রমে 2.5 চে.মি. আৰু 1.5 চে.মি.। সেই কৰ্ণ ডালৰ দৈর্ঘ্য নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, চতুর্ভুজৰ কালি = 11 বর্গ চে.মি.
চতুর্ভুজটোৰ শাখা লম্ব দুডাল ক্রমে 2.5 চে.মি. আৰু 1.5 চে.মি.
∴ 1/2 × কর্ণ × শাখা লম্ব সমষ্টি = 11
⇒ 1/2 × কর্ণ × (2.5 + 1.5) = 11
![]()
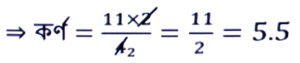
∴ চতুর্ভুজটোৰ কৰ্ণডালৰ দৈর্ঘ্য 5.5 চে.মি
13. এটা ট্রেপিজিয়ামৰ সমান্তৰাল বাহু দুডালৰ মাপ 18 চে.মি. আৰু 16 চে.মি.। সমান্তৰাল বাহু দুডালৰ মাজৰ দূৰত্ব 8 চে.মি.। ট্রেপিজিয়ামটোৰ কালি নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, ট্রেপিজিয়ামৰ সমান্তৰাল বাহু দুটাৰ মাপ ক্রমে 8 চে.মি. আৰু 16 চে.মি.।
সমান্তৰাল বাহু দুচাৰ মাজৰ দূৰত্ব = 8 চে.মি.
∴ ট্রেপিজিয়ামৰ কালি = 1/2 × সমান্তৰাল বাহুৰ মাজৰ দূৰত্ব × সমান্তৰাল বাহু দুটাৰ যোগফল
= 1/2 × 8 × (8 + 16)
= 1/2 × 4 × 24 = 2 × 24 = 48 বর্গ চে.মি.।
14. ট্রেপিজিয়াম আকৃতিৰ পথাৰ এখনৰ কালি 600 বর্গ মি.। সমান্তৰালভাৱে থকা পাৰ দুটাৰ দীঘ 20 মিটাৰ আৰু 30 মিটাৰ। সমান্তৰাল পাৰ দুটাৰ মাজৰ দূৰত্ব নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, ট্রেপিজিয়াম আকৃতিৰ পথাৰখনৰ কালি 600 বর্গ মি.
সমান্তৰাল পাৰ দুটাৰ দীঘ ক্ৰমে 20 মি. আৰু 30 মি.
প্রশ্নমতে, 1/2 × সমান্তৰাল বাহু দুটাৰ মাজৰ দূৰত্ব × (সমান্তৰাল বাহু দুটাৰ যোগফল = কালি)
⇒ 1/2 × সমান্তৰাল বাহু দুটাৰ মাজৰ দূৰত্ব × (20 × 30) = 600

∴ সমান্তৰাল পাৰ দুটাৰ মাজৰ দূৰত্ব = 24 মি.
15. ট্রেপিজিয়াম আকৃতিৰ কাগজ এখনৰ কালি 11 বৰ্গ চে.মি., ইয়াৰ সমান্তৰাল বাহু দুটাৰ মাজৰ দূৰত্ব 5.5 চে.মি. আৰু সমান্তৰাল বাহু এটাৰ দৈর্ঘ্য 2.5 চে.মি.। আনডাল সমান্তৰাল বাহুৰ দৈর্ঘ্য উলিওৱা।
উত্তৰঃ দিয়া আছে, ট্রেপিজিয়াম আকৃতিৰ কাগজখনৰ কালি 11 বৰ্গ চে.মি.
সমান্তৰাল বাহুদুটাৰ মাজৰ দূৰত্ব = 5.5 চে.মি.
এটা বাহুৰ দৈর্ঘ্য = 2.5 চে.মি.
প্রশ্নমতে, 1/2 × সমান্তৰাল বাহু দুটাৰ মাজৰ দূৰত্ব × (সমান্তৰাল বাহু দুটাৰ যোগফল = কালি)
⇒ 1/2 × 5.5 × (2.5 + 1) = 11, য’ত 1 = আনবাহুৰ দৈর্ঘ্য
⇒ 2.5 + l = (2 × 11)/5.5 = (22 × 10)/55 = 220/55
⇒ l = 220/55 – 2.5
⇒ l = 220/55 – 25/10 ⇒ l = 44/11 – 5/2
⇒ l = (88 – 55)/22 ⇒ l = 33/22
⇒ l = 33/22 ⇒ l = 3/2 ⇒ l = 1.5
∴ আনডাল সমান্তৰাল বাহুৰ দৈর্ঘ্য = 1.5 চে.মি.
16. এটা ৰম্বাছৰ কালি উলিওৱা যাৰ কৰ্ণ দুডালৰ দৈর্ঘ্য 7 মিটাৰ আৰু 6 মিটাৰ। কালিৰ পৰিমাণ বৰ্গ চেন্টিমিটাৰত লিখিবা।
উত্তৰঃ দিয়া আছে, ৰম্বাছটোৰ কৰ্ণ (h₁) = 7 মি. = 700 চে.মি.
আৰু কৰ্ণ (h₂) = 6 মি. = 600 চে.মি.
∴ ৰম্বাছটোৰ কালি = 1/2 × h₁× h2
= 1/2 × 700 × 600 = 210000 বর্গ চে.মি.
17. এটা ৰম্বাছৰ কালি উলিওৱা যাৰ বাহুৰ দৈৰ্ঘ্য 6 চে.মি. আৰু উন্নতি 8 চে.মি.। যদি ইয়াৰ এডাল কৰ্ণৰ দৈর্ঘ্য 8 চে.মি. হয়, আনডাল কৰ্ণৰ দৈৰ্ঘ্য কিমান হ’ব নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, ৰম্বাছৰ বাহু (b) = 6 চে.মি.
ৰম্বাছৰ উচ্চতা, h = 8 চে.মি
∴ ৰম্বাছটোৰ কালি = বাহু × উচ্চতা
= b × h = 6 × 8 বর্গ চে.মি. = 48 বর্গ চে.মি.
আকৌ, ৰম্বাছটোৰ এডাল কৰ্ণ (h₁) = 8 চে.মি.
আনডাল কর্ণ = (h₂) = ?
প্রশ্নমতে, 1/2 × কৰ্ণ (h₁) × কৰ্ণ (h₂) = ৰম্বাছৰ কালি
⇒ 1/2 × 8 × h₂ = 48
⇒ h₂ = (48 × 2)/8 = 12
∴ ৰম্বাছটোৰ আনডাল কর্ণ (h₂) = 12 চে.মি.
18. এটা ৰম্বাছৰ কালি 56 বর্গ মিটাৰ। ইয়াৰ পৰিসীমা 32 মি হ’লে উচ্চতা কিমান হ’ব উলিওৱা।
উত্তৰঃ দিয়া আছে, ৰম্বাছটোৰ কালি = 56 বর্গ মি.
ৰম্বাছটোৰ পৰিসীমা = 32 মি.
∴ 4 × বাহু = 32 মি. ⇒ বাহু = 32/4 মি.
∴ ৰম্বাদটোৰ বাহু দৈর্ঘ্য = 8 মি.
প্রশ্নমতে, বাহু × উচ্চতা = ৰম্বাছ কালি
⇒ 8 মি. × উচ্চতা = 56 বর্গ মি.
⇒ উচ্চতা = 56/8 = 7 মি.
∴ ৰম্বাছটোৰ উচ্চতা = 7 মি.
19. এটা ৰম্বাছৰ কৰ্ণ 6 মিটাৰ, ইয়াৰ কালি 24 বর্গ মিটাৰ হ’লে বাকীটো কৰ্ণৰ দীঘ কিমান হ’ব?
উত্তৰঃ দিয়া আছে, ৰম্বাছটোৰ কালি = 24 বর্গ মি.
ৰম্বাছটোৰ এটা কৰ্ণ = (h₁) = 6 মি.
প্রশ্নমতে, 1/2 × কর্ণ (h₁) × কৰ্ণ (h₂) = ৰম্বাছৰ কালি
⇒ 1/6 × 6 মি. × কর্ণ (h₂) = 24 বর্গ মি.
⇒ কর্ণ (h₂) = (24 × 2)/6 মি.
কর্ণ (h₂) = 8 মি.
∴ ৰম্বাছটোৰ বাকীটো কৰ্ণৰ দীঘ = 8 মি.
20. এটা সামান্তৰিকৰ কালি 15 বর্গ চে.মি., ভূমি 5 চে.মি. হ’লে উচ্চতা কিমান?
উত্তৰঃ দিয়া আছে, সামন্তৰিক কালি = 15 বর্গ চে.মি.
সামন্তৰিকৰ ভূমি = 5 চে.মি.
প্রশ্নমতে, ভূমি × উচ্চতা = সামন্তৰিকৰ কালি
⇒ 5 চে.মি. × উচ্চতা = 15 বর্গ চে.মি.
⇒ উচ্চতা = 15/5 চে.মি. = 3 চে.মি.
∴ সামন্তৰিকটোৰ উচ্চতা = 3 চে.মি.।
অনুশীলনী – 11.2 |
|---|
1. তলত দিয়া ব্যাস ব্যৱহাৰ কৰি বৃত্তবোৰৰ পৰিধি উলিওৱা (π = 22/7)
(a) 28 চে.মি.
উত্তৰঃ দিয়া আছে, বৃত্তটোৰ ব্যাস (d) = 28 চে.মি.
∴ বৃত্তটোৰ ব্যাসার্ধ (r) = 28/2 চে.মি. = 14 চে.মি.
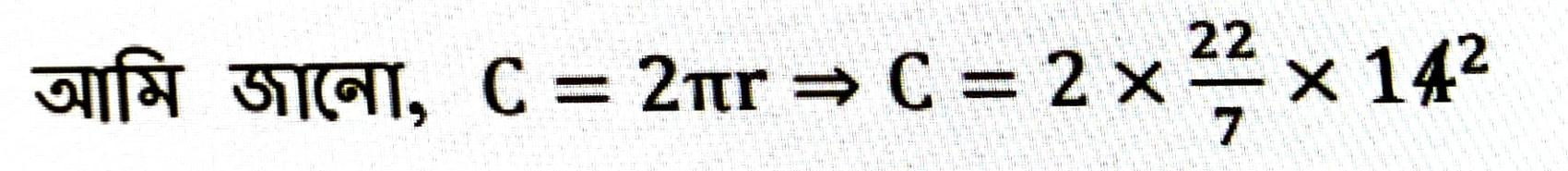
⇒ C = 88 চে.মি.
(b) 56 মি.মি.
উত্তৰঃ দিয়া আছে, বৃত্তটোৰ ব্যাস (d) = 56 মি.মি.
∴ বৃত্তটোৰ ব্যাসার্ধ (r) = 56/2 মি.মি. = 28 মি.মি.
আমি জানো, C = 2πr
⇒ C = 2 × 22/7 × 28
![]()
⇒ C = 176
∴ নির্ণেয় পৰিধি = 176 মি.মি.
(c) 42 চে.মি.
উত্তৰঃ দিয়া আছে, বৃত্তটোৰ ব্যাস (d) = 42 চে.মি.
∴ বৃত্তটোৰ ব্যাসার্ধ (r) = 44/2 চে.মি. = 21 চে.মি.
আমি জানো, C = 2πr
⇒ C = 2 × 22/7 × 21
![]()
∴ নির্ণেয় পৰিধি = 132 চে.মি.
2. 14 মিটাৰ ব্যাসার্ধৰ বৃত্তাকৃতি বাগিচা এখনত কাঁটাতাঁৰৰ বেৰ (fence) দিবলৈ কিমান দৈৰ্ঘ্যৰ তাঁৰৰ প্ৰয়োজন হ’ব? প্রতিমিটাৰ কাঁটাতাঁৰৰ দাম 55.00 টকা হ’লে বাগিচাখন বেৰোতে কিমান খৰচ পৰিব? (π = 22/7)
উত্তৰঃ দিয়া আছে, বৃত্তাকৃতিবাগিচাখনৰ ব্যাসার্ধ (r) = 14 মিটাৰ
∴ c = 2πr
![]()
∴ বাগিচাখনত কাটা তাঁৰৰ বেৰ দিবলৈ 88 মিটাৰ দৈৰ্ঘ্যৰ বেৰৰ প্ৰয়োজন হ’ব।
আকৌ, 1 মিটাৰ কাঁটা তাঁৰৰ দাম = 55.00 টকা
∴ বাগিচাখন বেৰোতে খৰচ পৰিব = 88 × 55 টকা = 4840 টকা
∴ বাগিচাখন বেৰোতে খৰচ পৰিব = 4840 টকা।
3. কাষৰ চিত্ৰত দিয়া জোখমতে অর্ধাবৃত্তাকৃতি ক্ষেত্ৰখনৰ পৰিসীমা নিৰ্ণয় কৰা।

উত্তৰঃ চিত্রমতে, অর্ধাবৃত্তাকৃতি ক্ষেত্ৰখনৰ ব্যাস (d) = 10 চে.মি.
∴ অৰ্ধাবৃত্তাকাৰ ক্ষেত্ৰখনৰ ব্যাসার্ধ (r) = 10/2 চে.মি. = 5 চে.মি.
∴ ক্ষেত্ৰখনৰ পৰিধি = c/2 + r = 2πr/2 + r = πr + r
= 22/7 × 5 + 5
= 3.14 × 5 + 5
= 15.70 + 5 = 20.7
∴ নির্ণয়ে অর্ধবৃত্তাকাৰ ক্ষেত্ৰখনৰ পৰিধি = 20.7 চে.মি
4. গাড়ীৰ চকা এটাৰ ব্যাস 70 চে.মি.। গাড়ীখনে 33 কিমি অতিক্রম কৰিলে চকাটোৱে কিমান পাক ঘুৰিব লাগিব। (π = 22/7)
উত্তৰঃ দিয়া আছে, চকাটোৰ ব্যাস (d) = 70 চে.মি.
∴ চকাটোৰ ব্যাসার্ধ (r) = d/2 = 70 চে.মি./2 = 35 চে.মি.
∴ চকাটোৰ পৰিধি c = 2πr
= 2 × 22/7 × 35
= 2 × 22/7 = 35⁵ = 220 চে.মি.
∴ 33 কি.মি. অতিক্ৰম কৰিবলৈ চকাটোৱে ঘূৰিব = 33 কি.মি/220 চে.মি.
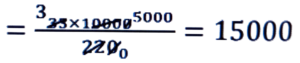
∴ 33 কি.মি. অতিক্ৰম কৰিবলৈ চকাটোৱে 15,000 পাক ঘূৰিব লাগিব।
5. এটা বৃত্তৰ ব্যাসার্ধ 84 চে.মি. আৰু আন এটা বৃত্তৰ ব্যাসার্ধ 91 চে.মি.। দ্বিতীয় বৃত্তটোৰ পৰিধি প্ৰথমটোতকৈ কিমান বেছি নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, প্রথম বৃত্তৰ ব্যাসার্ধ (r₁) = 81 চে.মি.
2য় বৃত্তৰ ব্যাসার্ধ (r₂) = 91 চে.মি.
∴ ২য় বৃত্তৰ পৰিধি, প্রথমটোতকৈ বেছি হ’ব
= C₂ – C₁
= 5πr₂ – 2πr₁
= 2 × 22/7 × 91 – 2 × 22/7 × 81
= 2 × 22/7 × (91 – 81)
= 2 × 3.14 × 10
![]()
∴ ২য় বৃত্তৰ পৰিধি, প্রথমটোতকৈ 62.8 বেছি।
6. এটা বর্গৰ বাহুৰ দীঘ 3 মিটাৰ আৰু এটা বৃত্তৰ ব্যাসার্ধ 7 মিটাৰ। বৰ্গৰ পৰিসীমা আৰু বৃত্তটোৰ পৰিধিব পার্থক্য কিমান মিটাৰ হ’ব?
উত্তৰঃ দিয়া আছে, এটা বৰ্গৰ বাহুৰ দীঘ = 3 মিটাৰ
আৰু বৃত্ত এটাৰ ব্যাসার্ধ = 7 মিটাৰ
∴ বৰ্গৰ পৰিসীমা আৰু বৃত্তটোৰ পৰিধিৰ পার্থক্য
= 2πr – 4 × বাহু
![]()
∴ নির্ণয়ে পার্থক্য = 32 মিটাৰ
7. ৰুণিমাই 44 চে.মি. দৈর্ঘ্যৰ তাঁৰ এডাল লৈছিল আৰু ইয়াক বৃত্ত আকৃতিত ভাঁজ দিছিল। বৃত্তটোৰ ব্যাস কিমান চে.মি. হ’ব? একেডাল তাঁৰেৰে যদি এটা বৰ্গৰ আকৃতিত ভাঁজ দিয়া হয় তেন্তে বৰ্গটোৰ প্ৰত্যেক বাহুৰ দৈর্ঘ্য কিমান হ’ব?
উত্তৰঃ দিয়া আছে, বৃত্তটোৰ পৰিধি (C) = 44 চে.মি.
অৰ্থাৎ, 2πr = 44 ⇒ 2 × 22/7 × r = 44
⇒ 2r = (44 × 7)/22
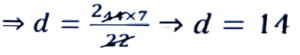
∴ বৃত্তটোৰ ব্যাস = 14 চে.মি.
প্রশ্নমতে, বৰ্গটোৰ পৰিসীমা = বৃত্তৰ পৰিধি
⇒ 4 × বাহু = C
⇒ 4 × বাহু = 44
⇒ বাহু = 44/4 ⇒ বাহু = 11
∴ বৰ্গটোৰ প্ৰত্যেকটো বাহুৰ দৈর্ঘ্য = 11 চে.মি.
8. এখন গাড়ীৰ চকাৰ ব্যাস 98 চে.মি.। চকাটো 300 পাক ঘূৰিলে কিমান দূৰ বাট অতিক্ৰম কৰিব নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, গাড়ীৰ চকাৰ ব্যাস (d) = 98 চে.মি.
∴ ব্যাসার্ধ (r) = 98/2 চে.মি. = 49 চে.মি.
∴ চকাটোৰ পৰিধি (C) = 2πr
![]()
∴ 300 পাক ঘূৰিলে চকাটোৱে অতিক্ৰম কৰা বাট = 300 × 308 চে.মি.
= 92400 চে.মি.
∴ 300 পাক ঘূৰিবলৈ চকাটোৱে 92400 চে.মি. অতিক্ৰম কৰিব লাগিব।
9. বৃত্তাকৃতি বাগিচা এখনৰ চাৰিওপিনে জেওৰা দিওঁতে মুঠতে 2640 টকা খৰচ হ’ল। প্রতি মিটাৰ জেওৰাৰ খৰচ 28 টকা হ’লে বাগিচাখনৰ পৰিধি কিমান মিটাৰ হ’ব?
উত্তৰঃ দিয়া আছে, বৃত্তকৃতি বাগিচাখনৰ চাৰিওপিনে জেওৰা দিওঁতে মুঠ খৰচ = 2640 টকা
আৰু প্ৰতিমিটাৰ জেওৰাৰ খৰচ = 28 টকা
∴ বাগিচাখনৰ পৰিধি (C) 2640 টকা/28 টকা = 2640 টকা/28 টকা মিটাৰ
∴ (C) = 2640/28 = 98.2857 = 98.29 মিটাৰ (প্ৰায়)
10. 10 চে.মি. ব্যাসার্ধৰ কাগজ এটুকুৰাৰ পৰা 4 চে.মি. ব্যাসার্ধৰ কাগজ এটুকুৰা কাটি পেলাই দিয়া হ’ল। কাটি পেলোৱা টুকুৰাটোৰ পৰিধি প্রথম কাগজ টুকুৰাৰ পৰিধিতকৈ কিমান সৰু?
উত্তৰঃ দিয়া আছে, প্রথম বৃত্তটোৰ ব্যাসার্ধ (r₁) = 10 চে.মি.
২য় বৃত্তটোৰ ব্যাসার্ধ (r₂) = 4 চে.মি.
∴ প্ৰথম বৃত্তটোৰ পৰিধি ২য় টোতকৈ ডাঙৰ হ’ব
= C₁ – C₂ = 2πτ₁ – 2πr₂
= 2π(r₁ – r₂)
= 2 × 22/7 × (10 – 4) = 2 × 22/7 × 6
= 2 × 3.14 × 6 = 37.68 চে.মি.
অনুশীলনী – 11.3 |
|---|
1. শুদ্ধ উত্তৰটো লিখাঃ
(i) 10.5 চে.মি. ব্যাসার্ধৰ বৃত্ত এটাৰ কালি হ’ব-
(a) 346.5 বর্গ চে.মি.।
(b) 340.5 বর্গ চে.মি.।
(c) 34.65 বর্গ চে.মি.।
(d) 34.05 বর্গ চে.মি.।
উত্তৰঃ (a) 346.5 বর্গ চে.মি.।
(ii) বৃত্তাকৃতিৰ কাগজ এখনৰ কালি 616 বৰ্গ চে.মি. হ’লে কাগজখনৰ ব্যাসার্ধ হ’ব।
(a) 7 চে.মি.।
(b) 28 চে.মি.।
(c) 14 চে.মি.।
(d) 3.5 চে.মি.।
উত্তৰঃ (c) 14 চে.মি.।
2. তলত দিয়া ব্যাসার্ধ ব্যৱহাৰ কৰি বৃত্তবোৰ অংকন কৰি কালি নির্ণয়। য় কৰা (π = 22/7 ল’বা)
(a) 5 চে.মি.।
উত্তৰঃ দিয়া আছে, r = 5 চে.মি.
∴ বৃত্তটোৰ কালি = πr²
= 22/7 × 5 × 5 = 78.5714
= 78.57 বর্গ চে.মি. (প্রায়)
(b) 46 চে.মি.।
উত্তৰঃ দিয়া আছে, r = 4.6 চে.মি.
∴ বৃত্তটোৰ কালি = πr²
= 22/7 × 4.6 × 4.6
= 465.52/7 = 66.502857
= 66.50 বর্গ চে.মি. (প্রায়)
(c) 5.5 মিটাৰ।
উত্তৰঃ দিয়া আছে, r = 5.5 মিটাৰ
∴ বৃত্তটোৰ কালি = πr²
= 22/7 × 5.5 × 5.5
= 665.5/7= 95.07142
= 95.07 মিটাৰ² (প্রায়)
3. তলৰ বৃত্তবোৰৰ কালি দিয়া আছে, ব্যাসার্ধ আৰু ব্যাস নিৰ্ণয় কৰা।
(a) 154 বর্গ চে.মি.।
উত্তৰঃ দিয়া আছে, বৃত্তৰ কালি = 154 বৰ্গ চে.মি.
∴ πr² = 154 ⇒ 22/7 × r² = 154
⇒ r² = (154 × 7)/22
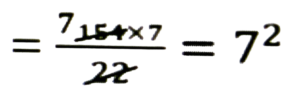
∴ r = 7
∴ বৃত্তটোৰ ব্যাসার্ধ = 7 চে.মি.
ব্যাস = 2r = 2 × 7 চে.মি. = 14 চে.মি.
(b) 550/7 বর্গ চে.মি.।
উত্তৰঃ দিয়া আছে, বৃত্তৰ কালি 550/7 বর্গ চে.মি.
∴ πr² = 550/7 ⇒ 22/7 × r² = 550/7
⇒ r² = 550/7 × 7/22
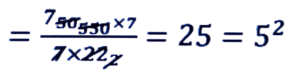
∴ r = 5 চে.মি.
∴ বৃত্তটোৰ ব্যাসার্ধ = 5 চে.মি.
ব্যাস = 2r চে.মি. = 2 × 5 চে.মি. = 10 চে.মি.
4. 3 মিটাৰ ব্যাসৰ এখন বৃত্তাকৃতিৰ টেবুলত ৰং লগাওঁতে কিমান খৰচ হ’ব, যদিহে প্ৰতি বর্গমিটাৰত খৰচ হয় 30 টকা ( π = 3:14 লোৱা)
উত্তৰঃ দিয়া আছে, বৃত্তৰ ব্যাস = 3 মি.
∴ বৃত্তটোৰ ব্যাসার্ধ = 1.5 মি.
∴ বৃত্তকাৰ টেবুলখনৰ কালি = πr²
= 22/7 × 1.5 × 1.5 বর্গ মি.
= 7.0714285 = 7.07 বর্গ মি.
প্রশ্নমতে, 1 বৰ্গমিটাৰৰ ৰং কৰা খৰচ = 30 টকা
∴ ৰং কৰা মুঠ খৰচ = 30 × 7.071 টকা = 212.14 টকা।
5. এটা বৃত্তৰ ব্যাসার্ধ 84 চে.মি. আৰু আন এটা বৃত্তৰ ব্যাসার্ধ 91 চে.মি.। দ্বিতীয় বৃত্তটোৰ কালি প্রথমটোতকৈ কিমান বেছি নির্ণয় কৰা। (π = 22/7 ল’বা)
উত্তৰঃ দিয়া আছে, প্ৰথম বৃত্তৰ ব্যাসার্ধ (r₁) = 84 চে.মি.
২য় বৃত্তৰ ব্যাসার্ধ (r₁) = 91 চে.মি.
∴ 2য় বৃত্তৰ পৰিধি, প্রথমটোতকৈ বেছি হ’ব πr²₂ – π²₁
= 22/7 (91)² – 22/7(84)²
= 26026 – 22176
= 3850 বর্গ চে.মি.
6. 28 চে.মি. তাঁৰেৰে তৈয়াৰ কৰা বৃত্ত এটা ভাঁজ কৰি এটা বৰ্গ তৈয়াৰ কৰা হ’ল।
(a) বৰ্গ আৰু বৃত্তৰ কালি নিৰ্ণয় কৰা।
উত্তৰঃ প্রশ্নমতে, বৃত্তটোৰ পৰিধি = 28 চে.মি.
∴ 2πr = 28
⇒ 2 × 22/7 × r = 28 ⇒ r = (28 × 7)/(2 × 22)
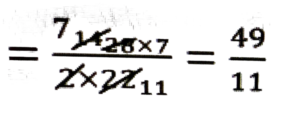
∴ বৃত্তটোৰ ব্যাসার্ধ (r) = 49/11 চে.মি.
∴ বৃত্তটোৰ কালি πr² = 22/7 × (49/11)²
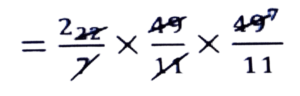
= 686/11 = 62.3636 = 62.36 বর্গ চে.মি.
আকৌ, বৰ্গৰ পৰিসীমা = 28 চে.মি.
∴ 4 × বাহু = 28
⇒ বাহু = 28/4
⇒ বাহু = 7
∴ বৰ্গটোৰ বাহুৰ দীঘ = 7 চে.মি.
∴ বৰ্গটোৰ কালি = (7 চে.মি.)² = 49 বর্গ চে.মি.।
(b) কোনটোৰ কালি বেছি হ’ব আৰু কিমান বেছি?
উত্তৰঃ বৰ্গটোৰ কালি = 49 বৰ্গ চে.মি.
বৰ্গটোৰ কালি = 62.36 বর্গ চে.মি.
∴ 62.36 বর্গ চে.মি. > 49 বর্গ চে.মি.
∴ বৃত্তটোৰ কালি বৰ্গৰ কালিতকৈ বেছি হ’ব।
এতিয়া, বৃত্তৰ কালি – বৰ্গৰ কালি = 62.36 – 49
= 1.36
∴ বৃত্তৰ কালি বৰ্গৰ কালিতকৈ 13.36 বর্গ চে.মি. বেছি হ’ব।
7. তলৰ চিত্ৰবোৰৰ আঁচটনা অংশৰ কালি উলিওৱা।
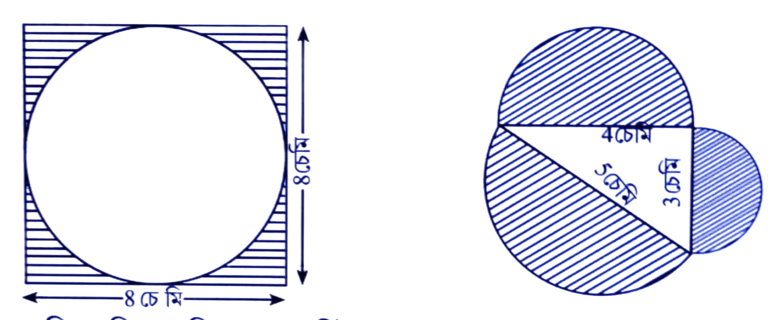
উত্তৰঃ চিত্ৰত বৰ্গৰ বাহুৰ দীঘ = 8 চে.মি.
বৃত্তৰ ব্যাস = 8 চে.মি.
∴ বৃত্তটোৰ ব্যাসার্ধ = 8/2 চে.মি. = 4 চে.মি.
∴ আঁচটনা অংশৰ কালি = বৰ্গৰ কালি – বৃত্তৰ কালি
= (8 চে.মি.)² {π(4 চে.মি.)²}
= 64 বর্গ চে.মি. – {22/7 × 4 × 4} বর্গ চে.মি.
= 64 বর্গ চে.মি. – 50.2857 বর্গ চে.মি.
= (64 – 50.29) বর্গ চে.মি. (প্রায়)
= 14.29 বর্গ চে.মি.
চিত্ৰত, প্ৰথম অর্ধবৃত্তৰ ব্যাস = 5 চে.মি.
∴ প্ৰথম অর্ধবৃত্তৰ ব্যাসার্ধ (r₁) = 5/2 চে.মি.
2য় অর্ধবৃত্তৰ ব্যাস = 4 চে.মি.
∴ 2 অর্ধবৃত্তৰ ব্যাসার্ধ (r₂) = 4/2 = 2 চে.মি.
3য় অর্ধবৃত্তৰ ব্যাস = 3 চে.মি.
∴ 3য় অর্ধবৃত্তৰ ব্যাসার্ধ (r₃) = 3/2 চে.মি.
∴ আঁচটনা অংশৰ কালি = প্রথম অর্ধবৃত্তৰ কালি + 2য় অর্ধবৃত্তৰ কালি + 3য় অর্ধবৃত্তৰ কালি
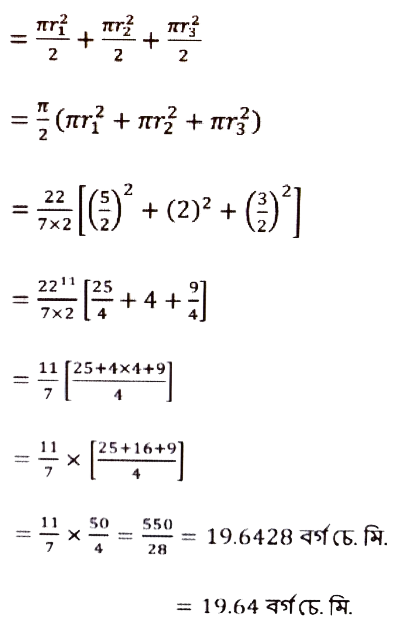
∴ আঁচটলা অংশৰ কালি = 19.64 বর্গ চে.মি.
8. এখন বৃত্তাকৃতিৰ ফুলনিৰ বাহিৰৰ চাৰিওফালে 1 মিটাৰ বহলৰ ৰাস্তা এটা আছে। ফুলনিখনৰ ব্যাস 66 মিটাৰ। ৰাস্তাটোৰ কালি নিৰ্ণয় কৰা। (π = 3.14)
উত্তৰঃ দিয়া আছে,
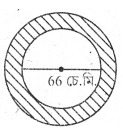
বৃত্তকাৰ ফুললিখনৰ ব্যাস = 66 চে.মি.
∴ বৃত্তকাৰ ফুলনিখনৰ ব্যাসার্ধ (r₁) = 66/2 = 33 চে.মি.
আকৌ, ৰাস্তাটোৰ সৈতে ফুললিখনৰ ব্যাস = (66 + 1 + 1) চে.মি.
= 68 চে.মি.
∴ ৰাস্তাটোৰ সৈতে ফুলনিখনৰ ব্যাসার্ধ (r₂) = 68/2 = 34 চে.মি.
9. এটা বৃত্তৰ পৰিধি 31.4 চে.মি.। বৃত্তটোৰ ব্যাসার্ধ আৰু কালি নিৰ্ণয় কৰা। (π = 3.14)
উত্তৰঃ দিয়া আছে, বৃত্তটোৰ পৰিধি = 31.4 চে.মি.
∴ 2πr = 31.4 (r, বৃত্তটোৰ ব্যাসার্ধ)
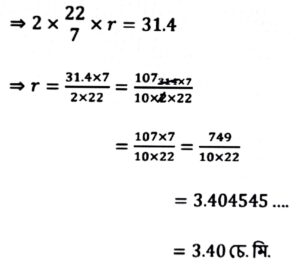
∴ বৃত্তটোৰ ব্যাসার্ধ (r) = 3.40 চে.মি.
∴ বৃত্তটোৰ কালি = πr² = 22/7 × (3.40 চে.মি.)²
= 22/7 × 11.56 = 36.331428 ……. = 36.33 বর্গ চে.মি.
10. 6 চে.মি. বাহুৰ বর্গাকৃতি এলুমিনিয়ামৰ পাত এখিলাৰ পৰা 2 চে.মি. ব্যাসার্ধৰ বৃত্ত এটা কাটি উলিয়াই দিয়া হ’ল। ৰৈ যোৱা এলুমনিয়াম পাতখিলাৰ কালি কিমান হ’ব? (π = 3.14)
উত্তৰঃ দিয়া আছে, বর্গাকৃতিৰ এলুমিনিয়ামৰ পাতখিলাৰ বাহুৰ দীঘ = 6 চে.মি.
∴ বর্গাকৃতিৰ পাতখিলাৰ কালি = (6 চে.মি.)²
(36) চে.মি.²
কাটি উলিওৱা বৃত্তটোৰ ব্যাসার্ধ = 2 চে.মি.
∴ বৃত্তটোৰ কালি = πr²
= 22/7 (2 চে.মি.)² = 22/7 × 4 চে. মি.² = 12.57142 ……
= 12.57 চে.মি.² (প্রায়)
∴ ৰৈ যোৱা এলুমিনিয়াম পাতখিলাৰ কালি = বৰ্গৰ কালি – বৃত্তৰ কালি
= 36 চে.মি.² – 12.57 চে.মি.²
= 23.43 চে.মি.²
11. 21 চে.মি. ব্যাসৰ অর্ধবৃত্ত এটাৰ পৰিধি আৰু কালি নিৰ্ণয় কৰা। (π = 22/7)
উত্তৰঃ দিয়া আছে, অর্ধবৃত্তৰ ব্যাস = 21 চে.মি.
অর্ধবৃত্তৰ ব্যাসার্ধ (r) = 21/2 চে.মি.
∴ অর্ধবৃত্তৰ পৰিধি = 2πr/2
= πr = 22/7 × 21/2
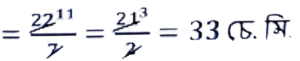
আকৌ, অর্ধবৃত্তটোৰ কালি = πr²
= 22/7 (21/2)² বর্গ চে.মি.
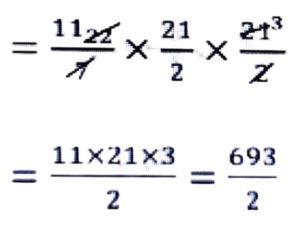
= 346.5 বৰ্গ চে.মি.
12. বৃত্তাকৃতিৰ কাঁহী এখনৰ কালি 38.5 বৰ্গ চে.মি.। কাঁহীখনৰ পৰিধি কিমান হ’ব? (π = 22/7)
উত্তৰঃ দিয়া আছে, বৃত্তাকৃতি কাঁহীখনৰ কালি = 38.5 বর্গ চে.মি.
∴ πr² = 38.5 য’ত r = বৃত্তৰ ব্যাসার্থ
⇒ 22/7r² = 385/10 ⇒ r² = (365 × 7)/(10 × 22)
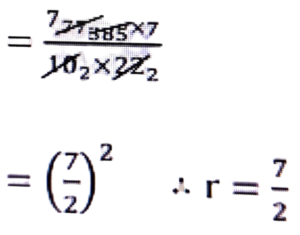
∴ বৃত্তৰ ব্যাসার্ধ = 3.5 চে.মি.
∴ বৃত্তৰ পৰিধি =πr
= (2 × 22/7 × 3.5
= 2 × 22 × 35⁵)/(7 × 10₂) = 22 চে.মি.
∴ কাঁহীখনৰ পৰিধি = 22 চে.মি.
13. 30 মিটাৰ বাহু বিশিষ্ট বর্গাকৃতিৰ বাগিচা এখনৰ সীমাৰ ভিতৰেদি 1 মিটাৰ প্ৰস্থৰ ৰাস্তা বন্ধা হৈছে। ৰাস্তাটোৰ কালি নিৰ্ণয় কৰা।
উত্তৰঃ দিয়া আছে, বর্গাকাৰ বাগিচাখনৰ বাহুৰ দীঘ = 30 মিটাৰ
∴ বাগিচাখনৰ ৰাস্তা বাদ দি বাহুৰ দীঘ = 30 – 1 – 1
= 28 মিটাৰ
∴ ৰাস্তাটোৰ কালি = (30 মিটাৰ)² – (28 মিটাৰ)²
= 900 মিটাৰ² – 784 মিটাৰ²
= 116 মিটাৰ²
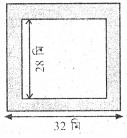
14. 30 মিটাৰ বাহু বিশিষ্ট বর্গাকৃতিৰ বাগিচা এখনৰ সোঁমাজেৰে 1 মিটাৰ বহলৰ দুটা পদপথ লম্বভাৱে কটাকৈ নির্মাণ কৰা হৈছে।
(i) পদপথৰ কালি নিৰ্ণয় কৰা।
উত্তৰঃ থিয়কৈ পদপথৰ দৈর্ঘ্য = 30 মি.
প্রস্থ = 1 মি.
আকৌ, পথালিকৈ পদপথৰ দৈর্ঘ্য = 1 মি.
প্রস্থ = 30 মি.
∴ পদপথৰ কালি = [{(30 × 1) + (1 × 30) – (1 × 1)}] বর্গ মি.
= (30 + 30 – 1) বর্গ মি.
= (60 – 1) বর্গ মি. = 59 বর্গ মি.
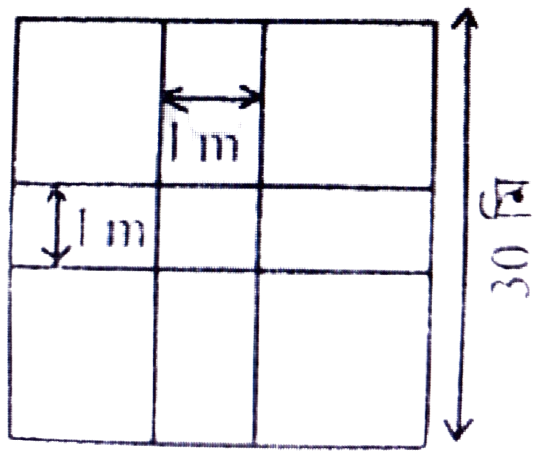
(ii) বাকী অংশৰ প্ৰতি বর্গ মিটাৰত কার্পেট ঘাঁহ লগাবলৈ 40 টকাকৈ খৰচ হ’লে মুঠ খৰচ কিমান হ’ব?
উত্তৰঃ দিয়া আছে, বর্গাকাৰ বাগিদাখনৰ বাহু = 30 মিটাৰ
∴ পদসখৰ বহল = 1 মিটাৰ
∴ পদপথ বাদ দি বাগিছাৰ কালি
= [(30 × 30) – {(30 × 1) + (1 × 30)} – 1) × 1] বর্গ মিটাৰ
= 900 – {30 + 30 – 1}
= 900 – (60 – 1) = 841 বর্গ মিটাৰ।
প্রতি বর্গমিটাৰ কার্পেট ঘাঁহ লগোৱা খৰছ = 40 টকা
∴ ঘাঁহ লগোৱা মুঠ খৰচ = 841 × 40 টকা
= 33640 টকা।
15. এখন 125 মি দৈর্ঘ্য আৰু 65 মি প্রস্থৰ আয়তাকৃতিৰ উদ্যানৰ বাহিৰৰ চাৰিওফালে 3 মি বহলৰ ৰাস্তা আছে। এই ৰাস্তাটোৰ কালি উলিওৱা।
উত্তৰঃ দিয়া আছে, আয়তাকাৰ উদ্যানখনৰ দীঘ = 125 মি.
প্রস্থ = 65 মি.
আকৌ ৰাস্তাৰ সৈতে উদ্যানখনৰ প্ৰস্থ = (125 + 3 + 3) মি.
= 131 মি.
আৰু ৰাস্তাৰ সৈতে উদ্যানখনৰ প্ৰস্থ = (65 + 3 + 3) মি.
= 71 মি.
∴ ৰাস্তাটোৰ কালি = ৰাস্তাৰ সৈতে বাগিছাৰ কালি – উদ্যানখনৰ কালি
= (131 × 71) বর্গ মি. – (125 × 65) বর্গ মি.
= (9310 – 8125) বর্গ মি.
= 1176 বর্গ মি.
16. 10 মিটাৰ দৈৰ্ঘ্যৰ আৰু 5 মিটাৰ প্ৰন্থৰ আয়তাকৃতিৰ পাত এখিলাৰ পৰা 2 মিটাৰ ব্যাসার্ধৰ বৃত্ত দুটা কাটি পেলাই দিয়া হ’ল। আয়তাকৃতিৰ পাতখিলাৰ ৰৈ যোৱা অংশৰ কালি কিমান হ’ব?
উত্তৰঃ আয়তকাৰ পাতখিলাৰ দীঘ = 10 মি.
প্রস্থ = 5 মি.
∴ পাতখিলাৰ কালি = দীঘ × প্রস্থ
= (10 × 5) বর্গ মি. = 50 বর্গ মি.
আকৌ, কাটি পেলোৱা বৃত্তৰ ব্যাসার্ধ = 2 মি.
∴ বৃত্তৰ ব্যাসার্ধ = πr² = 22/7 × 2 × 2 বর্গ মি. = 12.571 বর্গ মি.
∴ পাতখিলাৰ ৰৈ যোৱা অংশৰ কালি = 50 – 12.571 বর্গ মি.
= 37.429 বর্গ মি.
17. এটা 5.5 মিটাৰ দীঘল আৰু 4 মিটাৰ বহল কোঠাৰ চাৰিওফালে সংলগ্ন কৰি 2.25 মিটাৰ বহল এখন বাৰাণ্ডা বনোৱা হ’ল।
(i) বাৰাণ্ডাৰ কালি উলিওৱা।
(ii) প্রতি বর্গ মিটাৰত 200 টকাকৈ খৰচ হ’লে বাৰাণ্ডাখনৰ মজিয়া পকী কৰোঁতে খৰচ কিমান হ’ব?
উত্তৰঃ দিয়া আছে,
কোঠাটোৰ দীঘ = 5.5 মি.
কোঠাটোৰ প্ৰস্থ = 4 মি.
∴ কোঠাটোৰ কালি = 5.5 × 4 বর্গ মি.
=22.0 বর্গ মি.
আকৌ, বাৰাণ্ডাৰ সৈতে কোঠাৰ দীঘ = (5.5 + 2.25 + 2.25) মি.
= 10. মি.
বাৰাণ্ডাৰ সৈতে কোঠাৰ প্ৰস্থ = (4 + 2.25 + 2.25) মি.
= 8.5 মি.
∴ বাৰাণ্ডাৰ সৈতে কোঠাৰ কালি = 10 × 8.5 বর্গ মি.
= 85.0 বর্গ মি.
(i) বাৰাণ্ডাৰ কালি = বাৰাণ্ডাৰ সৈতে কোঠাৰ কালি – কোঠাৰ কালি
= (85 – 22) বর্গ মি.
= 63 বর্গ মি.
(ii) 1 বর্গ মি. পকী কৰা খৰচ = 200 টকা।
∴ পকী কৰা মুঠ খৰচ = 200 × 63
= 12600 টকা।
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

