SEBA Class 7 Mathematics (Assamese Medium) Chapter 1 – অখণ্ড সংখ্যা Solutions & Summary
Find SEBA Class 7 Mathematics Chapter 1 – “অখণ্ড সংখ্যা” (Whole Numbers) solutions, designed for Assamese medium students. This chapter introduces the concept of whole numbers, their properties, and operations such as addition, subtraction, multiplication, and division.
Students will learn about successor and predecessor, number line representation, commutative, associative, and distributive properties, and the importance of zero and one in whole numbers. The chapter also covers patterns in whole numbers and the application of these concepts in real-life situations.
Our solutions include SCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students build a strong foundation in mathematics and excel in exams.
To access solutions for all chapters, Click Here
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীলনী – 1.1 |
|---|
1. 5 আৰু (-13) ৰ মাজত কিমানটা অখণ্ড সংখ্যা আছে?
উত্তৰঃ 5 আৰু (-13) ৰ মাজত 17 টা অখণ্ড সংখ্যা আছে।
2. 13 আৰু (-13) ৰ মাজৰ আটাইতকৈ ডাঙৰ আৰু আটাইতকৈ সৰু অখণ্ড সংখ্যা দুটা লিখা।
উত্তৰঃ 13 আৰু (-13) ৰ মাজৰ আটাইতকৈ ডাঙৰ সংখ্যাটো 12 আৰু আটাইতকৈ সৰু সংখ্যাটো (-12)।
3. তলত দিয়া অখণ্ড সংখ্যাবোৰ সংখ্যাৰেখাত বহুওৱা–
-6, 4, -10, 5, -1
উত্তৰঃ

4. -15 তকৈ ডাঙৰ 5 টা ঋণাত্মক অখণ্ড সংখ্যা লিখা।
উত্তৰঃ -15 তকৈ ডাঙৰ 5 টা ঋণাত্মক অখণ্ড সংখ্যাসমূহ হ’ল– 13, -12, -9, -8, -2
5. সত্য নে অসত্য কোৱা।
(i) ধনাত্মক অখণ্ড সংখ্যাবোৰক স্বাভাৱিক সংখ্যা বুলি কোৱা হয়।
উত্তৰঃ সত্য।
(ii) আটাইবোৰ অখণ্ড সংখ্যাই পূর্ণ সংখ্যা।
উত্তৰঃ অসত্য।
(iii) সংখ্যাৰেখাডাল ‘0’ (শূন্য) ৰ দুয়োফালে অসীমলৈ বিস্তাৰিত।
উত্তৰঃ সত্য।
(iv) ‘0’ আৰু ঋণাত্মক অখণ্ড সংখ্যাবোৰেৰে পূৰ্ণ সংখ্যাৰ থূপটো গঠিত।
উত্তৰঃ অসত্য।
(v) যদি a + b = 0, তেন্তে ইহঁতৰ এটা আনটোৰ যোগাত্মক বিপৰীত।
উত্তৰঃ সত্য।
6. এযোৰ অখণ্ড সংখ্যা লিখা যাৰ–
(i) যোগফল -3
উত্তৰঃ -8 আৰু 5 ৰ যোগফল = (-8) + 5 = -3
∴ এযোৰ অখণ্ড সংখ্যা যাৰ যোগফল -3 হ’ল -৪ আৰু 5
(ii) বিয়োগফল -5
উত্তৰঃ -10 আৰু -5 ৰ বিয়োগফল = 10 – (-5)
= -10 + 5 = -5
∴ এযোৰ অখণ্ড সংখ্যা যাৰ যোগফল -5 হ’ল -10 আৰু -5
(iii) যোগফল 0
উত্তৰঃ 100 আৰু -100 ৰ যোগফল = 100 + (-100)
= 100 – 100 = 0
∴ এযোৰ অখণ্ড সংখ্যা যাৰ যোগফল 0 হ’ল -100 আৰু -100
(iv) বিয়োগফল 2
উত্তৰঃ 9 আৰু 7 ৰ বিয়োগফল = 9 – 7 = 2
∴ এযোৰ অখণ্ড সংখ্যা যাৰ যোগফল 2 হ’ল 9 আৰু 7
(বিঃদ্রঃ এনে অখণ্ড সংখ্যাৰ বাবে যিকোনো অখণ্ড সংখ্যা লৈ পাব পাৰি।)
7. এযোৰ ঋণাত্মক অখণ্ড সংখ্যা লিখা যাব বিয়োগফল 6।
উত্তৰঃ -11 আৰু -17 বিয়োগফল = -11 – (-17)
= -11 + 17
= 6
∴ এযোৰ ঋণাত্মক অখণ্ড সংখ্যা যাৰ বিযোগফল 6 হ’ল -11 আৰু -17
৪. অখণ্ড সংখ্যা a আৰু b নিৰ্ণয় কৰা যাতে–
(i) a + b ধনাত্মক।
উত্তৰঃ a + b ধনাত্মক
ধৰা হ’ল, a = 5, b = 3
∴ a + b = 5 + 3 = 8 ধনাত্মক।
(ii) a ≠ b
উত্তৰঃ a ≠ b
a = 5, b = -2 লৈ পাওঁ,
a ≠ b
(iii) a – b = 0
উত্তৰঃ a – b = 0
a = 9 আৰু b = 9 লৈ পাওঁ,
a – b = 9 – 9 = 0
অৰ্থাৎ, a – b ৰ বাবে a – b = 0 হ’ব।
9. বাকচৰ ভিতৰৰ খালী ঠাই পূৰ কৰা–
(i) (-15) + (-4) = (-4) + ……।
উত্তৰঃ (-15) + (-4) = (-4) + -15
(ii) ……. + {(-7) + 8} = {5 + (-7)} + 8
উত্তৰঃ 8 + {(-7) + 8} = {5 + (-7)} + 8
(iii) (-23) + ……. = -23 = (-23) + …….।
উত্তৰঃ (-23) + 0 = -23 = (-23) + 0
(iv) (-19) + …… = (-27)
উত্তৰঃ (-19) + -8 = (-27)
(v) x + 12 = 0 হ’লে x = ……।
উত্তৰঃ x + 12 = 0 হ’লে x = -12
10. এজন মানুহে A স্থানৰ পৰা 14 কিলোমিটাৰ পূবে গ’ল। কিন্তু আন এজন মানুহে A স্থানৰ পৰা 6 কিলোমিটাৰ পশ্চিমে গ’ল। তেতিয়া তেওঁলোকৰ দূৰত্বৰ অন্তৰ কি হ’ব?
উত্তৰঃ A স্থানৰ পৰা পূবলৈ যোৱা দূৰত্ব = 14 কি.মি.
A স্থানৰ পৰা পশ্চিমলৈ যোৱা দূৰত্ব = -6 কি.মি.
∴ তেওঁলোকৰ দূৰত্বৰ অন্তৰ = 14 (-6) কি.মি.
= 14 + 6 = 20 কি.মি.
11. এজন মানুহৰ হাতত 35 টকা জমা আছে কিন্তু আন এজনৰ 40 টকা ধাৰ আছে। প্রথমজন মানুহ দ্বিতীয়জন মানুহতকৈ কিমান চহকী?
উত্তৰঃ প্রথম মানুহজনৰ হাতত জমা আছে = 35 টকা
আনজন মানুহৰ ধাৰ আছে = 40 টকা
∴ প্রথমজন দ্বিতীয়জনকৈ চহকী হ’ব = 35 – (40) টকা
= (35 + 40) = 75 টকা।
12. কোনো এটা মঙলবাৰে পুৱা 5 বজাত গুৱাহাটীত তাপমাত্রা আছিল 25°C। কিন্তু বিয়লি 2 বজাত তাপমাত্রা ৪°C বাঢ়িল আৰু ৰাতি 10 বজাত 3°C কমি তাপমাত্রা কমিল। বুধবাৰে দুপৰীয়া 12 বজাৰ পিছত তাপমাত্রা পুনৰ 5°C বাঢ়িলে। এই সময়ত তাপমাত্রা কিমান হ’ল?
উত্তৰঃ মঙলবাৰে গুৱাহাটীৰ তাপমাত্রা (5 বজাত) 25°C
বিয়লি 2 বজাত তাপমাত্রা ৪°C
ৰাতি 10 বজাত কমে 3°C
বুধবাৰে তাপমাত্রা বাঢ়ে 5°C
∴ বুধবাৰে 12 বজাৰ পিছত তাপমাত্ৰা হ’ব = 25°C + 8°C – 3°C + 5°C
= 25°C + 8°C + 5°C + 3°C
= 35°C
13. অনুৰাধাই বেংকত 3,200 টকা জমা থলে আৰু পিছদিনা তাৰে 2,540 টকা উলিয়াই আনিলে। টকাখিনি উলিয়াই অনাৰ পিছত বেংকত অনুৰাধাৰ কিমান টকা জমা থাকিব?
উত্তৰঃ অনুৰাধাই বেংকত জমা থলে = 3200 টকা
পিছদিনা উলিয়াই আনিলে = 2540 টকা
∴ বেংকত অনুৰাধাৰ জমা থাকিব = 3200 টকা – 2540 টকা
= 660 টকা।
14. দুটা সংখ্যাৰ যোগফল -5। যদি এটা সংখ্যা 18 হয় আনটো সংখ্যা কিমান হ’ব?
উত্তৰঃ সংখ্যা দুটাৰ যোগফল = -5
এটা সংখ্যা = 18
∴ আনটো সংখ্যা = -5 – (18)
= -5 – 18 = -23
15. -23ৰ লগত কি যোগ কৰিলে যোগফল 0 হ’ব?
উত্তৰঃ -23 ৰ লগত 23 যোগ কৰিলে যোগফল 0 হ’ব।
16. দুটা অখণ্ড সংখ্যাৰ যোগফল -48। তাৰে এটা -20 হ’লে আনটো কিমান হ’ব?
উত্তৰঃ অখণ্ড সংখ্যা দুটাৰ যোগফল = -48
এটা সংখ্যা = -20
∴ আনটো সংখ্যা = -48 – (-20)
= -48 + 20 = -28
17. সংখ্যাৰেখা ব্যৱহাৰ কৰি মান নির্ণয় কৰা।
(i) (+5) – (+3)
উত্তৰঃ (+5) – (+3)
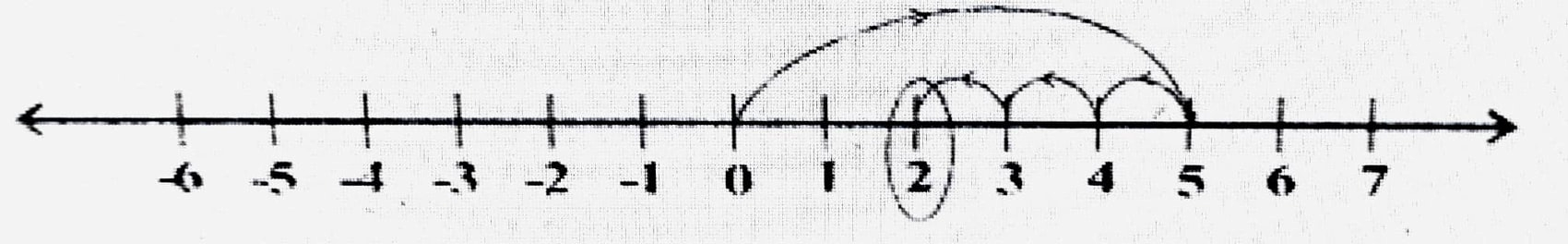
(ii) (+6) + (-5)
উত্তৰঃ (+6) + (-5)

(iii) (-6) – (+5)
উত্তৰঃ (-6) – (+5)

(iv) (-8) + (-3)
উত্তৰঃ (-8) + (-3)

18. তলৰ উক্তিসমূহৰ শুদ্ধ অশুদ্ধ বিচাৰ কৰা।
(i) (-6) + 23 + (-2) = (-2) + (-6) + 23
উত্তৰঃ শুদ্ধ।
(ii) (16 -15) + (-7) = 16 – {15 + (-7)}
উত্তৰঃ অশুদ্ধ।
(iii) স্বাভাৱিক সংখ্যা সমূহ বিয়োগত আৱদ্ধ।
উত্তৰঃ অশুদ্ধ।
(iv) 0 আৰু -670 ৰ ভিতৰত -670 সংখ্যাটো ডাঙৰ।
উত্তৰঃ অশুদ্ধ।
(v) বিয়োগত ক্রম বিনিময় আৰু সহযোেগ ধর্ম প্রযোজ্য নহয়।
উত্তৰঃ শুদ্ধ।
অনুশীলনী – 1.2 |
|---|
1. পূৰণফল নিৰ্ণয় কৰা–
(i) 5 × (- 2)
উত্তৰঃ 5 × (- 2)
= -(5 × 2)
= -10
(ii) (- 3) × 7
উত্তৰঃ (- 3) × 7
= -(3 × 7)
= -21
(iii) (-4) × (-3)
উত্তৰঃ (-4) × (-3)
= 4 × 3
= 12
(iv) (-129) × (-1)
উত্তৰঃ (-129) × (-1)
= (129 × 1)
= 129
(v) (-12) × 0 × (-17)
উত্তৰঃ (-12) × 0 × (-17)
= (12 × 17) × 0
= 0
(vi) (-22) × (-11) × 10
উত্তৰঃ (-22) × (-11) × 10
= (22 × 11) × 10
= 242 × 10
= 2420
(vii) 13 × (-5) × (-3)
উত্তৰঃ 13 × (-5) × (-3)
= 13 × 5 × 3
= 195
(viii) (-27) × (-31) × (-2)
উত্তৰঃ (-27) × (-31) × (-2)
= -(27 × 31 × 2)
= -1674
(ix) (-3) × (-1) × (-2) × 5
উত্তৰঃ (-3) × (-1) × (-2) × 5
= -(3 × 1 × 2 × 5)
= -30
2. সত্যাসত্য বিচাৰ কৰা–
(i) 27 × {(-5) + 10} = 27 × (-5) + 27 × 10
উত্তৰঃ 27 × {(-5) + 10} = 27 × (-5) + 27 × 10
⇒ 27 × (-5 + 10) = 27(-5 + 10)
⇒ 27 × 5 = 27 × 5
∴ বাওঁপক্ষ = সোঁপক্ষ
(ii) (-25) × {(-16) + (-24)} = (-25) × (-16) × (-24)
উত্তৰঃ ⇒ (25) × (-16 – 24) = { – (25 × 16 × 24)}
⇒ (25) × (-40) = -(9600)
∴ বাওঁপক্ষ = সোঁপক্ষ
(iii) a – b = a + b, য’ত a = (-75), b = (-20)
উত্তৰঃ বাওঁপক্ষ = a – (-b)
= a + b
= (75) + (-20)
= -75 – 20 = -(75 + 20) = -95
সোঁপক্ষ = a + b = (-75) + (-20)
= -(75 + 20) = -95
∴ বাওঁপক্ষ = সোঁপক্ষ
3. (i) যিকোনো দুটা অখণ্ড সংখ্যাৰ পূৰণফল -33। তাৰে এটা 11 হ’লে আনটো কিমান?
উত্তৰঃ অখণ্ড সংখ্যাৰ দুটাৰ পূৰণফল = -33
সংখ্যা দুটাৰ এটা = 11
∴ আনটো সংখ্যা হ’ব = (-33) ÷ 11
= -33/11 = -3
(ii) যিকোনো দুটা অখণ্ড সংখ্যাৰ পূৰণফল 51। তাৰে এটা -1 হ’লে আনটো কিমান?
উত্তৰঃ অখণ্ড সংখ্যাৰ দুটাৰ পূৰণফল = 51
সংখ্যা দুটাৰ এটা = -1
∴ আনটো সংখ্যা হ’ব = 51 ÷ -1
= 51/-1 = -51
(iii) যিকোনো অখণ্ড সংখ্যা a ৰ বাবে (-1 × a) ৰ মান কিমান হ’ব?
উত্তৰঃ A এটা যিকোনো অখণ্ড সংখ্যা
∴ -1 × a = -a
4. উপযুক্ত বিধি প্রয়োগ কৰি পূৰণফল নির্ণয় কৰা–
(i) 125 × (-54) × 8
উত্তৰঃ 125 × (-54) × 8
= (125 × 8) × (-54) (ক্রম বিনিময় বিধি)
= 1000 × (-54)
= -54000
(ii) (-25) × (-97) × 4
উত্তৰঃ (-25) × (-97) × 4
= (-25 × 4) × (-97) (ক্রম বিনিময় বিধি)
= -100 × (-97)
= 9700
(iii) (-27) × (-33)
উত্তৰঃ (-27) × (-33)
= (27 × 33)
= (30 – 3) × (30 + 3)
= 300(30 + 3) – 3(30 + 3) (বিতৰণ বিধি)
= 900 + 90 – 90 – 9
= 900 – 9
= 891
(iv) 25 × (-58) + (-58) × (-35)
উত্তৰঃ 25 × (-58) + (-58) × (-35)
= -58{25 + (-35)} (বিতৰণ বিধি)
= -58(25 – 35)
= -58 × (-10)
= 580
(v) 15 × (-25) × (-4) × (-10)
উত্তৰঃ 15 × (-25) × (-4) × (-10)
= {(-25) × (-4)} × {15 × (-10)} (ক্রম বিনিময় বিধি)
= 100 × (-150)
= -15000
(vi) (-57) × (-19) × 57
উত্তৰঃ (-57) × (-19) × 57
= 57 × 19 × 57
= 57 × 19
= 57 × (20 – 1)
= 57 × 20 – 57 × 1
= 1140 – 57
= 1083
5. বিনিময় আৰু সহযোগ বিধিৰ সহায়ত মান নির্ণয় কৰাঃ
(i) 125 × (54) × 8
উত্তৰঃ 125 × (54) × 8
= 125 × 8 × 54 (ক্রমবিনিময় বিধি)
= (100 + 25) × 8 × (54) (সহযোগ বিধি)
= (800 + 200) × (54)
= 1000 × 54
= 54000
(ii) (-25) × 75 × 8 × (-4)
উত্তৰঃ (-25) × 75 × 8 × (-4)
= (-25) × (-4) × 75 × 8 (ক্রমবিনিময় বিধি)
= 100 × 600
= 60,000
(iii) 225 × 67 × 3
উত্তৰঃ 225 × 67 × 3
= 225 × 3 × 67 (ক্রমবিনিময় বিধি)
= 225 × 3 × (70 – 3) (সহযোেগ বিধি)
= 675 × (70 – 3)
= 675 × 70 – 675 × 3
= 47250 – 2025 = 45225
6. বিতৰণ বিধিৰ সহায়ত মান নির্ণয় কৰাঃ
(i) 172 × 25 + 172 × 35
উত্তৰঃ 172 × 25 + 172 × 35
= 172(25 + 35)
= 172(60)
= 10320
(ii) 159 × 82 + 159 × 16 + 159 × 2
উত্তৰঃ 159 × 82 + 159 × 16 + 159 × 2
= 159(82 + 16 + 2)
= 159(100)
= 15900
(iii) 67 × 78 + 67 × (-43) + 67 × (-25)
উত্তৰঃ 67 × 78 + 67 × (-43) + 67 × (-25)
= 67{(78 + (-43) + (-25)}
= 67(78 – 43 – 25)
= 67 × (78 – 68)
= 67 × 10
= 670
(iv) 999 × 99 + 99
উত্তৰঃ 999 × 99 + 99
= 99(999 + 1)
= 99 × 1000
= 99000
(v) 58 × 47 + 94
উত্তৰঃ 58 × 47 + 94
= 58 × 47 + 47 × 2
= 47(58 + 2)
= 47 × 60
= 2,820
7. শুদ্ধ অশুদ্ধ বিচাৰ কৰাঃ
(i) (-7) × 15 × (-4) = (-7) × 15 + (-7) × (-4)
উত্তৰঃ (-7) × 15 × (-4) = (-7) × 15 + (-7) × (-4)
⇒ 28 × 15 = (-7){15 + (-4)}
⇒ 28 × (20 – 5) = (-7) × (15 – 4)
⇒ 28 × 20 – 28 × 5 = (-7) × (15 – 4)
⇒ 560 – 140 = (-7) × 11
⇒ 420 = -77
∴ অশুদ্ধ।
(ii) (-6) × 23 × (-2) = (-2) × (-6) × 23
উত্তৰঃ (-6) × 23 × (-2) = (-2) × (-6) × 23
= (-6) × 23 × (-2), শুদ্ধ।
(iii) (-5) × {(-3) × 2) = {(-5) × (-3)} x 2
উত্তৰঃ (-5) × {(-3) × 2) = {(-5) × (-3)} × 2
= (-5) × {(-3) × 2}, শুদ্ধ।
(iv) (-175) × (-1) = -175
উত্তৰঃ (-175) × (-1) = -175
⇒ 175 = -175 অশুদ্ধ।
(v) (-25) × (-4) × 0 = 100
উত্তৰঃ (-25) × (-4) × 0 = 100
⇒ 100 × 0 = 100
⇒ 0 = 100 অশুদ্ধ।
অনুশীলনী – 1.3 |
|---|
1. হৰণফল নিৰ্ণয় কৰা–
(i) 14 ÷ (-5)
উত্তৰঃ 14 ÷ (-5)
= 14/-5
= -2.8
(ii) (-60) ÷ 10
উত্তৰঃ (-60) ÷ 10
= -6
(iii) (-54) ÷ (-6)
উত্তৰঃ (-54) ÷ (-6)
= 9
(iv) 0 ÷ (-15)
উত্তৰঃ 0 ÷ (-15)
= 0
(v) (-61) ÷ {(-60) + (-1)}
উত্তৰঃ (-61) ÷ {(-60) + (-1)}
= (-61) ÷ (-61)
= 1
(vi) {(-72) ÷ (-6)} ÷ (-3)
উত্তৰঃ {(-72) ÷ (-6)} ÷ (-3)
= 12 ÷ (-3)
= -4
2. খালী ঠাই পূৰ কৰা–
(i) (-600) ÷ 25 = ____________
উত্তৰঃ (-600) ÷ 25 = -24
(ii) {(-4) × 18} ÷ ____________ = 12
উত্তৰঃ {(-4) × 18} ÷ -6 = 12
(iii) _____________ ÷ (5 – 6) = -20
উত্তৰঃ 20 ÷ (5 – 6) = -20
(iv) (-123) ÷ (-1) = _____________
উত্তৰঃ (-123) ÷ (-1) = 123
3. (i) যদি a ÷ (-7) = 8, তেন্তে অখণ্ড সংখ্যা a ৰ মান নির্ণয় কৰা।
উত্তৰঃ a ÷ (-7) = 8
⇒ a/-7 = 8
⇒ a = -56
(ii) যদি 125 ÷ b = -5, তেন্তে অখণ্ড সংখ্যা b ৰ মান নির্ণয় কৰা।
উত্তৰঃ 125 ÷ b = -5
⇒ 125/b = 5
⇒ b = 125/-5 = -25
4. a ÷ b = -5 হোৱাকৈ তিনিযোৰ অখণ্ড সংখ্যা লিখা।
উত্তৰঃ (i) 15 ÷ (-3) = -5
(ii) (-20) ÷ 4 = -5
(iii) 60 ÷ (-12) = -5
∴ নির্ণেয় অখণ্ড সংখ্যা তিনিযোৰ হ’ল 15, (-3); -20, 4; 60, (-12)
5. শ্রেণী পৰীক্ষা এটাত 20 টা প্রশ্ন দিয়া হৈছে। প্ৰতিটো শুদ্ধ উত্তৰৰ বাবে 5 নম্বৰ আৰু প্ৰতিটো ভুল উত্তৰৰ বাবে (-2) নম্বৰ দিয়া হৈছে।
(i) এজনে সকলো প্ৰশ্নৰ উত্তৰ কৰিলে। কিন্তু তাইৰ 10 টাহে শুদ্ধ হৈছিল। তেওঁৰ পোৱা মুঠ নম্বৰ কিমান?
উত্তৰঃ 1 টা শুদ্ধ উত্তৰৰ বাবে নম্বৰ পায় = 5
∴ 10 টা শুদ্ধ উত্তৰৰ বাবে নম্বৰ পায় = 5 × 10 = 50
1 টা অশুদ্ধ নম্বৰৰ বাবে নম্বৰ = -2
∴ 10 টা অশুদ্ধ নম্বৰৰ বাবে নম্বৰ = -2 × 10 = -20
∴ তেওঁ পোৱা মুঠ নম্বৰ = 50 + (-20) = 50 – 20 = 30
(ii) অন্য এজনে 5 টা শুদ্ধ কৰিলে। তেওঁৰ নম্বৰ কিমান হ’ব?
উত্তৰঃ আন এজনে পাঁচটা শুদ্ধ উত্তৰ কৰে
∴ পাঁচটা শুদ্ধ উত্তৰৰ বাবে নম্বৰ = 5 × 5 = 25
∴ 15 টা অশুদ্ধ উত্তৰৰ বাবে নম্বৰ = -2 × 15 = -30
∴ তেওঁ পোৱা নম্বৰ = 25 + (-30) = -5
6. এটা পৰীক্ষাত প্ৰতিটো শুদ্ধ উত্তৰৰ বাবে 5 নম্বৰ আৰু প্ৰতিটো অশুদ্ধ উত্তৰৰ বাবে (-2) নম্বৰ দিয়া হৈছিল।
(i) সুমনে প্ৰতিটো প্ৰশ্নৰ উত্তৰ কৰিছিল। তাৰে তেওঁৰ 16 টা শুদ্ধ হ’ল আৰু 64 নম্বৰ পালে।
উত্তৰঃ 1 টা শুদ্ধ উত্তৰৰ বাবে নম্বৰ = 5
1 এটা অশুদ্ধ উত্তৰৰ বাবে নম্বৰ = -2
∴ 16 টা শুদ্ধ উত্তৰৰ বাবে প্ৰাপ্ত নম্বৰ = 5 × 16 = 80
কিন্তু তেওঁৰ প্ৰাপ্ত নম্বৰ = 64
∴ ভুল উত্তৰৰ বাবে পোৱা নম্বৰ = 64 – 80 = -16
∴ সুমনৰ ভুল উত্তৰৰ নম্বৰ = -16 ÷ (-2) = ৪ টা
(ii) জয়াই আটাইকেইটা প্ৰশ্নৰ উত্তৰ কৰিছিল। তেওঁ 6 টা শুদ্ধ কৰিছিল আৰু (-6) নম্বৰ পালে। দুয়ো কেইটা প্ৰশ্নৰ উত্তৰ ভুল কৰিছিল?
উত্তৰঃ 1 টা শুদ্ধ উত্তৰৰ বাবে নম্বৰ = 5
1 টা অশুদ্ধ উত্তৰৰ বাবে নম্বৰ = -2
6 টা শুদ্ধ উত্তৰৰ বাবে নম্বৰ পায় = 6 × 5 = 30
কিন্তু জয়াৰ প্ৰাপ্ত নম্বৰৰ সংখ্যা = -6
∴ ভুল উত্তৰৰ বাবে পোৱা মুঠ নম্বৰ = (-6) – 30 = -36
∴ তেওঁৰ ভুল উত্তৰৰ সংখ্যা = (-36) ÷ (-2) = 18 টা
7. কোনো এটা ৰবৰ কোম্পানীয়ে বিক্ৰী কৰা প্ৰতিবেগ ৰবৰত 15 টকাকৈ লাভ কৰে। প্রতিবেগ বেয়া হৈ যোৱা ৰবৰত ৪ টকাকৈ লোকচান কৰে।
(i) কোম্পানীটোৱে এমাহত 1500 বেগ ভাল ৰবৰ আৰু 500 বেগ বেয়া ৰবৰ বিক্ৰী কৰিলে। ইয়াত লাভ বা লোকচান কিমান হ’ব?
উত্তৰঃ কোম্পানীটোৱে ভাল ৰবৰত লাভ কৰে = 15 টকা।
কোম্পানীটোৱে বেয়া ৰবৰত লোকচান কৰে = ৪ টকা।
(i) কোম্পানীটোৱে 1500 বেগ ভাল ৰবৰৰ বাবে লাভ কৰে = 15 × 1500 টকা
= 22500 টকা
কোম্পানীটোৱে 500 বেগ বেয়া ৰবৰৰ বাবে লোকচান কৰে = 8 × 500 টকা
= 4000 টকা
∴ লাভ > লোকচান
∴ কোম্পানীটোৰ মুঠ লাভ = (22500 – 4000)
= 18500 টকা
(ii) যদি 750 বেগ বেয়া ৰবৰ বিক্ৰী কৰা হয় তেন্তে কোনো লাভ বা লোকচান নহ’বলৈ মুঠ কিমান বেগ ভাল ৰবৰ বিক্ৰী কৰিব লাগিব?
উত্তৰঃ 750 বেগ বেয়া ৰবৰত লোকচান হ’ব = 750 × 8
= 6000 টকা
∴ লাভ বা লোকচান নহ’বলৈ লাভ হ’ব লাগিব = 6000 টকা
∴ কোম্পানীটোৱে ভাল ৰবৰ বিক্ৰী কৰা বেগৰ সংখ্যা = 6000 ÷ 15 = 400 বেগ
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

