SEBA Class 7 Mathematics (Assamese Medium) Chapter 10 – ব্যৱহাৰিক জ্যামিতি Solutions & Summary
Find SEBA Class 7 Mathematics Chapter 10 – “ব্যৱহাৰিক জ্যামিতি” (Practical Geometry) solutions, designed for Assamese medium students. This chapter explains various geometric constructions using a ruler and compass, including drawing triangles, perpendicular bisectors, and angle bisectors.
Students will learn about constructing different types of angles, triangles with given conditions, bisecting a line segment, and drawing parallel lines. The chapter also covers real-life applications of geometry in design, architecture, and engineering.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students master geometric constructions and perform well in exams.
To access solutions for all chapters, Click Here
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীলনী – 10.1 |
|---|
1. এডাল যিকোনো ৰেখা m আঁকা। m ৰ ওপৰত নথকা যিকোনো এটা বিন্দু A লোৱা। এতিয়া m ৰ সমান্তৰাল হোৱাকৈ A ৰ মাজেৰে যোৱাকৈ এডাল ৰেখা আঁকা।
উত্তৰঃ অংকন প্রণালীঃ m ৰ ওপৰত নথকা A যিকোনো এটা বিন্দু। A বিন্দৰে m ৰ সমান্তৰাল হোৱাকৈ এডাল ৰেখা অংকন কৰিব লাগে।
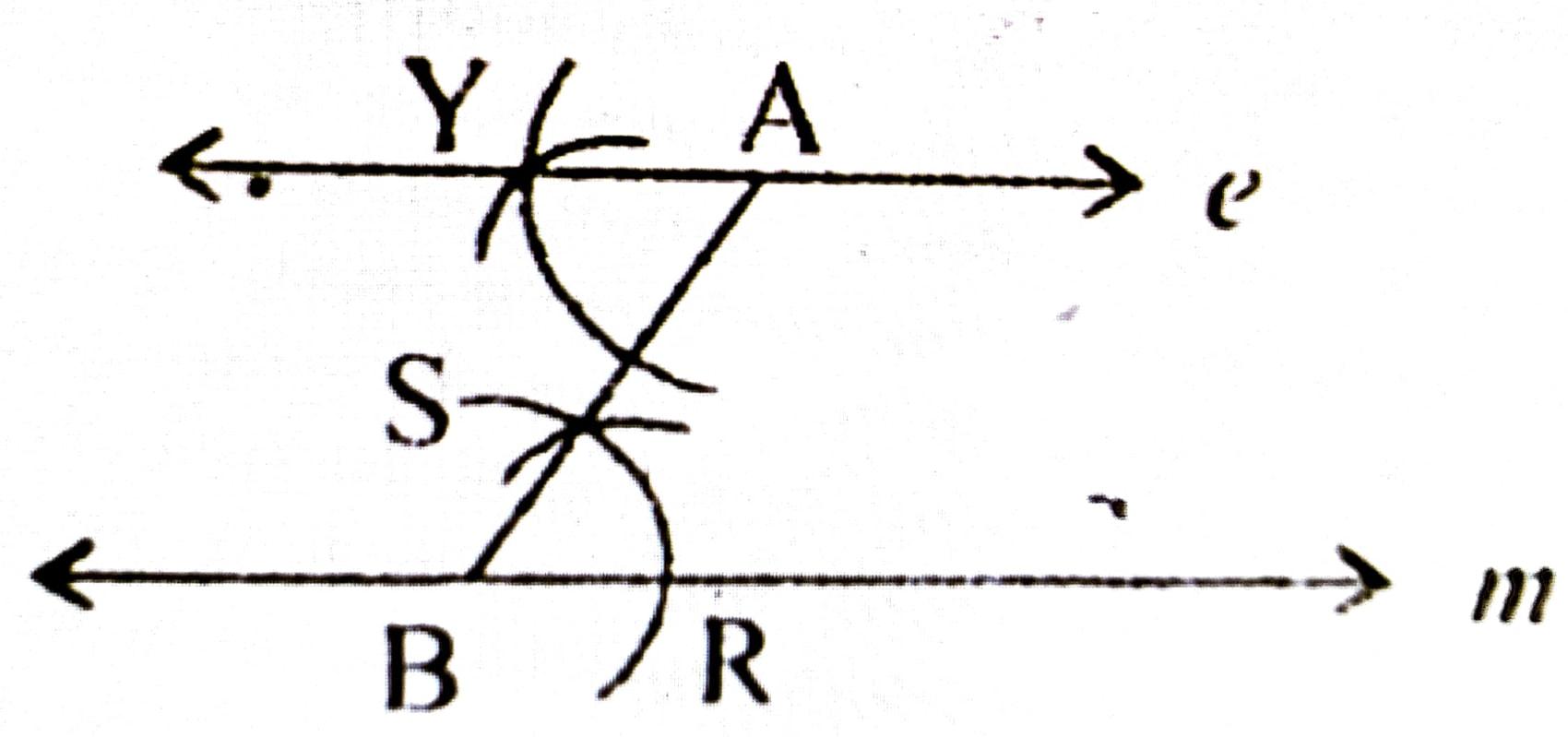
পৰ্যায় 1: m ৰ ওপৰত যিকোনো এটা বিন্দু B লোৱা হ’ল।
B, A সংযোগ কৰা হ’ল।
পর্যায় 2: B বিন্দু কেন্দ্ৰ কৰি AB আৰু M ক কটাকৈ যিকোনো ব্যাসার্দ্ধৰ এটা বৃত্তচাপ আঁকা হ’ল। এই চাপটোৱে AB আৰু M ক বিন্দু দুটাক ক্রমে S আৰু R নাম দিয়া হ’ল।
পর্যায় 3: A বিন্দু কেন্দ্র কৰি আগৰ সমান ব্যাসার্দ্ধ লৈ AB ক কটাকৈ এটা বৃত্তচাপ আঁকা হ’ল। এই বৃত্তচাপে AB ক X বিন্দু কাটিছে।
পর্যায় 4: X বিন্দুক কেন্দ্ৰ কৰি RS ৰ সমান ব্যাসার্দ্ধ লৈ এটা বৃত্তচাপ আঁকা হ’ল। এই বৃত্তচাপে আগৰ বৃত্তচাপটোক Y বিন্দুত কাটিছে।
পর্যায় 5: AY সংযোগ কৰি l সৰলৰেখা অঁকা হ’ল। এই l সৰলৰেখাই হ’ল A বিন্দুৰ মাজেৰে যোৱা সমান্তৰাল ৰেখা।
2. 10 চে.মি. জোখৰ এডাল ৰেখাখণ্ড AB আঁকা। ৰেখাখণ্ডডালৰ A বিন্দুত এডাল ৰশ্মি AX আঁকা যাতে ∠BAX = 60° হয়। AX ৰ ওপৰত D এটা বিন্দু লোৱা যাতে AD = 4 চে.মি.। এতিয়া D বিন্দুৰ মাজেৰে AB ৰ সমান্তৰাল হোৱাকৈ এডাল ৰেখা আঁকা।
উত্তৰঃ অংকন প্রণালীঃ 10 চে.মি. এডাল ৰেখাখণ্ড AB অঁকা হ’ল। A বিন্দুত ∠BAX = 60° অঁকা হ’ল।
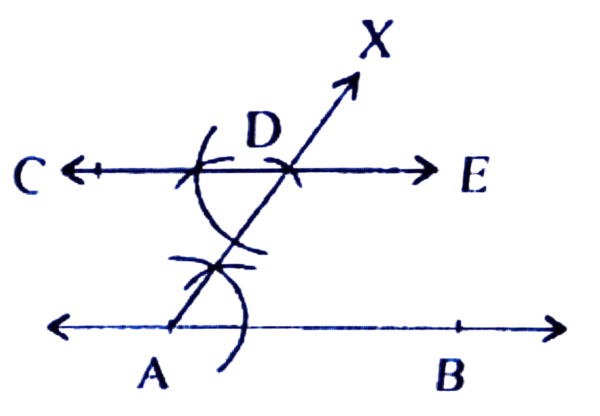
AX ৰ পৰা AD = 4 চে.মি. কাটি লোৱা হ’ল। D বিন্দুত ∠BAX = 60° ৰ অংকন কৰা হ’ল যাতে ∠CDA = 60° হয়। CD ক E বিন্দুলৈ বৰ্দ্ধিত কৰা হ’ল। এই CE য়েই AB ৰ সমান্তৰাল ৰেখা।
3. এডাল যিকোনো ৰেখা PQ আঁকা। PQ ৰ যিকোনো বিন্দুত এডাল লম্ব আঁকা। লম্বডালৰ ওপৰত PQ ৰ পৰা 5.6 চে.মি. দূৰত্বত এটা বিন্দু R লোৱা। R বিন্দুৰ মাজেৰে যোৱাকৈ PQ ৰ সমান্তৰাল এডাল ৰেখা আঁকা।
উত্তৰঃ
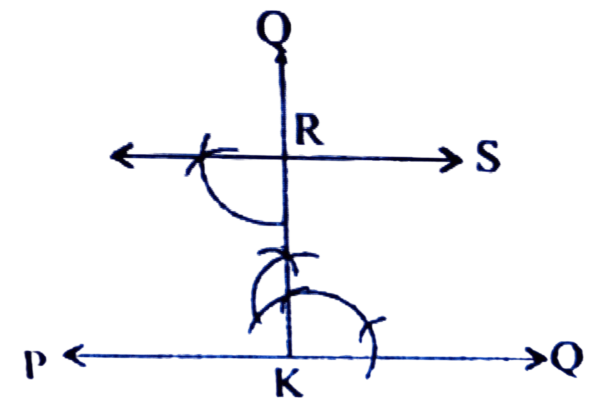
যিকোনো এডাল ৰেখা PQ লোৱা হ’ল। PQ ৰ K বিন্দুত KR লম্ব আঁকা হ’ল যাতে KR = 5.6 চে.মি. হয়। R বিন্দুৰ মাজেৰে KR ৰ ওপৰত এডাল লম্ব টনা হ’ল। এতিয়া এই লম্বডালে PQ ৰ সমান্তৰাল হ’ব।
4. 7.5 চে.মি. দৈর্ঘ্যৰ এডাল ৰেখাখণ্ড XY আঁকা। X আৰু Y বিন্দুত দুডাল লম্ব অংকন কৰা। লম্ব দুডালৰ ওপৰত ৰেখাডালৰ পৰা 5 চে.মি. দূৰত্বত দুটা বিন্দু ক্রমে A আৰু B লোৱাঁ। A বিন্দুৰ মাজেৰে XY ৰ সমান্তৰাল এডাল ৰেখা আঁকা। ৰেখাডাল B বিন্দুৰ মাজেৰে পাৰ হৈ যাবনে?
উত্তৰঃ
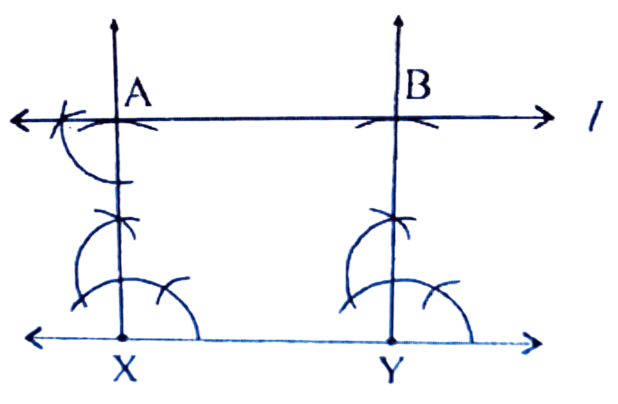
7.5 চে.মি. দৈর্ঘ্যৰ এডাল XY ৰেখাখও আঁকা হ’ল। X আৰু Y বিন্দুত দুডাল লম্ব অংকন কৰা হ’ল যাতে লম্বদুডালৰ ওপৰত ৰেখাডালৰ পৰা 5 চে.মি. দূৰম্বত দুটা বিন্দু A আৰু B থাকে। A বিন্দুৰ মাজেৰে XY ৰ সমান্তৰালকৈ I ৰেখাডাল অংকন কৰা হ’ল। এই ৰেখাডাল B বিন্দু মাজেৰেও যাব।
অনুশীলনী – 10.2 |
|---|
1. ABC অংকন কৰা যাতে–
(i) AB = 3 চে.মি.
BC = 4 চে.মি.
AC = 2.5 চে.মি.
উত্তৰঃ
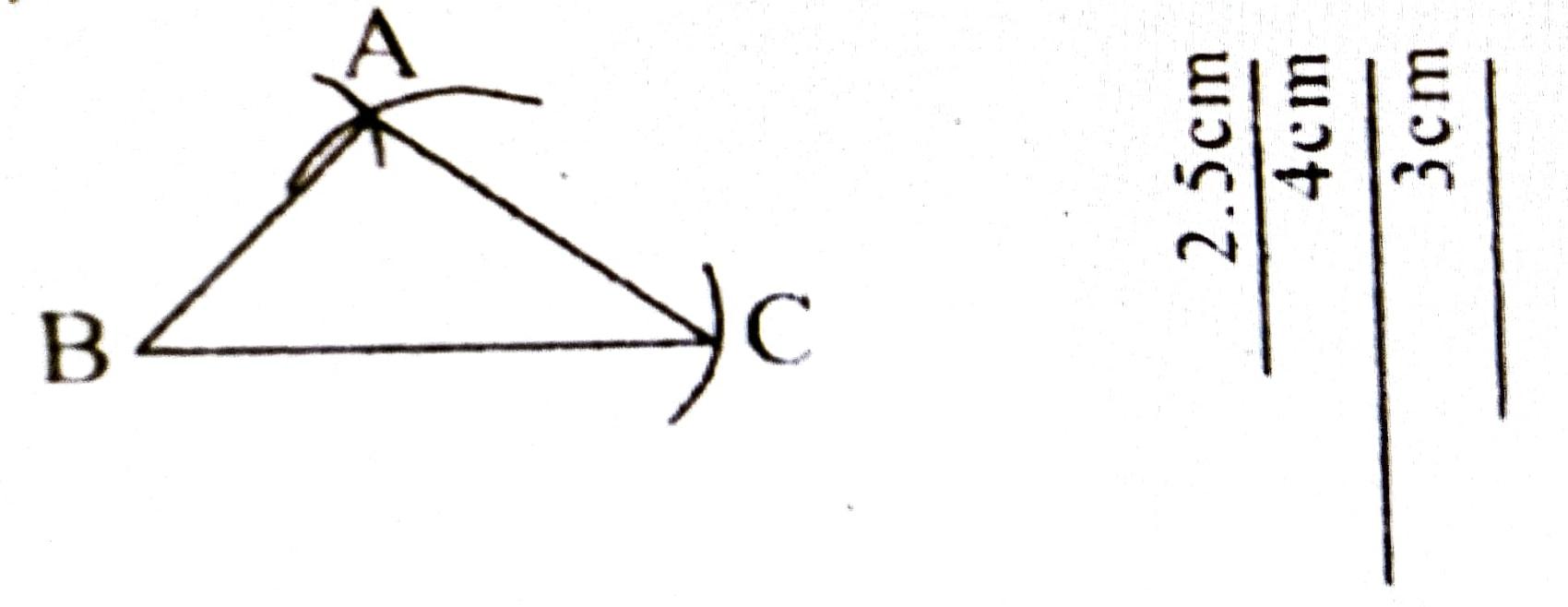
অংকন প্রণালীঃ দিয়া আছে, AB = 3 চে.মি., BC = 4 চে.মি., AC = 2.5 চে.মি., BC = 4 চে.মি. লোৱা হ’ল। B বিন্দুক কেন্দ্ৰ কৰি 3 চে.মি. ব্যাসাৰ্দ্ধৰ এটা বৃত্তচাপ অঁকা হ’ল। আকৌ C বিন্দু কেন্দ্র কৰি 2.5 চে.মি. ব্যাসার্দ্ধৰ বৃত্তচাপ অঁকা হ’ল। দুয়োটা চাপে কটাকটি কৰা এই বিন্দুটোৰ নাম A দিয়া হ’ল। A, B আৰু A, C সংযোগ কৰা হ’ল। এই ABC য়েই আঁকিবলগীয়া ত্রিভুজ।
(ii) AB = 6 চে.মি.
BC = 4 চে.মি.
AC = 7 চে.মি.
উত্তৰঃ
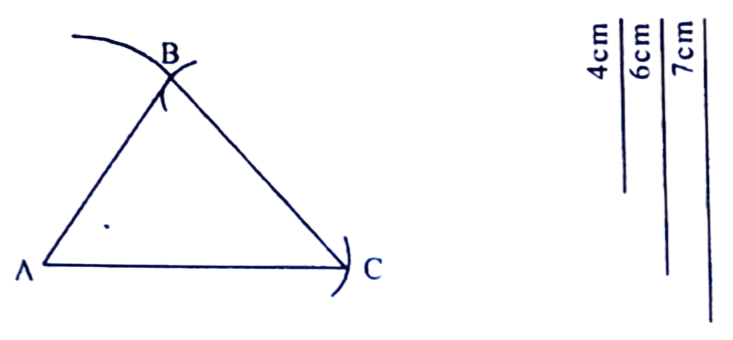
অংকন প্রণালীঃ দিয়া আছে, AB = 6 চে.মি., BC = 4 চে.মি., AC = 7 চে.মি., BC = 6 চে.মি. লোৱা হ’ল। B বিন্দুক কেন্দ্ৰ কৰি 4 চে.মি. ব্যাসার্দ্ধৰ এটা বৃত্তচাপ অঁকা হ’ল। আকৌ C বিন্দু কেন্দ্র কৰি 7 চে.মি. ব্যাসাৰ্দ্ধৰ বৃত্তচাপ অঁকা হ’ল। দুয়োটা চাপে কটাকটি কৰা এই বিন্দুটোৰ নাম A দিয়া হ’ল। A, B আৰু A, C সংযোগ কৰা হ’ল। এই ABC য়েই আঁকিবলগীয়া ত্রিভুজ।
2. এটা সমদ্বিবাহু ত্রিভুজ অংকন কৰা যাৰ ভূমিৰ দীঘ 5 চে.মি. আৰি সমান বাহু দুটাৰ প্ৰতিটোৰ দীঘ 4 চে.মি.।
উত্তৰঃ
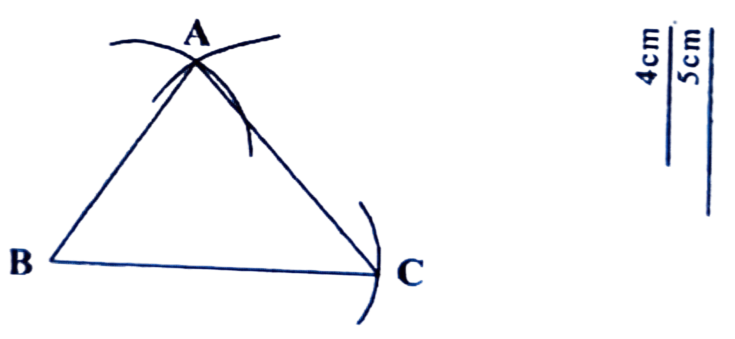
অংকন প্ৰণালীঃ ধৰাহ’ল BC ভূমি 5 চে.মি.। BC ৰ B বিন্দুৰ পৰা এটা 4 চে.মি. ৰ দৈৰ্ঘ্যৰ বৃত্তচাপ অঁকা হ’ল। আকৌ C বিন্দুৰ পৰা ও 4 চে.মি. দৈর্ঘ্যৰ বৃত্তচাপ অংকন কৰা হ’ল যাতে দুয়োটা চাপে A বিন্দুত কটাকটি কৰে। A, B আৰু A, C সংযোগ কৰা হ’ল। এই ABC য়েই আঁকিবলগীয়া সমদ্বিবাহু ত্রিভুজ।
3. এটা সমবাহু ত্রিভুজ DEF ৰ DE = 6.5 চে.মি। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
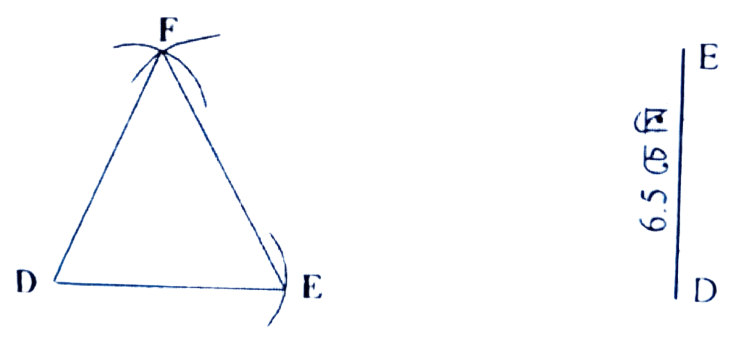
অংকন প্ৰণালীঃ ধৰাহ’ল DE ভূমি 6.5 চে.মি.। DE ৰ D বিন্দুৰ পৰা ওপৰৰ ফালে এটা 6.5 চে.মি. দৈৰ্ঘ্যৰ বৃত্তচাপ অঁকা হ’ল। আকৌ E বিন্দুৰ পৰাও 6.5 চে.মি. দৈর্ঘ্যৰ বৃত্তচাপ অংকন কৰা হ’ল যাতে দুয়োটা চাপ F বিন্দুত কটাকটি কৰে। F, D আৰু F, E সংযোগ কৰা হ’ল। এই DEF য়েই আঁকিবলগীয়া সমবাহু ত্রিভুজ।
4. ∆ΧΥΖ ৰ XY = YZ = 5.5 চে.মি. আৰু XZ = 4 চে.মি.। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
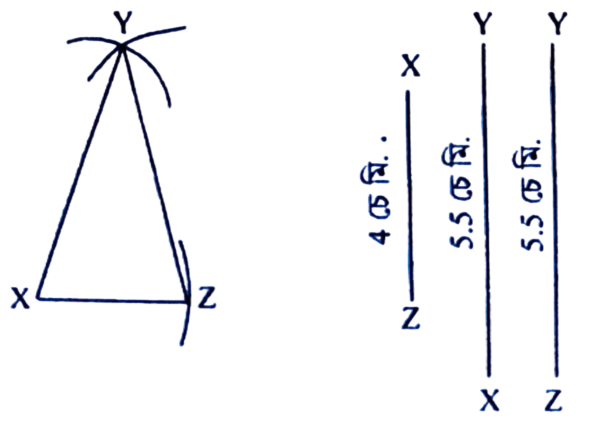
অংকন প্রণালীঃ ধৰাহ’ল XZ ভূমি 4 চে.মি. লোৱা হ’ল। XZ ৰ Z বিন্দুৰ পৰা ওপৰৰ ফালে এটা 5.5 চে.মি. ৰ দৈৰ্ঘ্যৰ এটা বৃত্তচাপ অঁকা হ’ল। আকৌ Z বিন্দুৰ পৰাও 5.5 চে.মি. দৈৰ্ঘ্যৰ বৃত্তচাপ অংকন কৰা হ’ল যাতে দুয়োটা চাপে Y বিন্দুত কটাকটি কৰে। Y, X আৰু Y, Z সংযোগ কৰা হ’ল। এই XYZ য়েই আঁকিবলগীয়া ত্রিভুজ।
অনুশীলনী – 10.3 |
|---|
1. ∆АВС ৰ AB = 6 চে.মি., BC = 7 চে.মি. আৰু ∠B = 75°। ত্রিভুজ অংকন কৰা।
উত্তৰঃ
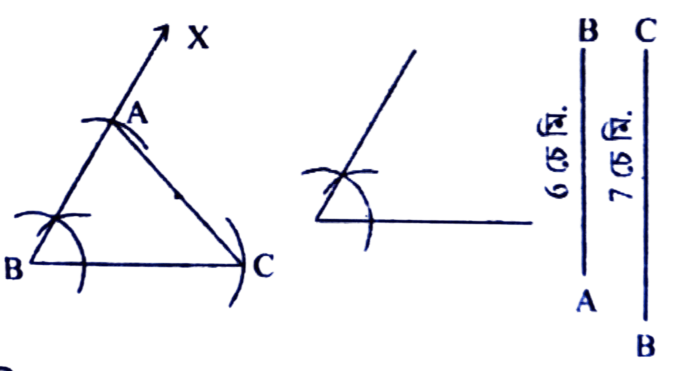
অংকন প্রণালীঃ BC = 7 চে.মি. লোৱা হ’ল। B বিন্দুত ∠CBX = 75° মাপৰ কোণ এটা অংকন কৰা হ’ল। BX ৰ পৰা AB = 6 চে.মি. লোৱা হ’ল। C ৰ পৰা A বিন্দুলৈ এডাল ৰেখাখণ্ড টনা হ’ল। এইটোৱেই আঁকিবলগীয়া ABC ত্রিভুজ।
2. ∆PQR ৰ QR = PR = 8 চে.মি. আৰু ∠R = 60° হ’লে ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
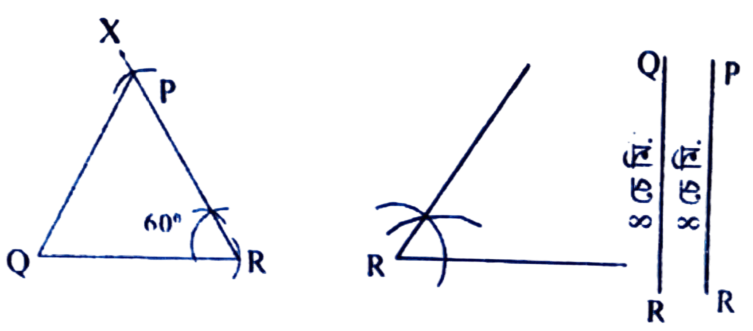
অংকন প্রণালীঃ QR = 8 চে.মি. লোৱা হ’ল। R বিন্দুত ∠QRP = 60° মাপৰ কোণ এটা অংকন কৰা হ’ল। RX ৰ পৰা RP = 8 চে.মি. লোৱা হ’ল। Q ৰ পৰা P বিন্দুলৈ এডাল ৰেখাখণ্ড টনা হ’ল। এইটোৱেই আঁকিবলগীয়া PQR ত্রিভুজ।
3. ∆DEF ৰ DE = 5.5 চে.মি., DF = 7.5 চে.মি. আৰু ∠D = 80° ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
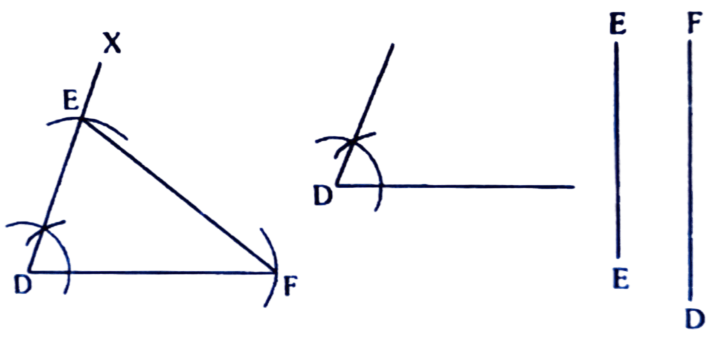
অংকন প্রণালীঃ DF = 7.5 চে.মি. লোৱা হ’ল। D বিন্দুত ∠FDX = 80° মাপৰ কোণ এটা অংকন কৰা হ’ল। DX ৰ পৰা DE = 5.5 চে.মি. লোৱা হ’ল। F ৰ পৰা E বিন্দুলৈ এডাল ৰেখাখণ্ড টনা হ’ল। এইটোৱেই আঁকিবলগীয়া DEF ত্রিভুজ।
4. এটা সমকোণী ত্রিভুজ অংকন কৰা যাৰ লম্ব বাহু দুটাৰ প্ৰতিটোৰে মাপ 4.5 চে.মি.।
উত্তৰঃ
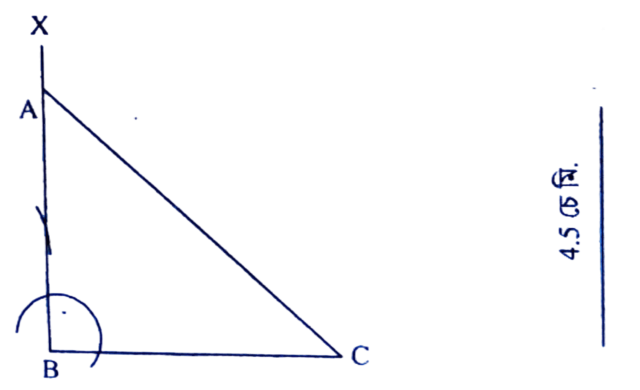
অংকন প্রণালীঃ BC = 4.5 চে.মি. লোৱা হ’ল। B বিন্দুত ∠CBX = 90° মাপৰ কোণ এটা অংকন কৰা হ’ল। BX ৰ পৰা BA = 4.5 চে.মি. লোৱা হ’ল। C ৰ পৰা A বিন্দুলৈ এডাল ৰেখাখণ্ড টনা হ’ল। এইটোৱেই আঁকিবলগীয়া ABC সমকোণী ত্রিভুজ।
5. এটা ত্রিভুজৰ দুটা বাহুৰ মাপ 5.5 চে.মি. আৰু 6.5 চে.মি. আৰু বাহু দুটাৰ মাজৰ কোণটোৰ মাপ 120°। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
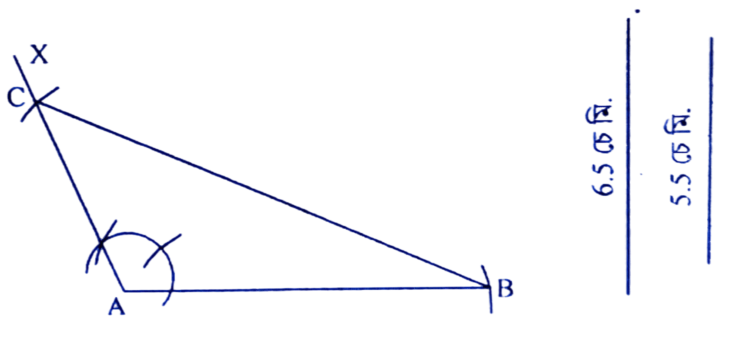
অংকন প্রণালীঃ AB = 6.5 চে.মি. লোৱা হ’ল। A বিন্দুত ∠BAX = 120° মাপৰ কোণ এটা অংকন কৰা হ’ল। AX ৰ পৰা AC = 5.5 চে.মি. লোৱা হ’ল। B ৰ পৰা C বিন্দুলৈ এডাল ৰেখাখণ্ড টনা হ’ল। এইটোৱেই আঁকিবলগীয়া ABC ত্রিভুজ।
অনুশীলনী – 10.4 |
|---|
1. ∆ΑΒC ৰ ∠B = 65°, ∠C = 55° আৰু BC = 7 চে.মি.। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
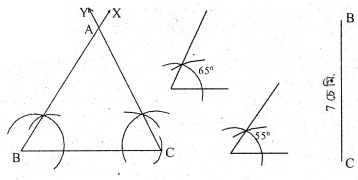
অংকন প্রণালীঃ C = 7 চে.মি. লোৱা হ’ল। B বিন্দুত ∠CBX = 65° আৰু ∠BCY = 55° মাপৰ কোণ দুটা অংকন কৰা হ’ল। BX আৰু CY ৰশ্মি দুডালে পৰস্পৰ A বিন্দুত কটাকটি কৰিছে। এই ABC য়েই আঁকিবলগীয়া ত্রিভুজ।
2. এটা ত্রিভুজৰ এটা বাহুৰ মাপ 6.5 চে.মি.। এই বাহুটোৰ দুই মূৰৰ কোণ দুটাৰ মাপ ক্রমে 45° আৰু 75°। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
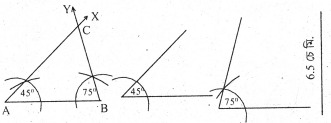
অংকন প্রণালীঃ AB = 6.5 চে.মি. লোৱা হ’ল। A বিন্দুত ∠BAX = 45° আৰু B বিন্দুত ∠ABY = 75° মাপৰ কোণ দুটা অংকন কৰা হ’ল। BX আৰু CY ৰশ্মি দুডালে পৰস্পৰ A বিন্দুত কটাকটি কৰিছে। এই ABC য়েই আঁকিবলগীয়া ত্রিভুজ।
3. ∆PQR ৰ ∠P = 60°, ∠Q = 50° আৰু QR = 6 চে.মি.। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
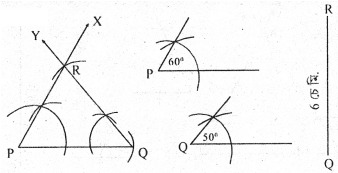
অংকন প্রণালীঃ PQ = 6 চে.মি. লোৱা হ’ল। P বিন্দুত ∠QPX = 60° আৰু Q বিন্দুত ∠PQY = 50° মাপৰ কোণ দুটা অংকন কৰা হ’ল। PX আৰু QY ৰশ্মি দুডালে পৰস্পৰ R বিন্দুত কটাকটি কৰিছে। এই PQE য়েই আঁকিবলগীয়া ত্রিভুজ।
4. ∆ΧΥΖ ৰ XZ = 5.5। ∠X = 100°, ∠Z = 30°। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
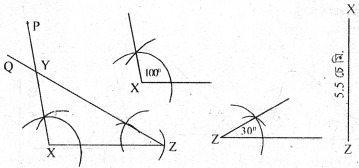
অংকন প্রণালীঃ XZ = 5.5 চে.মি. লোৱা হ’ল। X বিন্দুত ∠ZXP = 100° আৰু Z বিন্দুত ∠XZQ = 100° মাপৰ কোণ দুটা অংকন কৰা হ’ল। ZQ আৰু XP ৰশ্মি দুডালে পৰস্পৰ Y বিন্দুত কটাকটি কৰিছে। এই XYZ য়েই আঁকিবলগীয়া ত্রিভুজ।
অনুশীলনী – 10.5 |
|---|
1. ∆ABC ৰ ∠A সমকোণ। BC = 8 চে.মি., AB = 5 চে.মি.। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
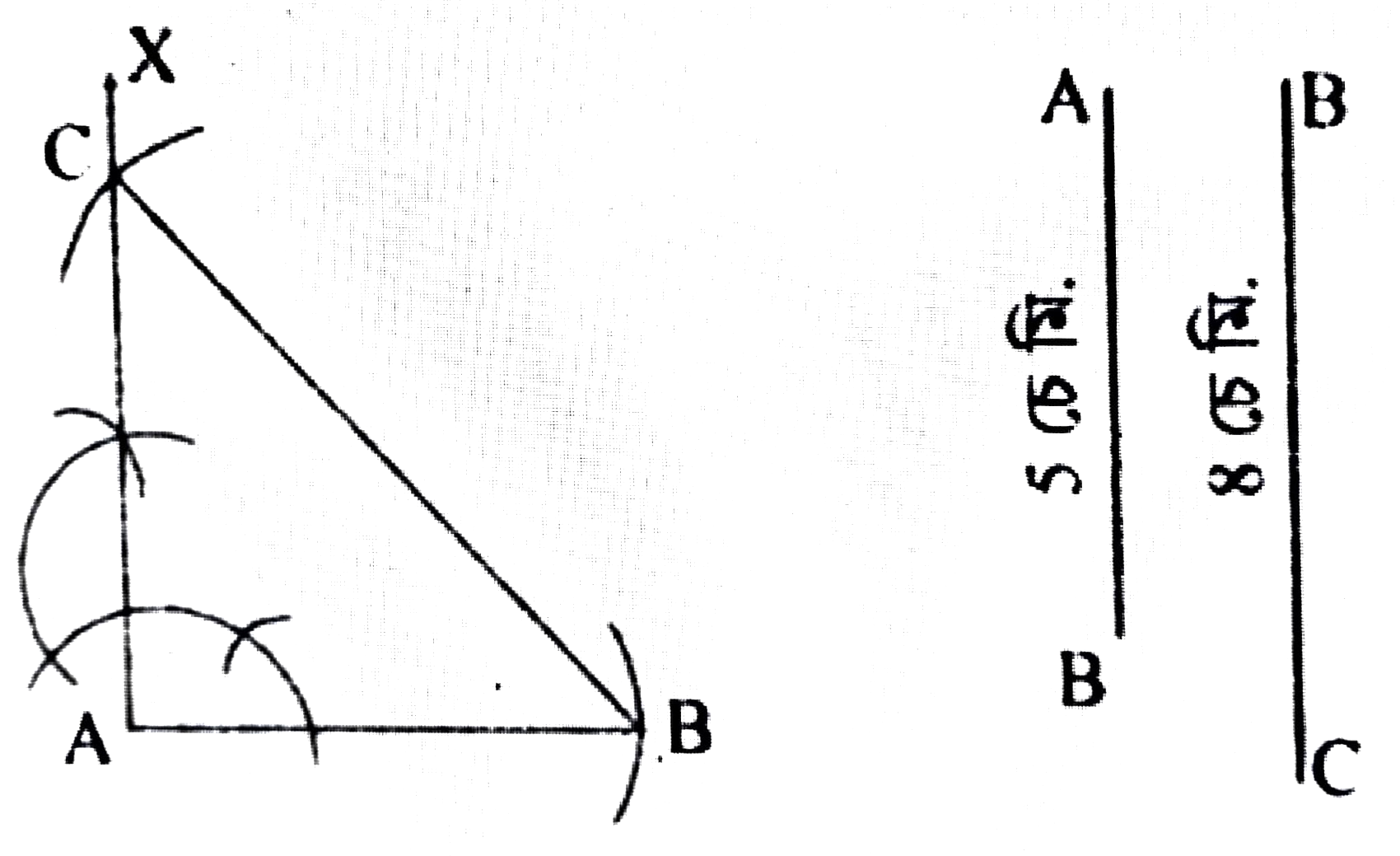
অংকন প্রণালীঃ 5 চে.মি. জোখৰ AB ৰেখাখণ্ড অঁকা হ’ল। A বিন্দুত 90° মাপৰ কোণ ∠BAX অঁকা হ’ল। B বিন্দুক কেন্দ্ৰ কৰি AX ক কটাকৈ C বিন্দুত কটাকৈ 8 চে.মি. দৈর্ঘ্যৰ এটা বৃত্তচাপ অঁকা হ’ল। B, C সংযোগ কৰা হ’ল। এই ABC য়েই আঁকিবলগীয়া সমকোণী ত্রিভুজ।
2. এটা সমকোণী ত্রিভুজৰ অতিভুজৰ মাপ 10 চে.মি. আৰু আন এটা বাহুৰ মাপ 6 চে.মি.। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
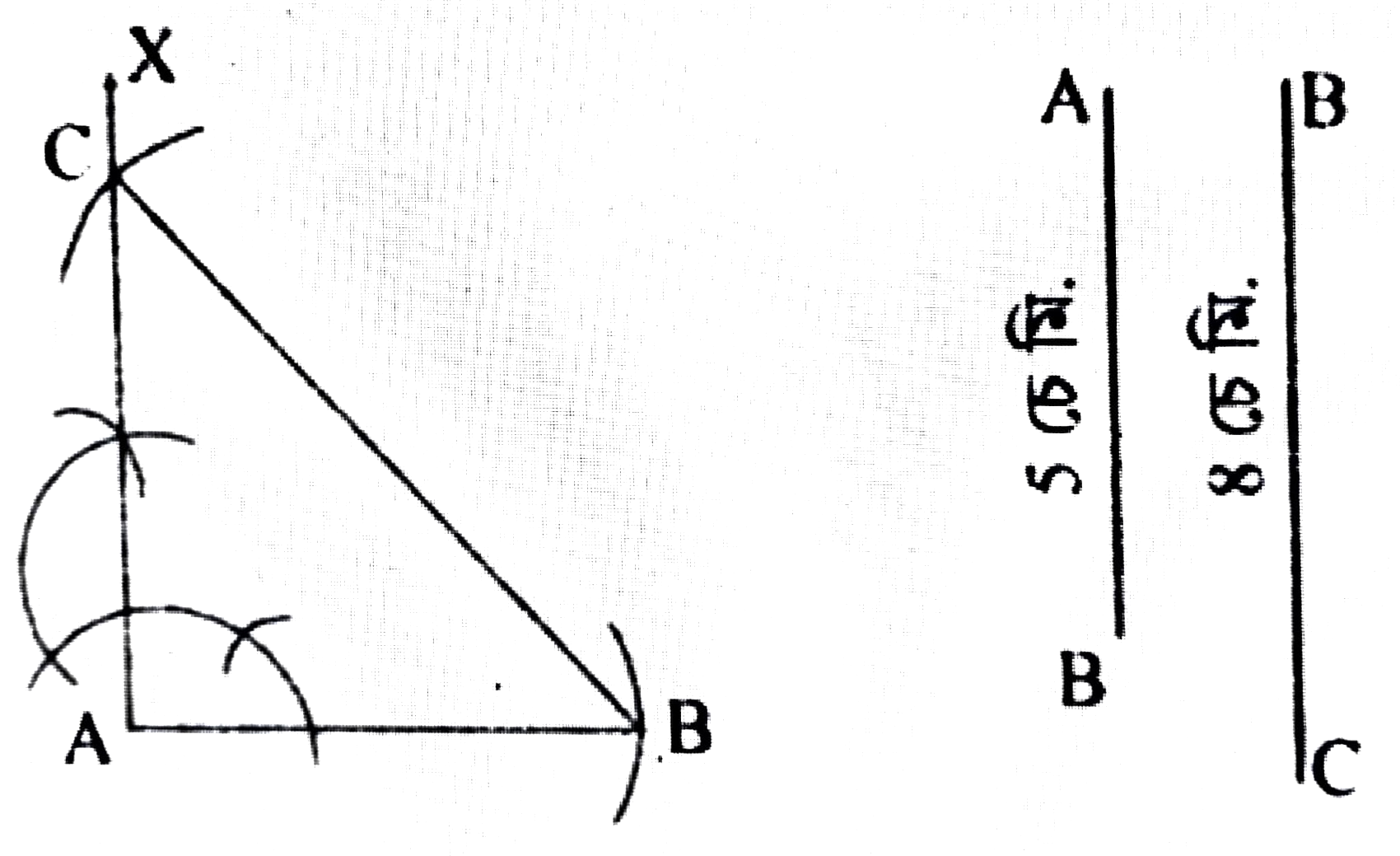
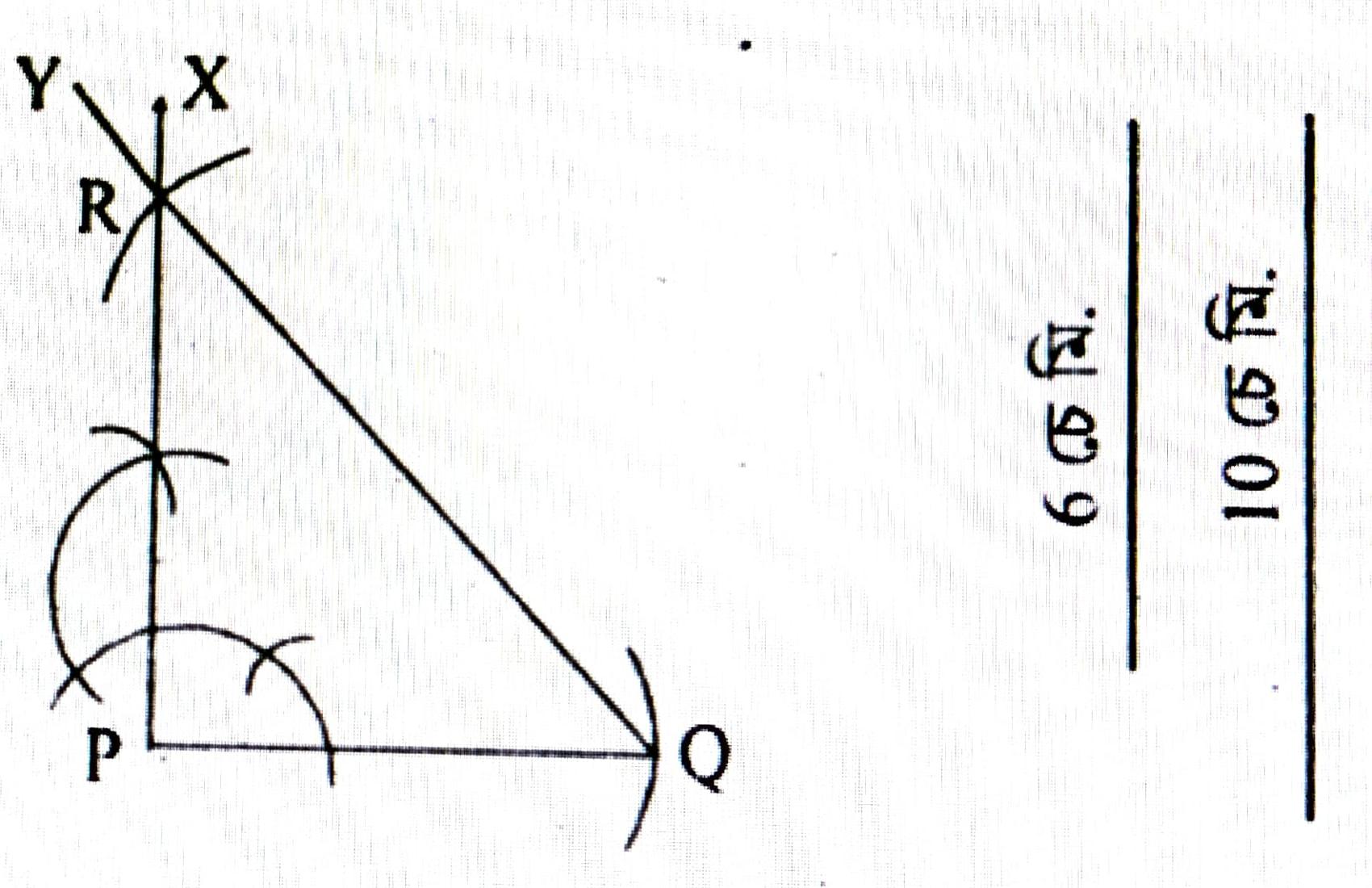
অংকন প্রণালীঃ 6 চে.মি. জোখৰ PQ ৰেখাখণ্ড অঁকা হ’ল । PQ ৰেখাৰ P বিন্দুত PX লম্ব অঁকা হ’ল। Q বিন্দুক, কেন্দ্ৰ কৰি PX ক R বিন্দুত কটাকৈ 10 চে.মি. দৈর্ঘ্যৰ এটা বৃত্তচাপ অঁকা হ’ল। R, Q সংযোগ কৰা হ’ল। এই PQR য়েই আঁকিবলগীয়া সমকোণী ত্রিভুজ।
3. ∆PQR ৰ ∠Q = 90°, PR = 7.5 চে.মি. আৰু PQ = 5 চে.মি.। ত্রিভুজটো অংকন কৰা।
উত্তৰঃ
অংকন প্রণালীঃ 5 চে.মি. জোখৰ PQ ৰেখাখও অঁকা হ’ল। Q বিন্দুত 90° মাপৰ কোণ ∠PQX অঁকা হ’ল। P বিন্দুক কেন্দ্ৰ কৰি PX ক কটাকৈ 7.5 চে.মি. দৈর্ঘ্যৰ এটা বৃত্তচাপ অঁকা হ’ল। চাপটোৱে R বিন্দুত কাটিছে। PQ সংযোগ কৰা হ’ল। এই PQR য়েই আঁকিবলগীয়া সমকোণী ত্রিভুজ।
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

