SEBA Class 7 Mathematics (Assamese Medium) Chapter 12 – বীজগণিতীয় ৰাশি Solutions & Summary
Find SEBA Class 7 Mathematics Chapter 12 – “বীজগণিতীয় ৰাশি” (Algebraic Expressions) solutions, designed for Assamese medium students. This chapter explains the concept of variables, constants, algebraic terms, and operations on algebraic expressions.
Students will learn about addition, subtraction, multiplication, and division of algebraic expressions, along with special identities and their applications. The chapter also covers factorization techniques and simplification methods for algebraic expressions.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students build a strong foundation in algebra and perform well in exams.
To access solutions for all chapters, Click Here
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীলনী – 12.1 |
|---|
1. তলৰ ক্ষেত্ৰবোৰত চলক, ধ্রুৱক আৰু পাটিগণিতৰ প্ৰক্ৰিয়া ব্যৱহাৰ কৰি বীজগণিতীয় ৰাশিসমূহ লিখা।
(i) x সংখ্যাটোক x ৰে পূৰণ কৰি 2 যোগ কৰা।
উত্তৰঃ x × x + 2
= x² + 2
(ii) a আৰু b ৰ যোগফল।
উত্তৰঃ a আৰু b ৰ যোগফল
= a + b
(iii) x ৰ পৰা 7 বিয়োগ।
উত্তৰঃ x ৰ পৰা 7 বিয়োগ
= x – 7
(iv) y ৰ পৰা z বিয়োগ।
উত্তৰঃ y ৰ পৰা z বিয়োগ
= y – z
(v) ‘x’ ৰ বৰ্গক y ৰে পূৰণ, পূৰণফলৰ লগত z ৰ যোগ।
উত্তৰঃ ‘x’ ৰ বৰ্গক y ৰে পূৰণ, পূৰণফলৰ লগত z ৰ যোগ
= (x² × y + z)
= x²y + z
(vi) x আৰু y ৰ পূৰণফলৰ আধা।
উত্তৰঃ x আৰু y ৰ পূৰণফলৰ আধা
= 1/2 (x × y) = xy/2
(vii) y আৰু z ৰ পূৰণফলৰ পৰা y আৰু z যোগফল বিয়োগ।
উত্তৰঃ y আৰু z ৰ পূৰণফলৰ পৰা y আৰু z যোগফল বিয়োগ
= (y × z) – (y + z) = yz – (y + z)
(viii) x ক y ৰে হৰণ কৰি হৰণফলৰ লগত z যোগ।
উত্তৰঃ x ক y ৰে হৰণ কৰি হৰণফলৰ লগত z যোগ
= x/y + z
(ix) x ৰ 3 গুণৰ সৈতে z যোগ।
উত্তৰঃ x ৰ 3 গুণৰ সৈতে z যোগ
= x × 3 + z = 3x + z
(x) x ৰ লগত 6 যোগ কৰি, যোগফলক 3 ৰে হৰণ।
উত্তৰঃ x ৰ লগত 6 যোগ কৰি, যোগফলক 3 ৰে হৰণ
= (x + 6)/3
(xi) x ক 5 ৰে পূৰণ কৰি, পূৰণফলৰ বৰ্গ।
উত্তৰঃ x ক 5 ৰে পূৰণ কৰি, পূৰণফলৰ বৰ্গ
= (x × 5)²
(xii) x ৰ বৰ্গৰ সৈতে 5 পূৰণ।
উত্তৰঃ x ৰ বৰ্গৰ সৈতে 5 পূৰণ
= x² × 5 = 5x²
2. তলত দিয়া 5 টা পাত্রত প্রতিটোত ‘n’ টাকৈ চকলেট আছে।

(i) যদি প্রতিটো পাত্ৰত আকৌ 2 টাকৈ চকলেট ভৰাই দিয়া হয় তেন্তে সর্বমুঠ কিমানটা চকলেট থাকিব?
উত্তৰঃ প্রতিটো পাত্ৰত আকৌ 2 টা চকলেট ভৰালে সৰিগমুঠ চকলেট থাকিব = (2 × n) × 5
= 10n টা।
(ii) যদি n = 10 হয় তেন্তে সর্বমুঠ চকলেট কিমানটা হ’ব?
উত্তৰঃ n = 10
∴ সর্বমুঠ চকলেট হ’ব = 10n
= 10 × 10 = 100 টা।
3. তলৰ চিত্ৰটোত কেইটামান বল শাৰী আৰু স্তম্ভত সজোৱা আছে। সৰ্বমুঠ বলৰ সংখ্যা বীজগণিতীয় ৰাশিত প্রকাশ কৰা।
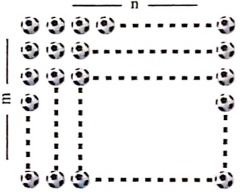
উত্তৰঃ শাৰীত থকা বলৰ সংখ্যা = n
স্তম্ভত থকা বলৰ সংখ্যা = m
∴ সৰ্বমুঠ বলৰ সংখ্যা = n × m = nm টা।
4. তলৰ ৰাশিবোৰৰ পদ আৰু সিহঁতৰ উৎপাদকসমূহ চিনাক্ত কৰা। বৃক্ষ চিত্ৰৰ সহায়ত পদ আৰু উৎপাদকসমূহ দেখুওৱাঃ
(a) y + 7
উত্তৰঃ y + 7 ৰাশিটোৰ পদ হ’ল y আৰু z
y = 1 × y পদটোৰ উৎপাদক 1, y
z = 1 × z পদটোৰ উৎপাদক 1, z
ৰাশি y + z
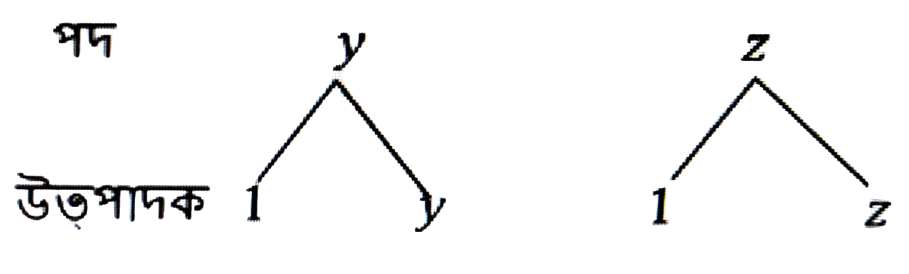
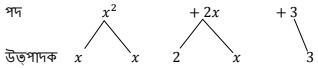
(b) x² + 2x + 3
উত্তৰঃ x² + 2x + 3 ৰাশিটোৰ পদ x², 2x, 3
x² = x × x পদটোৰ উৎপাদক x, x
2x = 2 × x পদটোৰ উৎপাদক 2, x
3 পদটোৰ উৎপাদক 3
ৰাশি x² + 2x + 3
(c) 2x² + 3xy + 4y²
উত্তৰঃ 2x² + 3xy + 4y² ৰাশিটোৰ পদ 2x², 3xy, 4y¹
2x² = 2 × x × x পদটোৰ উত্পাদক 3, x, y
3xy = 3 × x × y পদটোৰ উৎপাদক 2, x
4y² = 2 × 2 × y × y পদটোৰ উত্পাদক 2, 2, y, y
ৰাশি 2x² + 3xy + 4y²
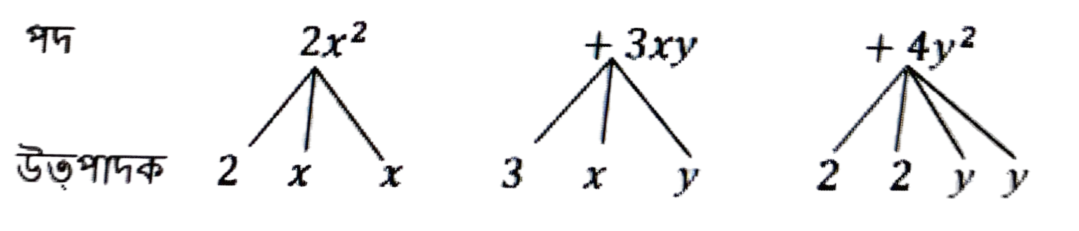
(d) 7x + 5
উত্তৰঃ 7x + 5 ৰাশিটোৰ পদ 7x, 5
7x ৰ উৎপাদক 7, x
5 ৰ উৎপাদক 5
ৰাশি 7x + 5
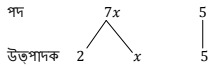
(e) xy – x + 1
উত্তৰঃ xy – x + 1 ৰাশিটোৰ পদ xy, -x, 1
xy = x × y ৰ ৰাশিটোৰ x, y
-x = -1 × x ৰ ৰাশিটোৰ পদ – 1, x
1ৰ ৰাশিটোৰ 1
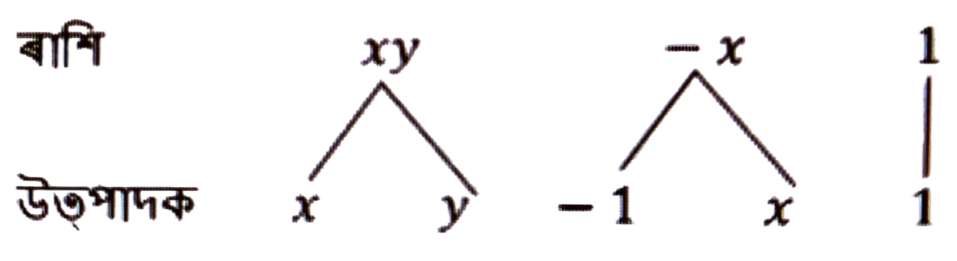
(f) 3x²y – 4xy²
উত্তৰঃ 3x²y – 4xy² ৰাশিটোৰ পদ 3x²y, -4xy²
3x²y – 3 × x × x × y ৰ উৎপাদক 3, x, x, y
-4xy² = -1 × 2 × 2 × x × y × yৰ উৎপাদক – 1, 2, 2, x, y, y
ৰাশি 3x²y – 4xy²

(g) 3x³ – x² + 1
উত্তৰঃ 3x³ – x² + 1 ৰাশিটোৰ পদ 3x³, -x², 1
3x³ = 3 × x × x × x ৰ উৎপাদক 3, x, x, x
-x² = -1 × x × x ৰ উৎপাদক -1, x, x
1ৰ উত্পাদক 1
ৰাশি 3x³ – x² + 1

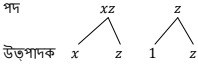
(h) xz + z
উত্তৰঃ xz + z ৰাশিটোৰ পদ xz, z
xz = x × z ৰ উৎপাদক x, z
z = 1 × z ৰ উৎপাদক x, z
ৰাশি xz + z
(i) -2mn + m² – 3n²
উত্তৰঃ -2mn + m³ – 3n² ৰাশিটোৰ পদ – 2mn, m³, -3n²
-2mn = -1 × 2 × m × n ৰ উৎপাদক – 1,2, m, n
m³ = m × m × m ৰ উৎপাদক m, m, m,
-3n² = -1 × 3 × n × nৰ উৎপাদক – 1, 3, n, n
ৰাশি -2mn + m³ – 3n²

(j) -7x² + 3x²y³ + 5x²y² – y
উত্তৰঃ -7x³ + 3x²y³ + 5x²y² – y ৰাশিটোৰ পদ 7x³, 3x²y³, 5x²y², -y
-7x³ = -1 × 7 × x × x ৰ উৎপাদক – 1,7, x, x, x
3x²y³ = 3 × x × x × y × y × y ৰ উৎপাদক 3, x, x, y, y, y
5x²y² = 5 × x × x × y × yৰ উৎপাদক 5, x, x, y, y
-y = -1 x y ৰ উতপাদক – 1, y
ৰাশি -7x³ + 3x²y³ + 5x²y² – y

5. তলত দিয়া তালিকাকেইখন সম্পূর্ণ কৰাঃ
(a)
|
ৰাশি |
পদ (যিটো ধ্ৰুৱক নহয়) |
সাংখ্যিক সহজ |
|
|---|---|---|---|
|
(i) |
2x + 3y |
||
|
(ii) |
mn + 3 |
||
|
(iii) |
2ab – a + b |
||
|
(iv) |
2x²y – 4xy² + 7 |
||
|
(v) |
3x³ – 7x² + y |
উত্তৰঃ
|
ৰাশি |
পদ (যিটো ধ্ৰুৱক নহয়) |
সাংখ্যিক সহজ |
|
|---|---|---|---|
|
(i) |
2x + 3y |
2x, 3y |
2, 3 |
|
(ii) |
mn + 3 |
mn |
1 |
|
(iii) |
2ab – a + b |
2a, -a, b |
2, -1, 1 |
|
(iv) |
2x²y – 4xy² + 7 |
2x²y, 4xy² |
2, -4 |
|
(v) |
3x³ – 7x² + y |
3x², 7x², y |
3, -7,1 |
(b)
|
ৰাশি |
x উৎপাদকযুক্ত পদ |
xৰ সহজ |
|
|---|---|---|---|
|
(i) |
xy³ + 1 |
||
|
(ii) |
2xy + y + 1 |
||
|
(iii) |
3xy² – xy + x |
||
|
(iv) |
7xz – z |
||
|
(v) |
y – x + 2 |
উত্তৰঃ
|
ৰাশি |
x উৎপাদকযুক্ত পদ |
xৰ সহজ |
|
|---|---|---|---|
|
(i) |
xy³ + 1 |
xy³ |
y³ |
|
(ii) |
2xy + y + 1 |
2xy |
2y |
|
(iii) |
3xy² – xy + x |
3xy², -xy, x |
3y², -y, 1 |
|
(iv) |
7xz – z |
7xz |
7z |
|
(v) |
y – x + 2 |
-x |
-1 |
(c)
|
ৰাশি |
b² উৎপাদকযুক্ত পদ |
b²ৰ সহজ |
|
|---|---|---|---|
|
(i) |
ab² + 9 |
||
|
(ii) |
ab² + a²b + 3a |
||
|
(iii) |
-b³ +3a²b -5b² |
উত্তৰঃ
|
ৰাশি |
b² উৎপাদকযুক্ত পদ |
b²ৰ সহজ |
|
|---|---|---|---|
|
(i) |
ab² + 9 |
ab² |
a |
|
(ii) |
ab² + a²b + 3a |
ab² |
a |
|
(iii) |
-b³ +3a²b -5b² |
-5b² |
5 |
6. তলত দিয়া ৰাশিবোৰ একপদ, দ্বিপদ, ত্রিপদ ৰাশি হিচাপে শ্রেণীভুক্ত কৰাঃ
(i) 2x + 3
উত্তৰঃ দ্বিপদ।
(ii) y³
উত্তৰঃ একপদ।
(iii) 3a²b
উত্তৰঃ একপদ।
(iv) 3a²b + 5ab² + 3a
উত্তৰঃ ত্রিপদ।
(v) 2m + 3n
উত্তৰঃ দ্বিপদ।
(vi) x² + x
উত্তৰঃ দ্বিপদ।
(vii) m² + n²
উত্তৰঃ দ্বিপদ।
(viii) 2x² + 3x + 1
উত্তৰঃ ত্রিপদ।
(ix) xy + y
উত্তৰঃ দ্বিপদ।
(x) 34
উত্তৰঃ একপদ।
7. (a) তলত দিয়া যোৰবোৰ সদৃশ নে বিসদৃশ লিখাঃ
(i) -4x, 1/2x
উত্তৰঃ সদৃশ।
(ii) -5x; 7y
উত্তৰঃ বিসদৃশ।
(iii) 9, 20
উত্তৰঃ সদৃশ।
(iv) 2x²y, 3xy²
উত্তৰঃ বিসদৃশ।
(v) 2xy, 3xz
উত্তৰঃ বিসদৃশ।
(vi) -7xz, 2xz
উত্তৰঃ সদৃশ।
(vii) x², x³
উত্তৰঃ বিসদৃশ।
(viii) x², 2x²
উত্তৰঃ সদৃশ।
(ix) mn, 3nm
উত্তৰঃ সদৃশ।
(x) 1/2z, 3/4z
উত্তৰঃ সদৃশ।
(b) তলৰ পদসমূহৰ পৰা সদৃশ পদবোৰ বাছি উলিওৱাঃ
ab², a², xy², y³, 4xy², 7ab², -2x, 5y, xy, 3x, -ab², a²b², 3ab², x³y³, 40x -m²n, 3mn², -m²n, 2a²b², 3y.
উত্তৰঃ প্রদত্ত পদসমূহৰ সদৃশ পদবোৰ-
ab², -ab², 7ab², 3ab²
xy², 4xy²
-2x, 3x, 40x
-m²n, -m²n
a²b², 2a²b²
5y, 3y
অনুশীলনী – 12.2 |
|---|
1. সদৃশ পদসমূহ একেলগ কৰি সৰল কৰাঃ
(i) 2x + 3y – 45 + 6y – 7x + 5
উত্তৰঃ 2x + 3y – 45 + 6y – 7x + 5
= (2x – 7x) + (3y + 6y) – (45 + 5)
= (2 – 7)x + (3 + 6)y(- 40)
= -5x + 9y – 40
(ii) x² – 2x + y² + 2x² + 4x + y³
উত্তৰঃ x² – 2x + y² + 2x² + 4x + y³
= (x² + 2x²) + (-2x + 4x) + y² + y³
= (1 + 2)x² + (-2 + 4)x + y² + y³
= 3x² + 2x + y² + y³
(iii) a – (2a – 3b) – b – (3b – 4a)
উত্তৰঃ a – (2a – 3b) – b – (3b – 4a)
= a – 2a + 3b – b – 3b + 4a
= (a – 2a + 4a) + (3b – b – 3b)
= (1 – 2 + 4)a + (3 – 1 – 3)b
= 3a + (-1)b
= 3a – b
(iv) x²y + 3xy² + y³ – 3x²y + 2xy² – 3y³ + 5
উত্তৰঃ x²y + 3xy² + y³ – 3x²y + 2xy² – 3y³ + 5
= (x²y + 3xy²) + (3xy² + 2xy²) + (y³ – 3x²) + 5
= (1 – 3)x²y + (3 + 2)xy² + (1 – 3)y³ + 5
= -2x²y + 5xy² – 2y³ + 5
(v) (2z² + 3y + 7) – (3y – 8z² + 1)
উত্তৰঃ (2z² + 3y + 7) – (3y – 8z² + 1)
= 2z² + 3y + 7 – 3y – 8z² + 1
= (2 + 8)z² + (3 – 3)y + 8
= 10z² + 0 × y + 8
= 10z² + 8
2. যোগ কৰাঃ
(i) 3x²y, -2x²y, 7x²y, 2x²y
উত্তৰঃ 3x²y, -2x²y, 7x²y, 2x²y
নির্ণেয় যোগফল = 3x²y + (-2x²y) + 7x²y + 2x²y
= 3x² – 2x²y + 7x²y + 2x²y
= (3 – 2 + 7 + 2)x²y
= 10x²y
(ii) x + xy, 3xy + x, x – 1
উত্তৰঃ x + xy, 3xy + x, x – 1
নির্ণেয় যোগফল = (x + xy) + (3xy + x)(x – 1)
= x + xy + 3xy + x + x – 1
= (x + x + x) + (xy + 3xy) – 1
= 3x + 4xy – 1
(iii) 2x² + 3xy + y², – 3x² + 5xy + 2y², x² – 8xy – 3y²
উত্তৰঃ 2x² + 3xy + y², – 3x² + 5xy + 2y², x² – 8xy – 3y²
নির্ণেয় যোগফল = (2x² + 3xy + y²) + (-3x² + 5xy + 2y²)(x² – 8xy – 3y²)
= 2x² + 3xy + y² – 3x² + 5xy + 2y² + x² – 8xy – 3y²
= (2x² – 3x² + x²) + (3xy + 5xy – 8xy) + (y² + 2y² – 3y²)
= (2 – 3 + 1)x² + (3 + 5 – 8)xy + (1 + 2 – 3)y²
= 0 × x² + 0 × xy + 0 × y²
= 0
(iv) 3x + 4y, – 7x + 5y + 2, 2x + 5xy + 7
উত্তৰঃ 3x + 4y, – 7x + 5y + 2, 2x + 5xy + 7
নির্ণেয় যোগফল = (3x + 4y) + (-7x + 5y + 2) + (2x + 5xy + 7)
= 3x + 4y – 7x + 5y + 2 + 12x + 5xy + 7
= (3x – 7x + 12x) + (4y + 5y) + 5xy + (2 + 7)
= (3 – 7 + 12)x + (4 + 5)y + 5xy + 9
= 8x + 9y + 5xy + 9
(v) 6xy, 7yx, 3xz, 5yz
উত্তৰঃ 6xy, 7yx, 3xz, 5yz
নির্ণেয় যোগফল = 6xy + 7yx + 3xz + 5yz
= 6xy + (7yz + 5yz) + 3xz
= 6xy + (7 + 5)yz + 3xz
= 6xy + 12yz + 3xz
(vi) 2x² – y² + 5, y² + 3 – x², x² + y² + 1
উত্তৰঃ 2x² – y² + 5, y² + 3 – x², x² + y² + 1
নির্ণেয় যোগফল = (2x² – y² + 5) + (y² + 3 – x²) + (x² + y² + 1)
= (2x² – y² + 5 + y² + 3 – x² + x² + y² + 1)
= (2x² – x² + x²) + (-y² + y² + y²) + (5 + 3 + 1)
= (2 – 1 + 1)x² + (-1 + 1 + 1)y² + 9
= 2x² + y² + 9
(vii) x²y² + xy + 1, -2x²y² + 3xy – 2, 3x²y² – 5xy + x
উত্তৰঃ x²y² + xy + 1, -2x²y² + 3xy – 2, 3x²y² – 5xy + x
নির্ণেয় যোগফল = (x²y² + xy + 1) + (-2x²y² + 3xy – 2) + (3x²y² – 5xy + x)
= x²y² + xy + 1 – 2x²y² + 3xy – 2 + 3x²y² – 5xy + x
= (x²y² – 2x²y² + 3x²y²) + (xy + 1 + 3xy – 5xy) + x + (1 – 2)
= 2x²y² + (-1)xy + x – 1
= 2x²y² + z², z² +1
(viii) 3y² + yz, – y² + 2yz + z², z² + 1
উত্তৰঃ 3y² + yz, – y² + 2yz + z², z² + 1
নির্ণেয় যোগফল = (3y² + yz) + (-y² + 2yz + z²) + (z² + 1)
= 3y² + yz – y² + 2yz + z² + z² + 1
= (3y² – y²) + (yz + 2yz) + (z² + z²) + 1
= (3 – 1)y² + (1 + 2)yz + (1 + 1)z² + 1
= 2y² + 3yz + 2z² + 1
3. বিয়োগ কৰাঃ
(i) 5x²y ৰ পৰা -7x²y
উত্তৰঃ 5x²y ৰ পৰা -7x²y
= 5x²y + 7x²y
= (5 + 7)x²y
= 12x²y
(ii) 7xy ৰ পৰা 2xy
উত্তৰঃ 7xy ৰ পৰা 2xy
= 7xy – 2xy
= (7 – 2)xy
= 5xy
(iii) 2x² + 3xy + 4y² ৰ পৰা -x² – 2xy + y²
উত্তৰঃ 2x² + 3xy + 4y² ৰ পৰা -x² – 2xy + y²
= (2x² + 3xy + 4y²) – (-x² – 2xy + y²)
= 2x² + 3xy + 4y² + x² – 2xy + y²
= (2x² + x²) + (3xy + 2xy) + (4y² – y²)
= (2 + 1)x² + (3 + 2)xy + (4 – 1)y²
= 3x² + 5xy + 3y²
(iv) 5x²y² + xy + 7 ৰ পৰা -2x²y² + 2xy + 5
উত্তৰঃ 5x²y² + xy + 7 ৰ পৰা -2x²y² + 2xy + 5
= (5x²y² + xy + 7) – (-2x²y² – 2xy + 5)
= 5x²y² + xy + 7 + 2x²y² – 2xy + 5
= (5x²y² + 2x²y²) + (xy – 2xy) + (7 – 5)
= (5 + 2)x²y² + (1 – 2)xy + 2
= 7x²y² + (-1)xy + 2
= 7x²y² – xy + 2
(v) 2m + 3n ৰ পৰা 2m² – 3m + 1
উত্তৰঃ 2m + 3n ৰ পৰা 2m² – 3m + 1
= (2m + 3n) – (2m² – 3m + 1)
= 2m + 3n – 2m² + 3m – 1
= (2m + 3m) + 3n – 2m² – 1
= (2 + 3)m + 3n – 2m² – 1
= 5m + 3n – 2m² – 1
(vi) 6pq – p² – q² ৰ পৰা 2pq + p² + q²
উত্তৰঃ 6pq – p² – q² ৰ পৰা 2pq + p² + q²
= (6pq – p² – q²) – (2pq + p² + q²)
= 6pq – p² – q² – 2pq + p² + q²
= (6pq – 2pq) + (-p² – q²) + (-p² – q²)
= (6 – 2)pq + (-1 – 1)p² + (-1 – 1)q²
= 4pq + (-2)p² + (-2)q²
= 4pq – 2p² – 2q²
(vii) 2p – 7 ৰ পৰা p² + 1
উত্তৰঃ 2p – 7 ৰ পৰা p² + 1
= (2p – 7) – (p² + 1)
= (2p – 7) – (p² + 1)
= 2p – 7 – p² – 1
= 2p – p² – (7 + 1)
= 2p – p² – 8
(viii) 3x² – 2x + 1 ৰ পৰা 4x² + 5x + 3
উত্তৰঃ 3x² – 2x + 1 ৰ পৰা 4x² + 5x + 3
= (3x² – 2x + 1) – (-4x² + 5x + 3)
= 3x² – 2x + 1 + 4x² + 5x + 3
= (3 + 4)x² + (-2 – 5)x + (-2)
= (3x² + 4x²) + (-2x – 5x) + (1 – 3)
= 7x² + (-7)x + (-2)
= 7x² – 7x – 2
4. দুটা বীজগণিতীয় ৰাশিৰ যোগফল 5x² + 2x + 1, এটা বাশি x² + 5x + 7 হ’লে আনটো ৰাশি উলিওৱা।
উত্তৰঃ বীজগণিতীয় ৰাশিৰ যোগফল = 5x² + 2x + 1
এটা ৰাশি = x² + 5x + 7
∴ আনটো ৰাশি = (5x² + 2x + 1) – (x² + 5x + 7)
= 5x² + 2x + 1 – x² + 5x + 7
= (5x² – x²) + (2x – 5x) + (1 – 7)
= (5 – 1)x² + (2 – 5)x + (-6)
= 4x² – 3x – 6
5. 7x + 3y + 1 পাবলৈ 2x + 4y + 7ৰ পৰা কিমান বিয়োগ কৰিব লাগিব?
উত্তৰঃ নির্ণেয় বিয়োগ কৰিবলগীয়া ৰাশি = (2x + 4y + 7) – (7x + 3y + 1)
= 2x + 4y + 7 – 7x – 3y – 1
= (2x – 7x) + (4y – 3y) + (7 – 1)
= (2 – 7)x + (4 – 3)y + 6
= 5x + y + 6
6. অনিমা, মামণি, ৰীতা আৰু পূৰৱীৰ গণিতৰ পৰীক্ষাৰ ফলাফল এনে ধৰণৰ–
অনিমাতকৈ মামণিয়ে দুগুণ নম্বৰ পাইছে
ৰীতাই অনিমাতকৈ 4 নম্বৰ কম পাইছে
পূৰৱীয়ে মামণিতকৈ 2 নম্বৰ বেছি পাইছে
এতিয়া চাৰিওজনীয়ে পোৱা নম্বৰৰ যোগফল বীজগণিতীয় ৰাশিত প্রকাশ কৰা।
উত্তৰঃ ধৰা হ’ল মামণিয়ে নম্বৰ পায় x
∴ অনিতাই নম্বৰ পায় 2x
ৰীতাই নম্বৰ পায় 2x – 4
পূৰৱীযে নম্বৰ পায় x + 2
∴ চাৰিওজনীয়ে পোৱা নম্বৰৰ যোগফল = x + 2x + (2x – 4) + (x + 2)
= x + 2x + 2x – 4 + x + 2
= 6x – 2
7. 3x² + 2x + 1 আৰু y² – 4x – 2ৰ যোগফলৰ পৰা 2x² + y² + 7x + 3 বিয়োগ কৰা।
উত্তৰঃ [(3x² + 2x + 1) + (y² – 4x – 2)] – (2x² + y² + 7x + 3)
= [3x² + 2x + 1 + y² – 4x – 2] – (2x² + y² + 7x + 3)
= [3x² + (2x – 4x) + y² + (1 – 2)] – (2x² + y² + 7x + 3)
= (3x² – 2x + y² – 1) – (2x² + y² + 7x + 3)
= 3x² – 2x + y² – 1 – 2x² – y² – 7x – 3
= (3x² – 2x²) + (2x – 7x) + (-1 – 3)
= (3 – 2)x² + (-2 – 7)x + (-4)
= x² + (-9)x – 4
= x² – 9x – 4
8. 2x² + 7x আৰু 3x – 7 ৰ সমষ্টিৰ পৰা 2x² – x আৰু x² + 6x + 2 ৰ সমষ্টি বিয়োগ কৰা।
উত্তৰঃ [(2x² + 7x) + (3x – 7)] – [(2x² – x) + (x² + 6x + 2)]
= [2x² + 7x + 3x – 7] – [2x² – x + x² + 6x + 2]
= (2x² + 10x – 7) – (3x² + 5x + 2)
= 2x² + 10x – 7 – 3x² – 5x – 2
= (2x² – 3x²) + (10x – 5x) – 7 – 2
= (2 – 2)x² + (10 – 5)x + (-9)
= -x² + 5x – 9
9. এডৰা খেতিৰ মাটিৰ চাৰিসীমাৰ জোখ ক্রমে x, x/2, y আৰু y/2 । মাটি টুকুৰাৰ পৰিসীমা কিমান?
উত্তৰঃ মাটিডৰাৰ চাৰিসীমাৰ জোখ ক্রমে x, x/2,y আৰু y/2
∴ মাটিডৰাৰ পৰিসীমা = x + x/2 + y + y/2
= (1 + 1/2)x + (1+ 1/2)y
= 3/2x + 3/2y
= 3/2(x + y)
10. নবীনৰ হাতত কেইটামান মার্বল আছে। বিজয়ৰ হাতত নবীনৰ হাতত থকা মাৰ্বলৰ সংখ্যাৰ বৰ্গতকৈ 4 টা মাৰ্বল কম আছে, অনুপৰ হাতত বিজয়ৰ হাতত থকা মার্বলতকৈ 4 টা মার্বল বেছি আছে, প্রকাশে ক’লে যে তাৰ হাতত নবীন, বিজয় আৰু অনুপৰ হাতত একেলগে থকা মার্বলতকৈ 6 টা মার্বল বেছি আছে। নবীন, বিজয়, অনুপ আৰু প্ৰকাশৰ হাতত থকা মাৰ্বল একেলগ কৰিলে মুঠ মাৰ্বলৰ সংখ্যা বীজগণিতীয় ৰাশিত প্রকাশ কৰা।
উত্তৰঃ ধৰা হ’ল, নবীনৰ হাতত থকা মাৰ্বলৰ সংখ্যা x
∴ বিজয়ৰ হাতত থকা মাৰ্বলৰ সংখ্যা x² – 4
অনুপৰ হাতত থকা মাৰ্বলৰ সংখ্যা (x² – 4) + 4 = x²
প্ৰকাশৰ হাতত থকা মাৰ্বলৰ সংখ্যা = [x + (x² – 4) + x²] + 6
= 2x² + x + 2
∴ নবীন, বিজয়, অনুপ আৰু প্ৰকাশৰ হাতত থকা মাৰ্বলৰ মুঠ সংখ্যা
= x + (x² – 4) + x² + (2x² + x + 2)
= x + x² – 4 + x² + (2x² + x + 2)
= 4x² + 2x – 2
অনুশীলনী – 12.3 |
|---|
1. a = 1 হ’লে তলৰ বীজগণিতীয় ৰাশিবোৰৰ মান নির্ণয় কৰাঃ
(i) 2a + 1
উত্তৰঃ 2a + 1
= 2 × 1 + 1
= 2 + 1
= 3
(ii) a² – 2a + 1
উত্তৰঃ a² – 2a + 1
= 1² – 2 × 1 + 1
= 1 – 2 + 1
= 2 – 5
= 0
(iii) a + 3/4
উত্তৰঃ a + 3/4
= 1 + 3/4
= 4/4
= 1
(iv) 1/2a – 4
উত্তৰঃ 1/2a – 4
= 1/2 × 1 – 4
= 1/2 – 4
= 1 – 8/2
= -7/2
(v) a³ + a² + a – 1
উত্তৰঃ a³ + a² + a – 1
= 1³ + 1² + 1 – 1
= 1 + 1 + 1 – 1
= 3 – 1 – 2
2. x = -3 হ’লে তলৰ বীজগণিতীয় ৰাশিবোৰৰ মান নির্ণয় কৰাঃ
(i) -x² + 4x + 3
উত্তৰঃ -x² + 4x + 3
= -(-3)² + 4(-3) + 3
= -9 – 12 + 3
= -21 + 3
= 18
(ii) 2x² + x + 3
উত্তৰঃ 2x² + x + 3
= 2(-3)² + (-3) + 3
= 2 × 9 – 3 + 3
= 18
(iii) x³ – x² + 1
উত্তৰঃ x³ – x² + 1
= (-3)³ – (-3)² + 1
= -27 – 9 + 1
= -36 + 1
= -35
(iv) 3x + 1
উত্তৰঃ 3x + 1
= 3(-3) + 1
= -9 + 1
= -8
(v) x/3 + 2/3
উত্তৰঃ x/3 + 2/3
= -3/3 + 2/3
= (-3 + 2)/3
= -1/3
3. x = 1 হ’লে আৰু y = -1 হ’লে তলত দিয়া বীজগণিতীয় ৰাশিবোৰৰ মান নির্ণয় কৰাঃ
(i) x² + xy + y²
উত্তৰঃ x² + xy + y²
= 1² + 1 × (-1) + (-1)²
= 1 – 1 + 1
= 1
(ii) x² + y²
উত্তৰঃ x² + y²
= 1² + (-1)²
= 1 + 1
= 2
(iii) x² – y²
উত্তৰঃ x² – y²
= 1² – (-1)²
= 1 + 1
= 2
(iv) x² + y + 1
উত্তৰঃ x² + y + 1
= 1² + (-1)² + 1
= 1 + 1 + 1
= 3
(v) 3x + y
উত্তৰঃ 3x + y
= 3 × 1 + 1(-1)
= 3 – 1
= 2
(vi) x²y + xy² + x
উত্তৰঃ x²y + xy² + x
= 1²(-1) + 1 × (-1)² + 1
= 1(-1) + 1 × 1 + 1
= -1 + 1 + 1
= 1
4. তলৰ ৰাশিসমূহ সৰল কৰা আৰু x = – 2 ৰ বাবে মান নির্ণয় কৰাঃ
(i) x² + x + 7 + x + x² – 1
উত্তৰঃ x² + x + 7 + x + x² – 1
= (-2)² + (-2) + 7 + (-2) + (-2)² – 1
= 4 – 2 + 7 – 2 + 4 – 1
= 15 – 6
= 9
(ii) 3(x + 4) + 2x + 1
উত্তৰঃ 3(x + 4) + 2x + 1
= 3(-2 + 4) + 2(-2) + 1
= 3 × 2 – 4 + 1
= 6 – 4 + 1
= 7 – 4
= 3
(iii) 3x – (2x – 1)
উত্তৰঃ 3x – (2x – 1)
= 3(-2) – [2(-2) – 1]
= -6 – 4 – 1
= -6 – (-5)
= -6 + 5
= -1
(iv) (x² + x) – (2x² – x + 1)
উত্তৰঃ (x² + x) – (2x² – x + 1)
= [(-2)² + (-2)] – [2(-2)² – 2) + 1
= [4 – 2] – [2 × 4 + 2 + 1]
= 2 – (8 + 2 + 1)
= 2 – 11
= -9
(v) x³ + 2x² – x + 2x² + 2x + 1
উত্তৰঃ x³ + 2x² – x + 2x² + 2x + 1
= (-2)³ + 2(-2)² – 2 + 2(-2)² + 2(-2) + 1
= 8 + 2 × 4 + 2 + 2 × 4 – 4 + 1
= -8 + 8 + 2 + 8 – 4 + 1
= 7
(vi) x³ – 4(x – 5)
উত্তৰঃ x³ – 4(x – 5)
= (-2)³ 4(-2 – 5)
= -8 – 4(-7)
= -8 + 28
= 20
5. তলৰ ৰাশিসমূহ সৰল কৰা আৰু মান নির্ণয় কৰা যদি x = 2, y = -3 আৰু z = -10 হয়।
(i) 2x + y – z + 3x – 2y + z
উত্তৰঃ দিয়া আছে, x = 2, y = -3, z = -1
2x + y – z + 3x – 2y + z
= 2 × 2 + (-3) – 1 + 3 × 2 – 2(-3) + (-1)

(ii) xy + yz + 2x
উত্তৰঃ xy + yz + 2x
= 2(-3) + (-3)(-1) + 2 × 2
= -6 + 3 + 4 = 1
(iii) 2x²y + xy²z + 3xyz + 6x²y – 2xy²z – 6xyz
উত্তৰঃ 2x²y + xy²z + 3xyz + 6x²y – 2xy²z – 6xyz
= 2 × 2² × (-3) + 2 × (-3)² × (-1) + 3 × 2 × (-3) × (-1) + 6 × 2² × (-3) – 2 × 2 × (-3)² × (-1) – 6 × 2 × (-3) × (-1)
= 2 × 4 × (-3) + 2 × 9 × (-1) + 6 × (-3) × (-1) + 6 × 4 × (-3) – 4 × 9 × (-1) – 6 × 2 × (-3) × (-1)
= -24 – 18 + 18 – 72 + 36 – 36 = -96
(iv) 5 – 3x + 2y – 7x + 6y + 2 + z
উত্তৰঃ 5 – 3x + 2y – 7x + 6y + 2 + z
= 5 – 3 × 2 + 2 × (-3) – 7 × 2 + 6 × (-3) + 2(-1)
= 5 – 6 – 6 – 14 – 18 + 2
= 7 – 45 = -38
(v) (2x + y + z) – (z – 3y) + (2 + x) – (5 – z)
উত্তৰঃ (2x + y + z) – (z – 3y) + (2 + x) – (5 – z)
= {2 × 2 + (-3) + (-1)} + {(-1) -3(-3)} + (2 + 2) + {5 – (-1)}
= {4 – 3 – 1} + {-1 – 9} + 4 + (5 + 1)
= 0 + (-10) + 4 + 6
= -10 + 10 = 0
6. x = 0 ৰ বাবে যদি x² + 2x – p + 1 ৰ মান 6 হয় তেন্তে pৰ মান নির্ণয় কৰা।
উত্তৰঃ x² + 2x – p + 1 ত x = 0 বহুৱালে পাওঁ,
0² + 2 × 0 – p + 1 = 6
⇒ -p + 1 = 6
⇒ -p = 6 – 1
⇒ -p = 5
⇒ p = -5
অনুশীলনী – 12.4 |
|---|
1. প্রদত্ত বীজগণিতীয় ৰাশিৰ মানৰ তালিকাখন সম্পূৰ্ণ কৰা [অজ্ঞাত ৰাশিৰ সলনি 1, 2, 3… ব্যৱহাৰ কৰা]
|
ৰাশি |
পদসমূহ |
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
প্ৰথম |
দ্বিতীয় |
তৃতীয় |
চতুৰ্থ |
পঞ্চম |
50তম |
…… |
100তম |
||
|
(i) |
5n + 1 |
6 |
11 |
||||||
|
(ii) |
3n – 1 |
2 |
8 |
||||||
|
(iii) |
x² + 1 |
2 |
17 |
||||||
|
(iv) |
2x + 3 |
5 |
9 |
13 |
203 |
||||
|
(v) |
4n – 1 |
3 |
199 |
||||||
উত্তৰঃ
|
ৰাশি |
পদসমূহ |
||||||||
|---|---|---|---|---|---|---|---|---|---|
|
প্ৰথম |
দ্বিতীয় |
তৃতীয় |
চতুৰ্থ |
পঞ্চম |
50তম |
……. |
100তম |
||
|
(i) |
5n + 1 |
6 |
11 |
16 |
21 |
26 |
251 |
501 |
|
|
(ii) |
3n – 1 |
2 |
5 |
8 |
11 |
14 |
149 |
299 |
|
|
(iii) |
x² + 1 |
2 |
5 |
10 |
17 |
26 |
2501 |
1001 |
|
|
(iv) |
2x + 3 |
5 |
7 |
9 |
11 |
13 |
103 |
203 |
|
|
(v) |
4n – 1 |
3 |
7 |
11 |
15 |
19 |
199 |
399 |
|
2. তলত দিয়া চিত্ৰবোৰলৈ মন কৰাঃ
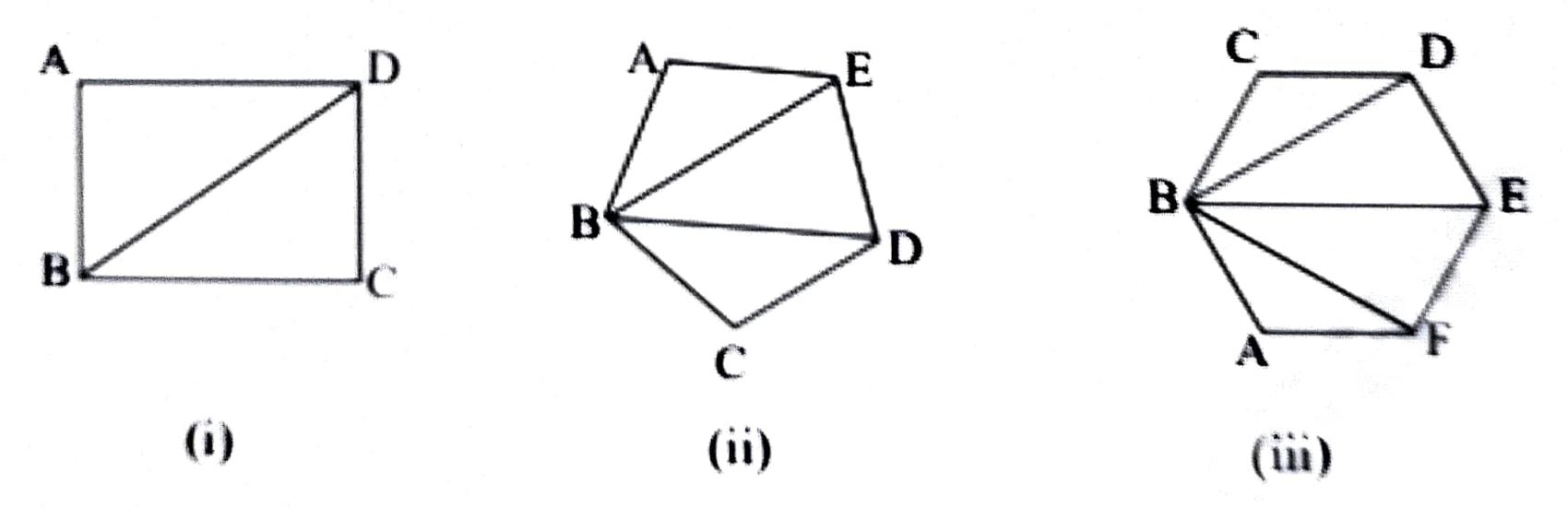
(i) নং চিত্রত ABCD চতুর্ভুজত B শীর্ষ বিন্দুৰ পৰা মাত্র এডাল কর্ণ আঁকিব পাৰি।
(ii) নং চিত্রত ABCDE পঞ্চভুজত B শীর্ষ বিন্দৰ পৰা মাত্র 2 ডাল কর্ণ আঁকিব পাৰি।
(iii) নং চিত্রত ABCDEF ষড়ভুজত B শীর্ষ বিন্দুৰ পৰা মাত্র 3 ডাল কর্ণ আঁকিব পাৰি।
∴ চতুর্ভুজৰ এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 1
পঞ্চভূজৰ এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 2
ষড়ভুজৰ এটা শীর্ঘবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 3
∴ সপ্তভুজত এটা শীর্ষ বিন্দুৰ পৰা কেইটা কৰ্ণ আঁকিব পাৰি?
n বাহুযুক্ত বহুভুজত এটা শীর্ষ বিন্দুৰ পৰা কেইটা কৰ্ণ আঁকিব পাৰি?
উত্তৰঃ চতুর্ভুজৰ এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 4 – 3 = 1
পঞ্চভুজৰ এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 5 – 3 = 2
ষড়ভুজৰ এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 6 – 3 = 3
∴ সপ্তভুজৰ এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = 7 – 3 = 4
n বাহুযুক্ত বহুভুজত এটা শীর্ষবিন্দুৰ পৰা আঁকিব পৰা কৰ্ণৰ সংখ্যা = n – 3
3. তলত দিয়া তালিকা আৰু = 1, 2, 3, 4, 5ৰ বাবে দিয়া মানবোৰ সংখ্যাৰ তলত দিয়া হৈছে। চানেকি সজোৱা (n তম পদটো লিখা।)
(a)
|
n |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
মান |
1 |
4 |
9 |
16 |
? |
চানেকিৰ সাধাৰণ n যুক্ত পদ = ?
উত্তৰঃ
|
n |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
মান |
1 |
4 |
9 |
16 |
25 |
চানেকিৰ সাধাৰণ n যুক্ত পদ = n²
(b)
|
n |
1 |
2 |
3 |
4 |
5 |
– |
n |
|---|---|---|---|---|---|---|---|
|
মান |
4 |
7 |
10 |
13 |
? |
? |
উত্তৰঃ
|
n |
1 |
2 |
3 |
4 |
5 |
– |
n |
|---|---|---|---|---|---|---|---|
|
মান |
4 |
7 |
10 |
13 |
16 |
3n + 1 |
(c)
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
মান |
8 |
10 |
12 |
14 |
16 |
? |
n তম পদ = ?
উত্তৰঃ
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
মান |
8 |
10 |
12 |
14 |
16 |
18 |
n তম পদ = n + (n + 7) = 2n + 6 = 2(n + 6)
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

