SEBA Class 7 Mathematics Chapter 3 – “তথ্যৰ ব্যৱহাৰ” solutions with data handling, graphs, and statistical analysis.
Find SEBA Class 7 Mathematics Chapter 3 – “তথ্যৰ ব্যৱহাৰ” (Data Handling) solutions, designed for Assamese medium students. This chapter covers the basics of data collection, organization, and representation using different methods such as tallies, bar graphs, pictographs, and pie charts.
Students will learn about mean, median, and mode as measures of central tendency, and how to interpret and analyze data effectively. The chapter also introduces probability and real-life applications of data handling in daily life.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students develop strong analytical skills and prepare effectively for exams.
Class 7 Social Science (English Medium) PDF Solutions 2025-26 | SCERT Assam
Get comprehensive solutions, PDFs, and MCQs for SEBA Class 7 Social Science in English Medium. This resource covers Geography, History, and Economics, providing chapter-wise explanations and practice materials to help students excel in their exams.
অনুশীলনী – 3.1 |
|---|
1. প্রথম 10 টা স্বাভাৱিক সংখ্যাৰ গড় আৰু প্ৰসাৰ নিৰ্ণয় কৰা।
উত্তৰঃ প্রথম 10টা স্বাভাৱিক সংখ্যা 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
∴ গড 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10/10
= 55/10 = 5.5
ডাঙৰ সংখ্যা = 10
সৰু সংখ্যা = 1
∴ প্ৰসাৰ = (10 – 1) = 9
2. জিলাভিত্তিক খেল প্রতিযোগিতাত 12 খন বিদ্যালয়ে অংশ গ্রহণ কৰিছিল। প্রতিখন বিদ্যালয়ে লাভ কৰা পদকৰ তালিকা এনে ধৰণৰঃ
11, 8, 13, 6, 10, 15, 18, 9, 10, 9, 11, 12
(i) লাভ কৰা আটাইতকৈ বেছি সংখ্যক পদকৰ সংখ্যা কিমান?
উত্তৰঃ লাভ কৰা আটাইতকৈ বেছি সংখ্যক পদকৰ সংখ্যা = 18
(ii) লাভ কৰা আটাইতকৈ কম সংখ্যক পদকৰ সংখ্যা কিমান?
উত্তৰঃ লাভ কৰা আটাইতকৈ কম সংখ্যক পদকৰ সংখ্যা = 16
(iii) তথ্যখিনিৰ প্ৰসাৰ কিমান?
উত্তৰঃ তথ্যখিনিৰ = প্ৰসাৰ বেছি সংখ্যক পদকৰ সংখ্যা – কম সংখ্যক পদকৰ সংখ্যা = 18 – 6 = 12
(iv) তথ্যখিনিৰ পৰা গড় নির্ণয় কৰা।
উত্তৰঃ তথ্যখিনিৰ গড় = 11 + 8 + 13 + 6 + 10 + 15 + 18 + 9 + 10 + 9 + 11 + 12 +/12 = 132/12 = 11
3. এজন ছাত্রই যোৱা মূল্যায়নত লাভ কৰা নম্বৰৰ তালিকা তলত দিয়া ধৰণৰ (100 নম্বৰৰ ভিতৰত) নম্বৰসমূহৰ গড় নির্ণয় কৰা।
|
গণিত – 75 |
সমাজ বিজ্ঞান – 69 |
|---|---|
|
অসমীয়া – 73 |
ইংৰাজী – 67 |
|
বিজ্ঞান – 82 |
হিন্দী – 78 |
উত্তৰঃ নম্বৰৰ তালিকা
গণিত – 75
অসমীয়া – 73
বিজ্ঞান – 82
সমাজ বিজ্ঞান – 69
ইংৰাজী – 67
হিন্দী – 78
মুঠ বিষয় = 6 টা
মুঠ নম্বৰ = 75 + 73 + 82 + 69 + 67 + 78
= 444
∴ নম্বৰসমূহৰ গড় = 444/6 = 74
4. এখন বিদ্যালয়ৰ যোৱা পাঁচটা বছৰৰ হাইস্কুল শিক্ষান্ত পৰীক্ষাত উত্তীর্ণ হোৱা ছাত্ৰ-ছাত্ৰীৰ সংখ্যা ক্রমে 40, 62, 68, 48, 52 গৰাকী। বিদ্যালয়খনত উত্তীর্ণ হোৱা ছাত্র-ছাত্রীৰ গড় নির্ণয় কৰা।
উত্তৰঃ এখন বিদ্যালয়ৰ পাঁচটা বছৰত হাইস্কুল শিকান্ত পৰীক্ষাত উত্তীর্ণ হোৱা ছাত্ৰ-ছাত্ৰীৰ সংখ্যা ক্রমে 40, 62, 68, 48, 52
∴ উত্তীর্ণ হোৱা ছাত্ৰ-ছাত্ৰীৰ গড় = 40 + 62 + 68 + 48 + 52/5
= 270/5 = 54
5. এজন ক্রিকেট খেলুৱৈয়ে আঠটা ইনিংছত তলত দিয়া ধৰণে স্ক’ৰ কৰেঃ
77, 41, 101, 46, 59, 1, 36, 47 খেলুৱৈজনৰ গড় স্ক’ৰ উলিওৱা।
উত্তৰঃ ক্রিকেট খেলুৱৈজনৰ আঠটা ইনিংছৰ স্ক’ৰ হ’ল– 77, 41, 101, 46, 59, 1, 36, 47
∴ খেলুৱৈজনৰ গড় স্ক’ৰ = 77 + 41 + 101 + 46 + 59 + 1 + 36 + 47/8
= 407/8 = 50.875
6. 7 জন ল’ৰাৰ ওজন ক্রমে 36, 32, 30, 28, 32, 33, 26 কি.গ্রা।
(i) ল’ৰা কেইজনৰ ওজনৰ গড় নির্ণয় কৰা।
উত্তৰঃ ল’ৰাকেইজনৰ ওজনৰ গড় = 36 + 32 + 30 + 28 + 32 + 33 + 26/7
= 217/7 = 31
(ii) 30 কি. গ্রাতকৈ বেছি ওজনৰ কিমানজন ল’ৰা আছে?
উত্তৰঃ 30 কি.গ্রামতকৈ বেছি ওজনৰ ল’ৰাৰ সংখ্যা = 36 + 32 + 32 + 33
= 133 জন।
(iii) 25 কি.গ্রাতকৈ কম ওজনৰ ল’ৰা ওপৰৰ তালিকাত আছেনে? যদি আছে কিমানজন আছে?
উত্তৰঃ 25 কি.গ্রামতকৈ কম ওজনৰ ল’ৰা নাই।
7. মীৰাই তেওঁলোকৰ আত্মসহায়ক গোটত যোৱা পাঁচটা মাহত 500 টকা, 600 টকা, 600 টকা, 700 টকা আৰু 500 টকাকৈ সঞ্চয় কৰিলে। তেওঁব প্রতিমাহত গড় সঞ্চয় কিমান?
উত্তৰঃ মীৰাই 5 টা মাহত সঞ্চয় কৰা মুঠ টকা
= (500 + 600 + 600 + 700 + 500) = 2900 টকা
∴ মীৰাৰ গড় সঞ্চয় = 2900/5 = 580 টকা।
৪. প্রাথমিক বিদ্যালয় এখনৰ শ্রেণীসমূহব ছাত্র-ছাত্রীৰ সংখ্যা তলত দিয়া ধৰণৰঃ
|
প্ৰথম |
দ্বিতীয় |
তৃতীয় |
চতুৰ্থ |
পঞ্চম |
|---|---|---|---|---|
|
26 |
32 |
34 |
28 |
30 |
(i) বিদ্যালয়খনৰ শ্রেণীসমূহত ছাত্র-ছাত্রীৰ গড় সংখ্যা নির্ণয় কৰা।
উত্তৰঃ শ্রেণীসমূহত ছাত্র-ছাত্ৰীৰ গড় সংখ্যা = মুঠছাত্ৰ-ছাত্ৰীৰসংখ্যা/শ্রেণীৰসংখ্যা
= 26 + 32 + 34 + 28 + 30/5
= 150/5 = 30 জন।
(ii) প্রথম সাময়িকীৰ পিছত দ্বিতীয় আৰু পঞ্চম শ্রেণীত ক্রমে 3 জন আৰু 2 জন ছাত্র-ছাত্রীয়ে নতুনকৈ নামভর্তি কৰিলে। তেতিয়া বিদ্যালয়ৰ শ্রেণীসমূহত ছাত্র-ছাত্রীৰ সংখ্যাৰ নতুন গড় নির্ণয় কৰা।
উত্তৰঃ প্রথম সাময়িকীৰ পিছত ছাত্ৰ-ছাত্ৰীৰ গড় সংখ্যা = 26 + (32 + 3) + 34 + 28 + (30 + 2)/5
= 26 + 35 + 34 + 28 + 32/5 = 155/5 = 31 জন।
|
অনুশীলনী – 3.2 |
|---|
1. তলৰ তথ্যখিনিৰ পৰা বহুলক নিৰ্ণয় কৰাঃ
(i) 2, 2, 3, 3, 4, 4, 5, 5, 5, 6, 6, 7, 7
উত্তৰঃ তথ্যখিনিৰ পৰা 5 আটাইতকৈ বেছি অৰ্থাৎ 3 বাৰ পোৱা গৈছে।
∴ বহুলক = 5
(ii) 41, 43, 41, 46, 47, 48, 41, 49, 49
উত্তৰঃ তথ্যখিনিৰ 41 আটাইতকৈ বেছি অৰ্থাৎ 3 বাৰ পোৱা গৈছে।
∴ বহুলক = 41
2. প্রাপ্ত নম্বৰৰ বহুলক নিৰ্ণয় কৰা (20 নম্বৰৰ ভিতৰত):
|
ছাত্ৰ-ছাত্ৰীৰ সংখ্যা |
3 |
3 |
4 |
7 |
4 |
2 |
|---|---|---|---|---|---|---|
|
প্ৰাপ্ত নম্বৰ |
10 |
11 |
12 |
13 |
14 |
15 |
উত্তৰঃ তথ্যখিনিৰ 13 নম্বৰ আটাইতকৈ বেছি ছাত্র-ছাত্রীয়ে লাভ কৰিছে
∴ নির্ণয় বহুলক = 13
3. তলৰ তথ্যখিনিৰ পৰা মধ্যমা নিৰ্ণয় কৰাঃ
(i) 2, 0, 1, 5, 3, 4, 6, 2, 9, 10
উত্তৰঃ তথ্যখিনি উর্ধক্রমত সজালে পাওঁ, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12,
ইয়াত মুঠ ৰাশি 11 টা
∴ মধ্যমা = 11 + 1/2 = 12/6 = 6 তম ৰাশি, অর্থাত 5
(ii) 9, 7, 8, 11, 12, 9, 8, 12, 10, 9
উত্তৰঃ তথ্যখিনি উর্ধক্রমত সজালে পাওঁ, 5, 7, 8, 8, 9, 9, 9, 10, 11, 12, 12
∴ মধ্যমা = (11 + 1)/2 = 12/6 = 6 তম ৰাশি, অৰ্থাৎ 9
4. 17 জন ছাত্র-ছাত্রীয়ে গণিতৰ মূল্যায়ণ (50 নম্বৰ ভিতৰত) পোৱা নম্বৰ তালিকা তলত দিয়া ধৰণৰঃ 28, 32, 35, 21, 27, 35, 27, 42, 35, 22, 23, 35, 25, 23, 40, 24, 31 এই তথ্যখিনিৰ পৰা বহুলক আৰু মধ্যমা নির্ণয় কৰা। দুয়োটা মান একেইনে?
উত্তৰঃ গণিতৰ মূল্যায়নখিনি উৰ্ধক্ৰমত সজালে পাওঁ
21, 22, 23, 23, 24, 25, 27, 27, 28, 31, 32, 35, 35, 35, 35, 40, 42
ইয়াক বহুলক 35 [∴ আটাইতকৈ বেছি 4 বাৰ আছে]
মধ্যমা = (17 + 1)/2 = 9 তম ৰাশি, অৰ্থাৎ, 28
দুয়োটা মান একে নহয়।
5. তলৰ তথ্যসমূহব পৰা বহুলক আৰু মধ্যমা নির্ণয় কৰা আৰু দুয়োটা মান একে হয়নে?
13, 16, 12, 14, 19, 12, 14, 13, 14
উত্তৰঃ তথ্যসমূহ উর্ধক্রমত লিখিলে পাওঁ,
12, 12, 13, 13, 14, 14, 16, 19
∴ বহুলক 14 [14 = 3 টা]
মধ্যমা = (9 + 1)/2 = 10/2 = 5 তম তথ্য, অৰ্থাৎ, 14
দুয়োটা মান একে।
6. এটা শ্রেণীৰ 13 জন ছাত্র-ছাত্রীৰ বয়স (বছৰৰ হিচাপত) তলত দিয়া ধৰণৰঃ
14, 14, 15, 14, 14, 14, 15, 14, 14, 15, 15, 14, 14
তথ্যসমূহৰ পৰা মধ্যমান, বহুলক আৰু মধ্যমা নির্ণয় কৰা।
উত্তৰঃ ছাত্ৰ-ছাত্ৰীৰ বয়স উর্ধক্ৰমত,
14, 14, 14, 14, 14, 14, 14, 14, 15, 15, 15, 15
∴ মধ্যমান, = 14 + 14 + 14 + 14 + 14 + 14 + 14 + 14 + 15 + 15 + 15 + 15/13
= 186/13 = 14.31 (প্রায়)
ইয়াত, 14, 9 বাৰ পোৱা গৈছে আৰু 15, 4 বাৰ পোৱা গৈছে।
∴ বহুলক 14
মধ্যমা = (13 + 1)/2 = 14/2 = 7 তম পদ অৰ্থাৎ 14
7. তলৰ তালিকাখন পূৰ কৰাঃ
|
নম্বৰ |
প্ৰসাৰ |
মধ্যমান |
বহুলক |
মধ্যমা |
|---|---|---|---|---|
|
35, 15, 0, 40, 20, 25, 45, 10, 30, 5, 15 |
? |
? |
? |
? |
উত্তৰঃ
|
নম্বৰ |
প্ৰসাৰ |
মধ্যমান |
বহুলক |
মধ্যমা |
|---|---|---|---|---|
|
35, 15, 0, 40, 20, 25, 45, 10, 30, 5, 15 |
45 |
21.5 |
15 |
20 |
৪. তলৰ উক্তিবোৰ শুদ্ধ নে অশুদ্ধ কোৱাঃ
(i) বহুলক সদায় তথ্যৰ মাজত থকা এটা ৰাশি।
উত্তৰঃ সত্য।
(ii) মধ্যমান সদায় তথ্যৰ মাজত থকা এটা ৰাশি।
উত্তৰঃ সত্য।
(iii) মধ্যমা সদায় তথ্যৰ মাজত থকা এটা ৰাশি।
উত্তৰঃ অসত্য।
9. তলৰ তথ্যসমূহৰ মধ্যমান, বহুলক আৰু মধ্যমা নির্ণয় কৰাঃ
(i) 8, 8, 8, 8, 18, 18, 18, 18, 18
উত্তৰঃ প্রদত্ত তথ্যৰ মধ্যমান = 8 + 8 + 8 + 8 + 18 + 18 + 18 + 18 + 18/9 = 13.5
ইয়াত, 8, 4 বাৰ আৰু 18, 5 বাৰ আছে।
∴ বহুলক = 18
প্রদত্ত তথ্যত 18 ৰাশিটো একেবাৰে মাজত আছে।
∴ নির্ণেয় মধ্যমা = 18
(ii) 3, 10, 10, 12, 14, 16, 16, 18, 18, 25, 28
উত্তৰঃ প্রদত্ত তথ্যৰ মধ্যমান = 3 + 10 + 10 + 12 + 14 + 16 + 16 + 18 + 18 + 25 + 28/11 = 15.45
ইয়াত, 10, 2 বাৰ 16, 2 বাৰ আৰু 18, 2 বাৰ আছে।
∴ বহুলক = 10, 12 আৰু 18
প্রদত্ত তথ্যত 16 ৰাশিটো একেবাৰে মাজত আছে।
∴ নির্ণেয় মধ্যমা = 16
(iii) 23, 2, 42, 6, 36, 11, 29, 9, 15
উত্তৰঃ প্রদত্ত তথ্যৰ মধ্যমান = 23 + 2 + 42 + 6 + 36 + 11 + 29 + 9 + 15/9 = 19.2
∴ বহুলক = 36
প্রদত্ত তথ্যত 36 ৰাশিটো একেবাৰে মাজত আছে।
∴ নির্ণেয় মধ্যমা = 36
অনুশীলনী – 3.3 |
|---|
1. দণ্ডচিত্ৰৰ সহায়ত প্রশ্নবোৰৰ উত্তৰ লিখা।
(a) এখন বিদ্যালয়ৰ বিভিন্ন খেল ভালপোৱা ছাত্র-ছাত্রীৰ সংখ্যা দণ্ডলেখৰ সহায়ত দেখুওৱা হৈছে। লেখটো অধ্যয়ন কৰি তলৰ প্রশ্নবোৰৰ উত্তৰ উলিওৱা।
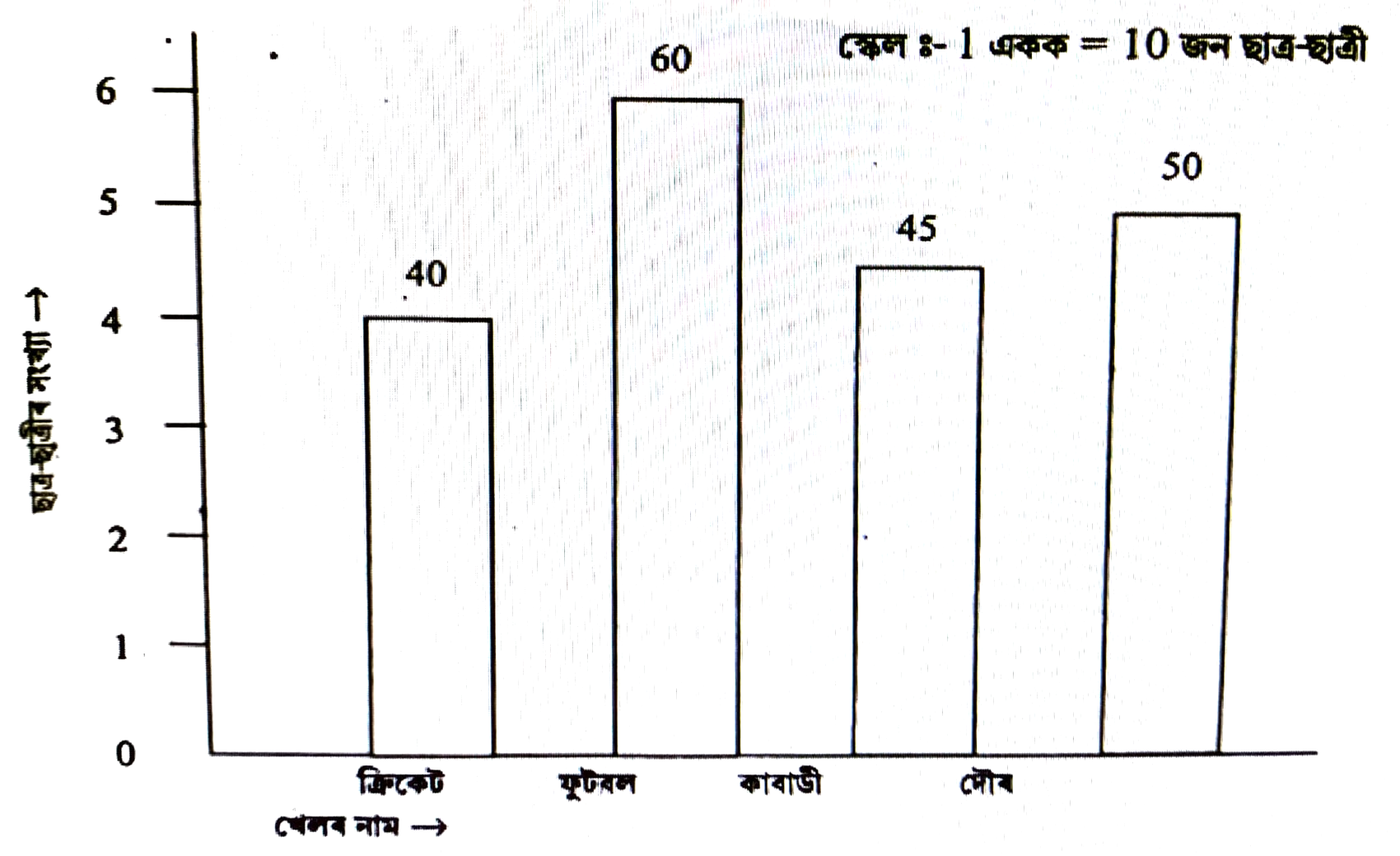
(i) কিমান গৰাকী ছাত্ৰ-ছাত্ৰীয়ে ফুটবল ভাল পায়?
উত্তৰঃ 60 গৰাকীয়ে।
(ii) চাৰিওবিধ খেল ভালপোৱা মুঠ ছাত্ৰ-ছাত্ৰীৰ সংখ্যা কিমান?
উত্তৰঃ 40 + 60 + 45 + 50 = 195
(iii) আটাইতকৈ বেছি আৰু আটাইতকৈ কম ভালপোৱা খেল দুবিধৰ মাজত ছাত্র-ছাত্ৰীৰ পাৰ্থক্য কিমান?
উত্তৰঃ আটাইতকৈ বেছি আৰু আটাইতকৈ কম ভালপোৱা খেল দুবিধৰ মাজত ছাত্র-ছাত্ৰীৰ পাৰ্থক্য (60 – 40 = 20)
(b) গণিতৰ পৰীক্ষাত 60, 65, 70, 75, 80 (100 নম্বৰৰ ভিতৰত) এই নম্বৰসমূহ লাভ কৰা ছাত্র-ছাত্রীৰ সংখ্যা দণ্ডচিত্ৰৰ সহায়ত দেখুওৱা হৈছে।
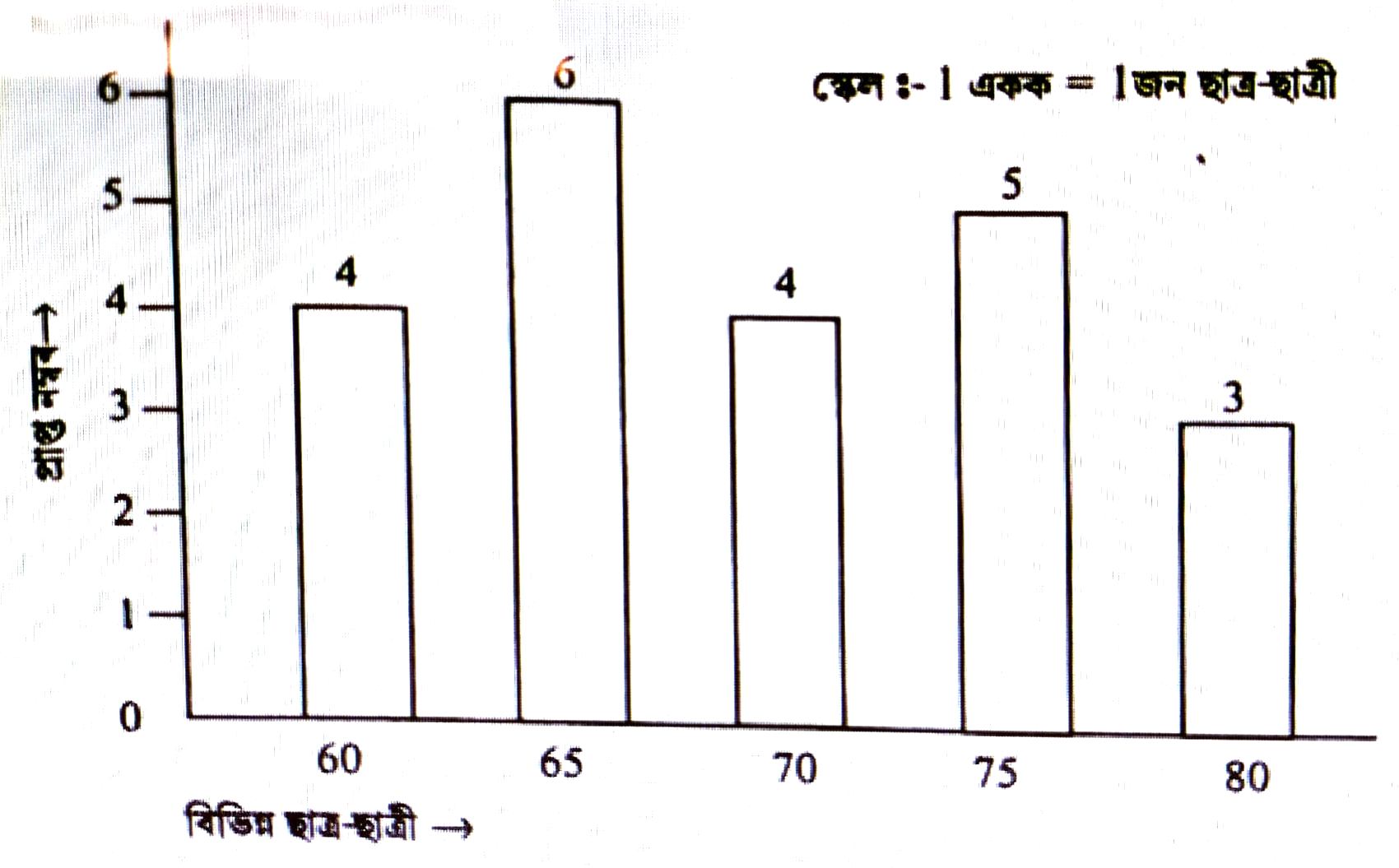
(i) কিমানজন ছাত্র-ছাত্রীয়ে 70 তকৈ বেছি নম্বৰ লাভ কৰিছে?
উত্তৰঃ 4 + 5 + 3 = 12 জন ছাত্র-ছাত্রীয়ে।
(ii) কেইজন ছাত্র-ছাত্রীয়ে সমান নম্বৰ লাভ কৰিছে আৰু কিমান?
উত্তৰঃ 60 আৰু 70 নম্বৰ লাভ কৰিছে 4 জনকৈ ছাত্র-ছাত্রীয়ে।
(iii) 65 আৰু 75 – এই নম্বৰ দুটা লাভ কৰা মুঠ ছাত্ৰ-ছাত্ৰীৰ সংখ্যা কিমান?
উত্তৰঃ 6 + 5 = 11 জন ছাত্র-ছাত্রীয়ে।
2. সাঁতোৰৰ প্ৰশিক্ষণ কেন্দ্র এটাত যোৱা পাঁচটা বছৰত নামভৰ্তি কৰা প্ৰশিক্ষাৰ্থীৰ সংখ্যা তলত দিয়া ধৰণৰ–
|
বছৰ |
2014 |
2015 |
2016 |
2017 |
2018 |
|---|---|---|---|---|---|
|
প্ৰশিক্ষাৰ্থীৰ সংখ্যা |
650 |
700 |
450 |
500 |
600 |
উপযুক্ত স্কেল ব্যৱহাৰ কৰি এটা দণ্ডলেখ প্রস্তুত কৰা আৰু লগতে তলৰ প্ৰশ্নসমূহৰ উত্তৰ দিয়া–
(i) আটাইতকৈ বেছি প্রশিক্ষার্থী কোনটো বছৰত আছে?
(ii) 2014, 2015 আৰু 2016 এই তিনিওটা বছৰত নামভৰ্ত্তি কৰা মুঠ প্রশিক্ষার্থীৰ সংখ্যা কিমান?
উত্তৰঃ
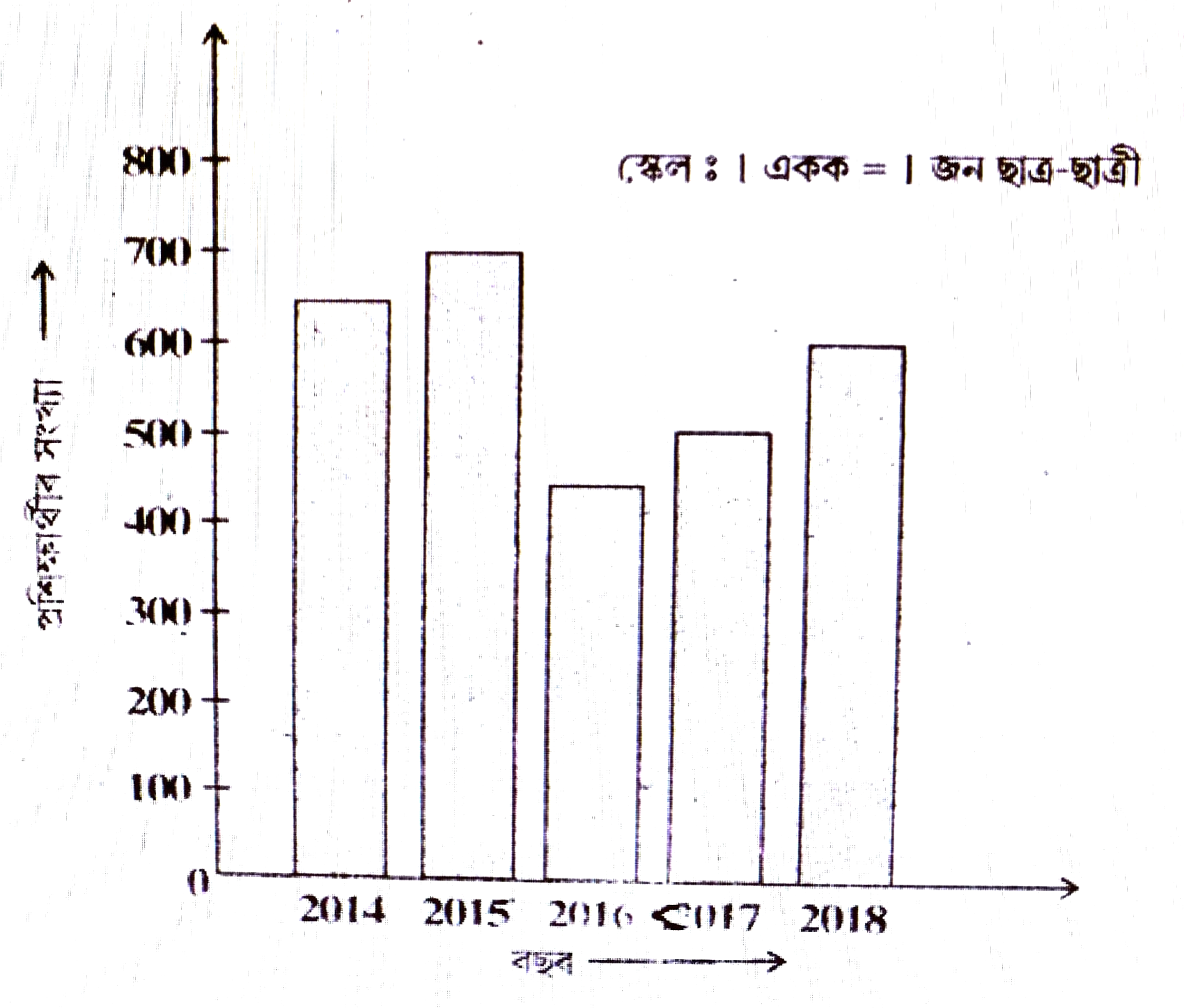
(i) আটাইতকৈ বেছি প্ৰশিক্ষাৰ্থীৰ 2015 চনত আছে।
(ii) 2014, 2015 আৰু 2016 ৰ নামভৰ্তি কৰা মুঠ প্ৰশিক্ষাৰ্থীৰ সংখ্যা = 650 + 700 + 450 = 1800 জন।
3. তলত বিভিন্ন ৰং ভালপোৱা আৰু বেয়া পোৱা ছাত্র-ছাত্রীৰ এখন তালিকা প্রস্তুত কৰা হ’ল–
|
ৰঙৰ নাম |
নীলা |
সেউজীয়া |
ৰঙা |
বেঙুনীয়া |
|---|---|---|---|---|
|
ভাল পোৱা ছাত্ৰ-ছাত্ৰীৰ সংখ্যা |
14 |
15 |
12 |
14 |
|
বেয়া পোৱা ছাত্ৰ-ছাত্ৰীৰ সংখ্যা |
7 |
10 |
6 |
5 |
উপযুক্ত স্কেল ব্যৱহাৰ কৰি উক্ত তথ্যৰ পৰা দ্বৈত দণ্ডলেখ অংকন কৰা।
উত্তৰঃ
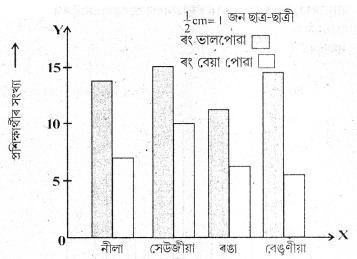
4. এজন ছাত্রই ষষ্ঠ আৰু সপ্তম শ্ৰেণীৰ চাৰিওটা মূল্যায়ণত 200 নম্বৰ ভিতৰত লাভ কৰা নম্বৰসমূহ তলত দিয়া হ’ল। উপযুক্ত স্কেল ব্যৱহাৰ কৰি এটা দ্বৈত দণ্ডলেখ অংকন কৰা আৰু তলৰ প্রশ্নবোৰৰ উত্তৰ দিয়া।
|
শ্ৰেণী |
ইংৰাজী |
গণিত |
বিজ্ঞান |
অসমীয়া |
সমাজ বিজ্ঞান |
|---|---|---|---|---|---|
|
ষষ্ঠ |
144 |
164 |
160 |
134 |
170 |
|
সপ্তম |
130 |
175 |
170 |
165 |
150 |
(i) কোনটো বিষয়ত ছাত্রজনে আটাইতকৈ উন্নত ফল দেখুৱাইছে?
(ii) কোনটো বিষয়ৰ কৃতকার্যতাৰ স্তৰ একেবাৰে নিম্ন।
(iii) সৰ্বাধিক নম্বৰ পোৱা বিষয় আৰু শ্রেণীটো কি?
উত্তৰঃ
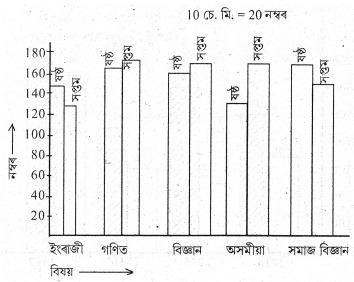
(i) গণিত বিষয়ত ছাত্রজনে আটাইতকৈ উন্নত ফল দেখুৱাইছে।
(ii) ইংৰাজী বিষয়ৰ কৃতকাৰ্যতাৰ স্তৰ একেবাৰে নিম্ন।
(iii) সৰ্বাধিক নম্বৰ পোৱা বিষয় হ’ল গণিত আৰু শ্ৰেণীটো সপ্তম।
5. এখন কিতাপৰ দোকানত চাৰিটা বছৰত বিক্ৰী হোৱা ইংৰাজী আৰু অসমীয়া কিতাপৰ সংখ্যা তলত দিয়া হ’ল। তালিকাখনৰ পৰা উপযুক্ত স্কেল ব্যৱহাৰ কৰি দ্বৈত দণ্ডলেখ অংকন কৰা আৰু প্ৰশ্নবোৰৰ উত্তৰ দিয়া।
|
বছৰ |
2014 |
2015 |
2016 |
2017 |
|---|---|---|---|---|
|
ইংৰাজী |
350 |
400 |
300 |
600 |
|
অসমীয়া |
500 |
600 |
450 |
650 |
(i) আটাইতকৈ বেছি অসমীয়া কিতাপ কোনটো চনত বিক্রী হৈছিল?
(ii) 2016 চনত বিক্ৰী হোৱা অসমীয়া আৰু ইংৰাজী কিতাপৰ পাৰ্থক্য কিমান?
(iii) 2015 চনত মুঠ কিমান কিতাপ বিক্রী হৈছিল?
উত্তৰঃ
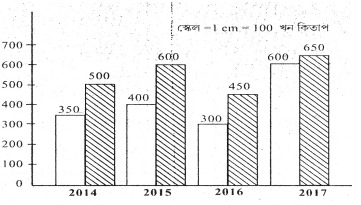
(i) 2017 চনত।
(ii) পার্থক্য = 450 – 300 = 150
(iii) 400 + 600 = 1000 খন।
অনুশীলনী – 3.4 |
|---|
1. তলত দিয়াবোৰ নিশ্চিতভাৱে ঘটিব, ঘটনাটো অসম্ভৱ, ঘটিব পাৰে কিন্তু নিশ্চিত নহয় কোনটো শুদ্ধ কোৱা?
(i) অহা বছৰ স্বাধীনতা দিৱস 15 আগষ্টত উদযাপন কৰা হ’ব।
উত্তৰঃ নিশ্চিতভাৱে ঘটিব।
(ii) তুমি ভাল ৰিজাল্ট কৰিলে এটা পুৰস্কাৰ পাবা।
উত্তৰঃ ঘটিব পাৰে কিন্তু নিশ্চিত নহয়।
(iii) অহা সপ্তাহত বুধবাৰৰ পিছৰ দিনটো শুক্রবাৰ হ’ব।
উত্তৰঃ ঘটনাটো অসম্ভৱ।
(iv) তোমাক আজি বন্ধুজনে দেখা কৰিব।
উত্তৰঃ ঘটিব পাৰে কিন্তু নিশ্চিত নহয়।
(v) তুমি চিৰিয়াখানালৈ গ’লে ডাইন’চৰ দেখা পাবা।
উত্তৰঃ ঘটনাটো অসম্ভৱ।
2. এটা পাত্ৰত চাৰিটা মাৰ্বল আছে। এটা ৰঙা, এটা হালধীয়া, এটা কলা আৰু এটা বগা ৰঙৰ।
(i) ৰঙা ৰঙৰ মাৰ্বলটো উলিয়াই অনাৰ সম্ভাৱিতা কিমান?
উত্তৰঃ ৰঙা মাৰ্বলটো উলিয়াই অনাৰ সম্ভাৱিতা = ৰঙামাৰ্বলৰসংখ্যা/মুঠমাৰ্বলৰসংখ্যা = 1/4
(ii) বগা ৰঙৰ মাৰ্বলটো উলিয়াই অনাৰ সম্ভাৱিতা কিমান?
উত্তৰঃ বগা মার্কলটো উলিয়াই অনাৰ সম্ভাৱিতা = বগামাৰ্বলৰসংখ্যা/মুঠমাৰ্বলৰসংখ্যা = 1/4
3. ৰীতা, ববিতা, হেমা, পুষ্পা আৰু মেঘাই নিজৰ নিজৰ নামবোৰ কাগজৰ টুকুৰাত লিখি এটা বাকচত ভৰালে। মেঘাই বাকচৰ পৰা এটা নাম উলিয়ালে। তাই নিজৰ নামটো উলিয়াই অনাৰ সম্ভাৱিতা কিমান হ’ব?
উত্তৰঃ মুঠ নামৰ সংখ্যা = 5
মেঘাৰ নাম থাকিব = 1 টুকুৰাত
মেঘাই নিজৰ নাম উলিয়াই অনাৰ সম্ভাৱিতা = মেঘানামৰসংখ্যা/মুঠনামৰসংখ্যা = 1/5
4. ‘EDUCATION’ এই শব্দটোৰ পৰা ইংৰাজী স্বৰবৰ্ণখিনি উলিয়াই অনাৰ সম্ভাৱিতা কিমান?
উত্তৰঃ ‘EDUCATION’ শব্দটোত থকা বৰ্ণৰ সংখ্যা = 9
শব্দটোত থকা স্বৰবৰ্ণৰ সংখ্যা = 5
∴ শব্দটোৰ পৰা স্বৰবৰ্ণ উলিয়াই অনাৰ সম্ভাৱিতা = স্বৰবৰ্ণৰসংখ্যা/মুঠবৰ্ণৰসংখ্যা।
= 5/9
5. এটা পাচিত 4 টা আম, 3 টা নাচপতি আৰু 5 টা কল আছে। পাচিটোৰ পৰা গোটেইখিনি কল উলিয়াই অনাৰ সম্ভাৱিতা কিমান হ’ব?
উত্তৰঃ পাচিটোত থকা মুঠ ফলৰ সংখ্যা = 4 + 3 + 5 = 12
শাৰীটোত থকা কলৰ সংখ্যা = 5
∴ পাচিটোৰ পৰা গোটেইখিনি কল উলিয়াই অনাৰ সম্ভাৱিতা = পাচিতধকাকলৰসংখ্যা/মুঠডসৰসংখ্যা = 5/12
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

