Find SEBA Class 7 Mathematics Chapter 7 – “ত্রিভুজৰ সৰ্বাংগসমতা” (Congruence of Triangles) solutions, designed for Assamese medium students. This chapter explains the concept of congruence, its criteria, and how two triangles can be proved congruent.
Students will learn about different congruence criteria such as SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), and RHS (Right Angle-Hypotenuse-Side). The chapter also covers real-life applications of congruent triangles in construction and design.
Our solutions include NCERT-based textbook answers, multiple-choice questions (MCQs), and a detailed chapter summary to help students understand and apply congruence concepts effectively.
To access solutions for all chapters, Click Here
Class 7 Maths (গণিত) PDF Solutions 2025-26 | SCERT Assam
SCERT Assam Class 7 Mathematics PDF Solutions (Assamese Medium) – Get chapter-wise, SEBA-aligned PDF solutions with textbook answers, MCQs, and short questions for easy exam preparation. Download now!
অনুশীলনী – 7.2
1. চিত্ৰত ত্রিভুজৰ যোৰসমূহৰ জোখবোৰ দিয়া আছে। দেখুওৱা যে ত্রিভুজৰ যোৰবোৰ সৰ্বাংগসম। সর্বাংগসমতাৰ চৰ্ত উল্লেখ কৰা।
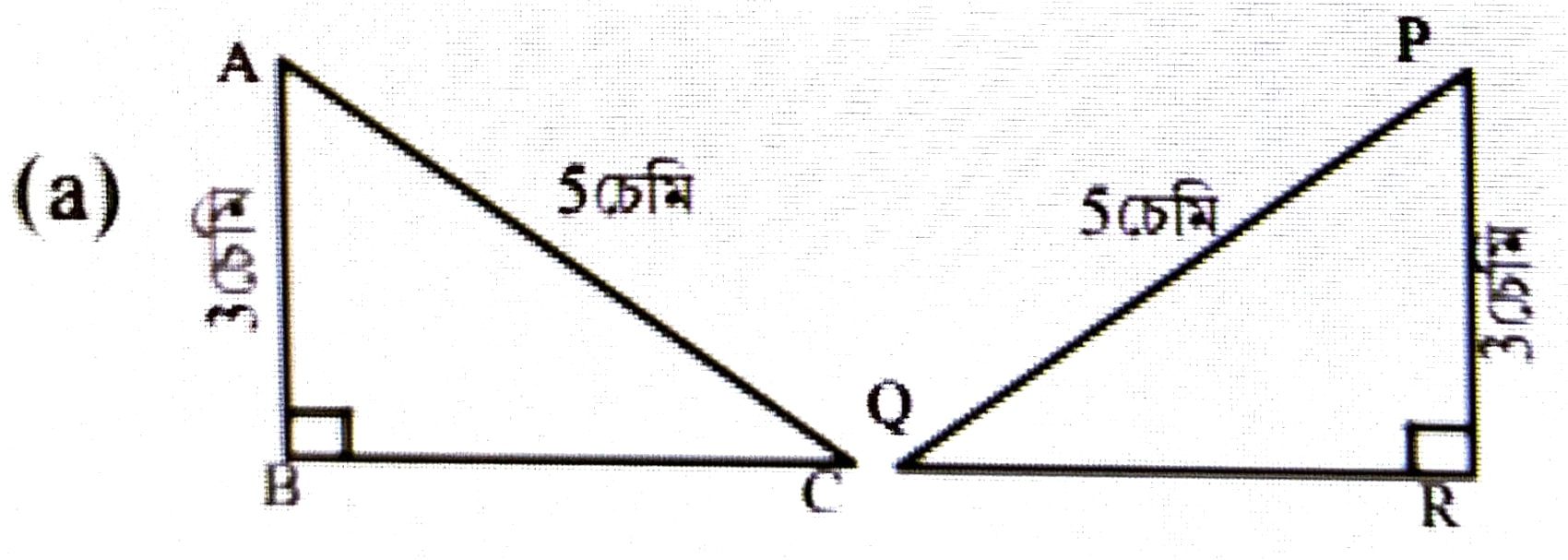
উত্তৰঃ RHS.
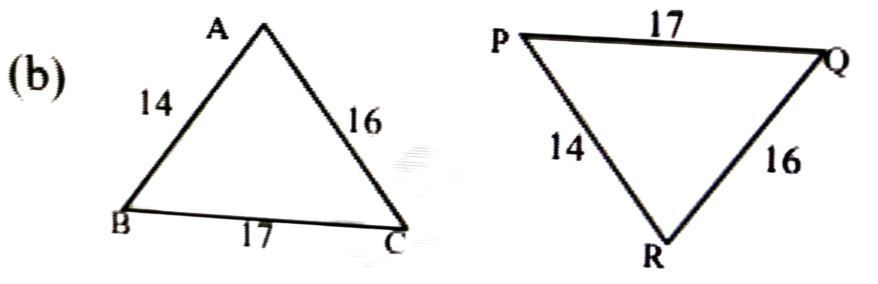
উত্তৰঃ SSS.
(c)
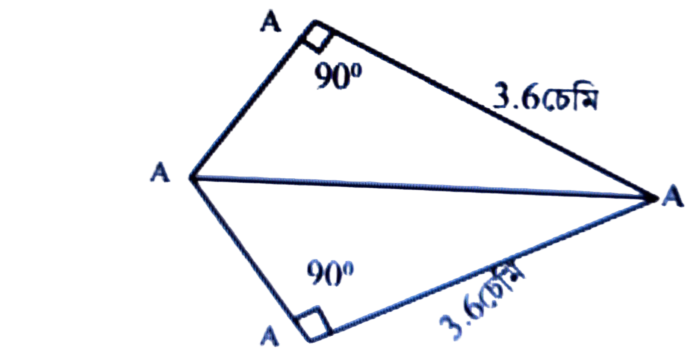
উত্তৰঃ RHS.
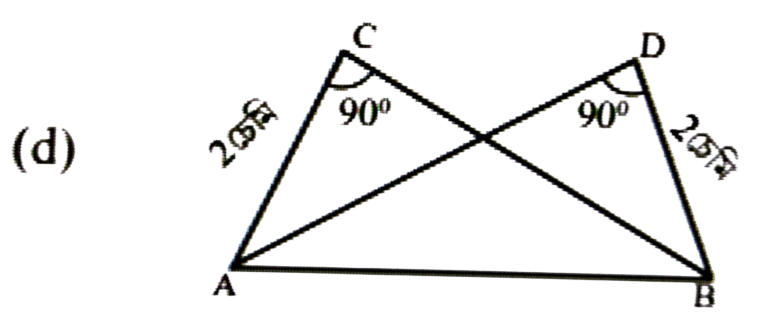
উত্তৰঃ RGS.
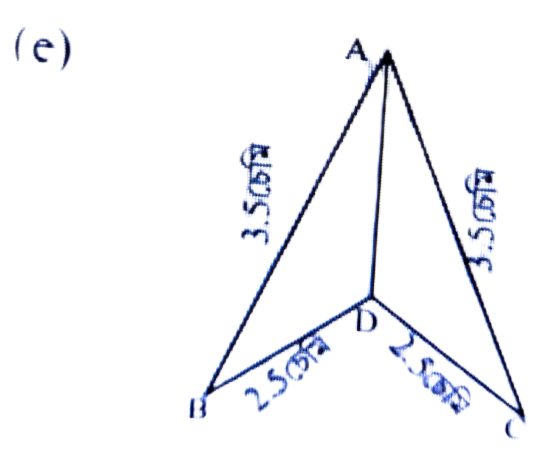
উত্তৰঃ SSS.

উত্তৰঃ SAS.

উত্তৰঃ AAS.
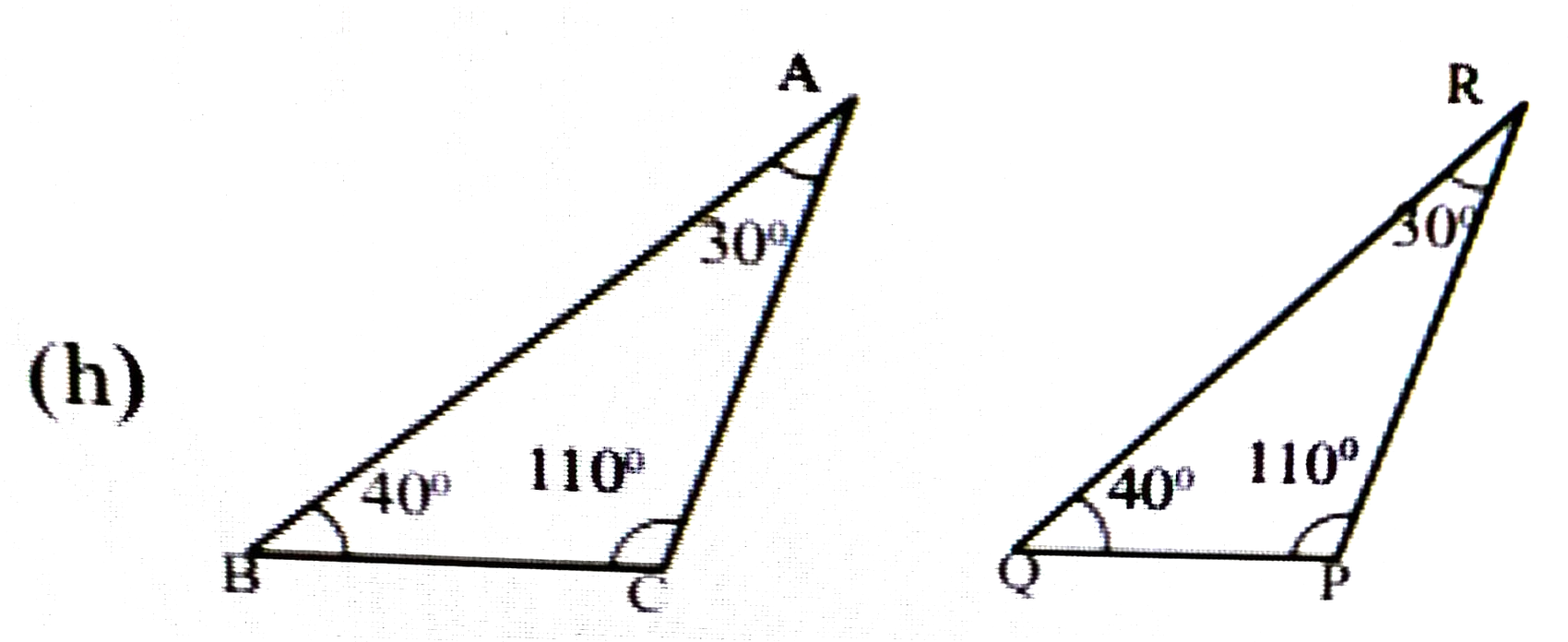
উত্তৰঃ AAS বা ASA.
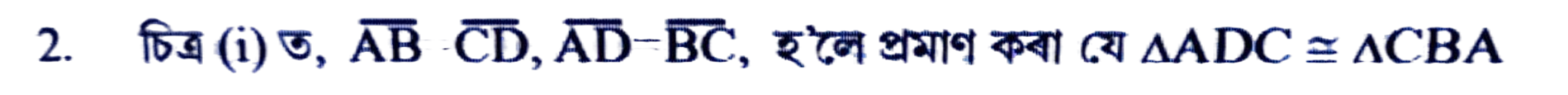

উত্তৰঃ
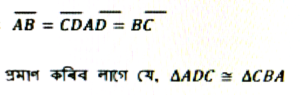
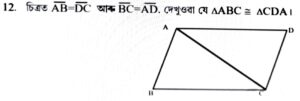
প্রমাণ: ∆ADC আৰু ∆CBA ৰ
AB = CD [দিয়া আছে]
AD – BC [দিয়া আছে]
BC [সাধাৰণ বাহু]
![]()


উত্তৰঃ
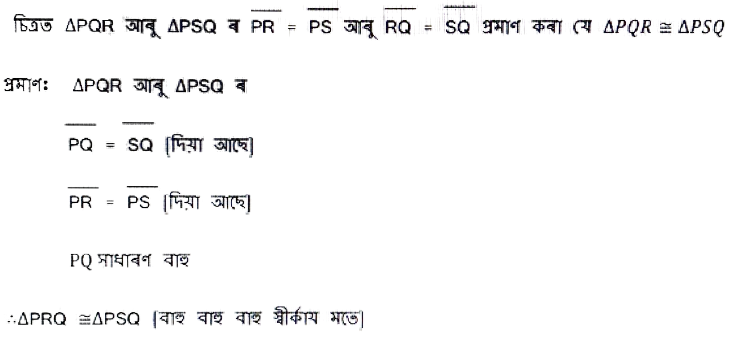
![]()
উত্তৰঃ
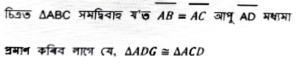
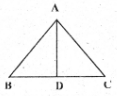
প্ৰমাণঃ ∆ADG আৰু ∆ACD
AB = AC [দিয়া আছে]
BD = CD [∴ D, BC ৰ মধ্যবিন্দু]
AD সাধাৰণ বাহু
![]()
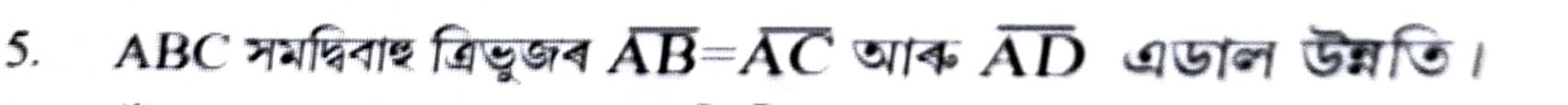
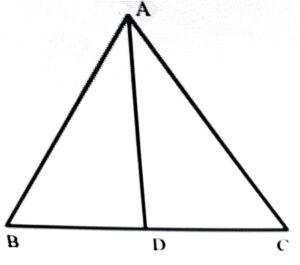
(i) ∆ADB আৰু ∆ADC ৰ তিনিটা সমান অংশ লিখা।
উত্তৰঃ

(ii) ΔΑΒD = AADC হয়নে? কাৰণ দৰ্শোৱা।
উত্তৰঃ

(iii) ∠B = ∠C হ’বনে?
উত্তৰঃ ∠B = ∠C হ’ব, কিয়নো AB = AC
(iv) BD = CD হ’বনে? যুক্তি।
উত্তৰঃ
![]()
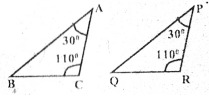
6. ΔАВС ৰ ∠A = 30°, ∠C = 110° আৰু ΔPQR ৰ ∠P = 30°, ∠R = 110°। ΔABC ≅ ΔPQR (কোণ-বাহু-কোণ সর্বাংগসমতাৰ চৰ্ত অনুযায়ী) হয়নে?
উত্তৰঃ ∆ABC ৰ ∠A = 30°, ∠B = 110°
∆PQR ৰ ∠P = 30°, ∠R = 110°
আৰু ∠A = ∠P
![]()

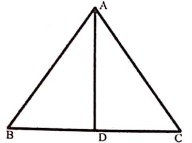
উত্তৰঃ AD য়ে ∠A ক সমদ্বিখণ্ডিত কৰে।
আকৌ, ∆ABC ৰ AB = AC
প্ৰমাণ কৰিব লাগে যে ∠B = ∠C
প্রমাণ: ∆ABD আৰু ∆ACD ৰ
AB = AC [দিয়া আছে]
∠BAD = ∠CAD [দিয়া আছে]
AD সাধাৰণ বাহু
∴ ∆ABD ≌ AACD [বাহু-কোণ-বাহু স্বীকার্য]
∴ ∠B = ∠C [C.P.C.T]

উত্তৰঃ
![]()
![]()
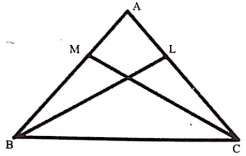
প্রমাণ: ∆ABL আৰু ∠ACM ৰ
AB = AC [∴ ∠B = ∠C]
∠ABL = ∠ACM
[∴ ∠B = ∠C ⇒ ∠B/2 = ∠C/2 ⇒ ∠ABL = ∠ACM]
∠A সাধাৰণ কোণ।
∴ ∆ABC ≌ AACM [কোণ-বাহু-কোণ স্বীকার্য)
![]()
9. ∆ABC ৰ ভূমি BC ৰ মধ্যবিন্দু M বাকী দুটা বাহুৰ পৰা সমদূৰৱৰ্তী। দেখুওৱা যে ত্রিভুজ ABC সমদ্বিবাহু।
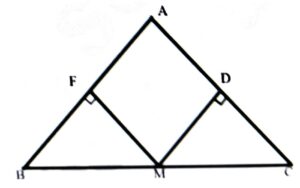
উত্তৰঃ ∆ABC ৰ ভূমি BC ৰ মধ্যবিন্দু M বাকী দুটা বাহুৰ পৰা সমদূৰৱৰ্তী। দেখুওৱা যে ত্রিভুজ ABC সমদ্বিবাহু।
প্রমাণ: ∆BMF আৰু ∆CMD ৰ
BM = CM [দিয়া আছে]
MF = MD [দিয়া আছে]
∠BFM = ∠CDM [প্রত্যেকেই সমকোণ]
∴ ∆BMF ≌ ∆CMD [RHS]
∴ ∠B = ∠C [C.P.C.T]
∴ ∆ABC সমদ্বিবাহু ত্রিভুজ।

উত্তৰঃ

11. চিত্রত ∆ABC ৰ BD আৰু CE দুডাল উন্নতি যাতে BD = CE,

(i) ∆CBD আৰু ∆BCE ৰ সমান অংশ তিনিটা লিখা।
(ii) ∆CBD = ∆BCE হ’বনে?
(iii) ∠DCB = ∠EBC হ’বনে? যদি নহয় কিয়?
উত্তৰঃ চিত্রত ∆ABC ৰ BD আৰু CE দুডাল উন্নতি।
BD = CE
এতিয়া, ∆CBD আৰু ∆BCE ত
BD = CE
BC সাধাৰণ বাহু
∠CDB – ∠CEB [প্রত্যেকেই 90°]
∴ ∆CBD ≌ ∆BCE [R.H.S]
∠DCB = ∠EBC [C.P.C.T.]
উত্তৰঃ

AC সাধাৰণ বাহু
∴ ∆ABC ≌ ∆CDA [বাহু – বাহু – বাহুস্বীকার্য]
অনুশীলনী – 7.2 |
|---|
তলৰ উক্তিবোৰৰ কোনটো সত্য–
1. ∆ABC আৰু ∆PQR ৰ AB = 4cm, BC = 5cm, AC = 6cm, PQ = 4cm, QR = 6cm, PR = 6cm তেন্তে তলৰ কোনটো সত্য।
(a) ∆ΑΒC = ∆QRP
(b) ∆АВС = ∆PQR
(c) ∆АВС = ∆PRQ
(d) ∆ΑΒC = ∆QPR
উত্তৰঃ (b) ∆АВС = ∆PQR
![]()
(a) ∠B= ∠C = 60°
(b) ∠B = ∠C = 30°
(c) ∠B = ∠C = 45°
(d) ∠B = ∠B = 50°
উত্তৰঃ (c) ∠B = ∠C = 45°
3. সমবাহু ত্রিভুজৰ প্ৰতিটো কোণৰ জোখ–
(a) 60°
(b) 30°
(c) 45°
(d) 40°
উত্তৰঃ (a) 60°
4. চিত্রত AB = CD, AD = CB আৰু ∠DAB = ∠BCD
(a) ∆ΑΒC ≌ ∆ADC
(b) ∆АВС ≌ ∆ACD
(c) ∆BAD ≌ ∆DCB
(d) ∆ΑΒC ≌ CAD
উত্তৰঃ (c) ∆BAD ≌ ∆DCB
5. ∆ABC আৰু ∆PQR ৰ AB = 3.5 চে.মি., BC = 7.1 চে.মি., AC = 5 চে.মি., PQ = 7.1 চে.মি., QR = 5 চে.মি. আৰু PR = 3.5 চে.মি. তেন্তে তলৰ কোনটো সত্য?
(a) ∆АВС ≌ ∆QRP
(b) ∆ΑΒC ≌ ∆PQR
(c) ∆ABC ≌ ∆RPO
(d) ∆ΑΒΟ ≌ ∆OPR
উত্তৰঃ (c) ∆ABC ≌ ∆RPO
6. ∆ABC আৰু ∆DEF ৰ AB = 7 চে.মি., BC = 5 চে.মি., ∠B = 50°, DE = 5 চে.মি., EF = 7cm, ∠E = 50° ৰ মধ্যবর্তী কোণ– কি চর্তত ত্রিভুজ দুটা সর্বাংগসম?
(a) SAS.
(b) RHS.
(c) ASA.
(d) SSS.
উত্তৰঃ (a) SAS.
7. ∆ABC আৰু ∆PQR ৰ ∠B = ∠P = 90° আৰু AB = RP। ত্রিভুজ দুটা সর্বাংগসম হ’ব যদি।
(a) AC = RQ
(b) ∠A = ∠P
(c) BC = QR
(d) ∠R = ∠C
উত্তৰঃ (a) AC = RQ
৪. যদি ∆ABC ≌ ∆DEF আৰু ∠A = 50°, ∠E = 85° তেন্তে ∠C = ?
(a) 50°
(b) 45°
(c) 85°
(d) 40°
উত্তৰঃ (b) 45°
Get Free NCERT PDFs
If you want to download free PDFs of any chapter, click the link below and join our WhatsApp group:

